ПрактикумКМ / ПрактикумКМ5

Практическое занятие № 5

Тема

Моделирование поведения динамических объектов в Simulink

Цель

Получение навыков создания моделей в системе моделирования Simulink

Построение и исследование моделей физических, динамических объектов

Разработка и исследование модели полета тела, брошенного с начальной скоростью под углом к горизонту

Краткие теоретические сведения

Предположим, что наблюдатель, находясь над уровнем земли на высоте одного метра, бросил камень под углом 30 градусов к горизонту с начальной скоростью 20 м/сек. Необходимо реализовать траектории полета камня под действием силы тяжести и определить расстояние от наблюдателя до точки падения камня. Влиянием атмосферы на полет камня пренебречь.

У

равнения движения камня, как это следует из школьного курса физики, имеют вид:

где 1 м, v = 20 м/сек, , 9, 81 м/сек.

На рис.1. дана структурная модель траектории полета камня.

Рис. 1 — Структурная схема модели траектории камня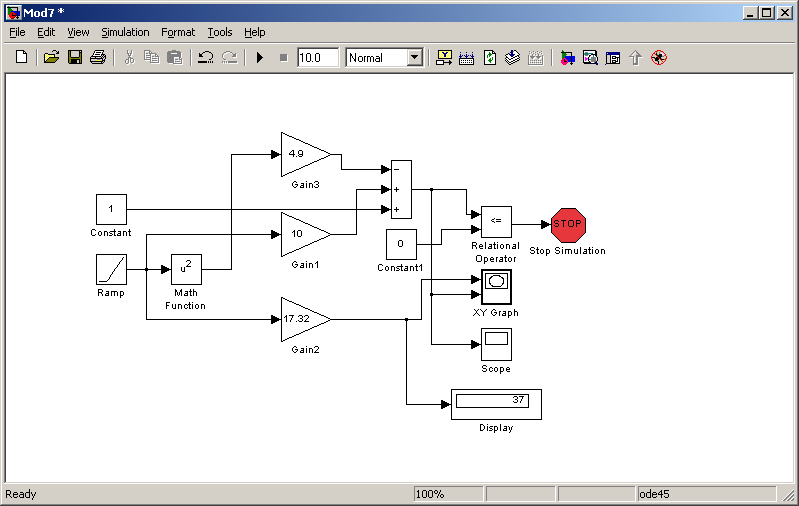

Значение текущей высоты полета камня формируется на выходе сумматора. Длина пути, пройденного камнем до встречи с землей, формируется на выходе блока Gain2. Входной сигнал ( t ) формируется блоком Ramp. Сигнал окончания моделирования формируется блоками Relational Operator и Stop Simulation, в момент времени, когда высота y сравняется с нулем, т.е. камень достигнет земли.

На рис. 2 и 3 показаны соответственно траектория камня на экране виртуального двухкоординатного регистратора (блок XY Gaph) и график изменения во времени высоты полета камня.

Рис. 2 — Траектория камня на экране двухкоординатного регистратора

Рис. 3 — График изменения во времени высоты полета камня

Цифровой регистратор Display отображает решение задачи: “Расстояние от наблюдателя до точки падения камня на землю» - 37 м.

Описание используемых блоков

Графопостроитель ХУ Graph

Назначение: Строит график одного сигнала в функции другого (график вида Y(X)).

Параметры:

x-min – минимальное значение сигнала по оси X.

x-max – максимальное значение сигнала по оси X

y-min – минимальное значение сигнала по оси Y.

y-max –максимальное значение сигнала по оси Y

Sample time – шаг модельного времени.

Блок имеет два входа: верхний вход предназначен для подачи сигнала, который является аргументом (X), нижний – для подачи значений функции (Y).

Графопостроитель можно использовать и для построения временных зависимостей. Для этого на первый вход следует подать временной сигнал с выхода блока Clock.

Блок остановки моделирования Stop Simulation

Назначение: Обеспечивает завершение расчета, если входной сигнал блока становится не равным нулю.

Параметры:

Нет.

При подаче на вход блока ненулевого сигнала Simulink выполняет текущий шаг расчета, а затем останавливает моделирование. Если на вход блока подан векторный сигнал, то для остановки расчета достаточно, чтобы один элемент вектора стал ненулевым.

Блок вычисления операции отношения Relational Operator

Назначение: Блок сравнивает текущие значения входных сигналов.

Параметры:

Relational Operator – тип операции отношения (выбирается из списка):

• = = - тождественно равно.

• ~ = - не равно.

• < - меньше.

• < = - меньше или равно.

• > = - больше или равно.

• > - больше.

В операции отношения первым операндом является сигнал, подаваемый на первый (верхний) вход блока, а вторым операндом сигнал, подаваемый на второй (нижний) вход. Выходным сигналом блока является 1, если результат вычисления операции отношения есть “ИСТИНА” и 0, если результат – “ЛОЖЬ”. Входные сигналы блока могут быть скалярными, векторными или матричными. Если оба входных сигнала – векторы или матрицы, то блок выполняет поэлементную операцию сравнения, при этом размерность входных сигналов должна совпадать. Если один из входных сигналов – вектор или матрица, а другой входной сигнал – скаляр, то блок выполняет сравнение скалярного входного сигнала с каждым элементом массива. Размерность выходного сигнала, в этом случае, будет определяться размерностью векторного или матричного сигнала, подаваемого на один из входов. Для операций = = (тождественно равно) и ~ = (не равно) допускается использовать комплексные входные сигналы. Входные сигналы также могут быть логического типа (boolean).

Варианты заданий

Задание формулируется следующим образом: «Выполнить моделирование поведения тела, брошенного с начальной скоростью под углом к горизонту. Определить для каждого из десяти значений начальной скорости из заданного в варианте интервала, оптимальный угол бросания камня по критерию максимального значения расстояния от точки падения тела до наблюдателя».

Вариант 1. Скоростьv = 5 — 6 м/сек.

Вариант 2. Скоростьv = 6 — 7 м/сек.

Вариант 3. Скоростьv = 7 — 8 м/сек.

Вариант 4. Скоростьv = 8 — 9 м/сек.

Вариант 5. Скоростьv = 9 — 10 м/сек.

Вариант 6. Скоростьv = 10 — 11 м/сек.

Вариант 7. Скоростьv =11 — 12 м/сек.

Вариант 8. Скоростьv = 12 — 13 м/сек.

Вариант 9. Скоростьv = 13 — 14 м/сек.

Вариант 10. Скоростьv = 14 — 15 м/сек.

Вариант 11. Скоростьv = 15 — 16 м/сек.

Вариант 12. Скоростьv = 16 — 17 м/сек.

Вариант 13. Скоростьv = 17 — 18 м/сек.

Вариант 14. Скоростьv = 18 — 19 м/сек.

Порядок выполнения практического задания

1. Получите у преподавателя вариант задания.

2. Изучите теоретическую часть.

3. Изучите блоки XY Graph, Relational Operator, Stop Simulation.

4. Разработайте и отладьте в Simulink модель рис.1.

5. Модифицируйте модель на рис. 1 так, чтобы удобно было проводить исследования поведения тела, брошенного с начальной скоростью под углом к горизонту. Для этого введите в модель блоки, явно задающие значения скорости и угла бросания и внесите другие необходимые изменения.

6. Выполните расчеты на подготовленной модели и соберите данные, необходимые для подготовки отчета о проделанной работе. Для этого проведите десять серий экспериментов для каждого выбранного Вами значения скорости из заданного в варианте интервала. При зафиксированном значении скорости меняйте угол бросания с тем, чтобы удовлетворить критерий максимизации расстояния от точки падения тела до наблюдателя.

7. Оформите отчет о выполнении практического занятия.

8. Защитите отчет.

Содержание отчета о проделанной работе

1. Название и цель практического занятия.

2. Вариант задания.

3. Математическая модель задачи.

4. Окно с вычислительной моделью.

5. Окно с результатами моделирования.

6. Анализ результатов и выводы.

7. Использованная литература.

Литература

1. Васильев В.В., Симак Л.А., Рыбникова А.М. Математическое и компьютерное моделирование систем и процессов в среде MATLAB/SIMULINK: Учебное пособие.- Киев: Изд-во НАН Украины.-2008.- 91 с.

2. Терехин В.В. Моделирование в системе MATLAB. Часть 2. SIMULINK: Учебное пособие.-Новокузнецк: Изд-во Кузбассвузиздат, 2004.- 376 с.