
Практическое занятие № 4
Тема
Моделирование объектов математической логики в Simulink
Цель
Получение навыков работы с системой моделирования Simulink
Получение навыков создания моделей
Построение и исследование моделей объектов математической логики
Разработка и исследование модели сумматора арифметического устройства ЭВМ
Краткие теоретические сведения
Сумматор — это электронная логическая схема, выполняющая суммирование двоичных чисел. Этот узел интересен тем, что он лежит в основе арифметического устройства ЭВМ и иллюстрирует некоторые принципы выполнения вычислительных операций в компьютере.
Для простоты начнем с изучения логической структуры простейшего возможного устройства, являющегося звеном сумматора. Это устройство - полусумматор - реализует сложение двух одноразрядных двоичных чисел, которые обозначим А и В. В результате получается двухразрядное двоичное число. Его младшую цифру обозначим S, а старшую, которая при сложении многоразрядных чисел будет перенесена в старший разряд, через Co (от английских слов "Carry out" - "выходной перенос"). Для лучшего понимания происходящего вспомните правило типа "ноль пишем, один в уме". Таблица истинности полусумматора дана в таблице 1.
Таблица1 – Таблица истинности
полусумматора
|
A |
B |
S |
Co |
|
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
Из таблицы истинности полусумматора получим:
![]() — сигнал
суммы
, Co
=
— сигнал
суммы
, Co
=
![]() - сигнал
переноса.
- сигнал
переноса.
Эти выражения упрощению не поддаются. Это легко проверить перебором всех четырех возможных случаев сочетания значений А и В, составив таблицу истинности для полусумматора. Следовательно, перенос происходит с помощью функции И, а выработка сигнала суммы производится функцией «ИСКЛЮЧАЮЩЕЕ ИЛИ» (сложение по модулю два). На рисунке 1 показана таблица истинности функции «ИСКЛЮЧАЮЩЕЕ ИЛИ».
|
A |
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1 — Таблица истинности функции
«ИСКЛЮЧАЮЩЕЕ ИЛИ»
На рисунке 2 дана логическая схема полусумматора.

Рис. 2 — Логическая схема полусумматора
Сумматор в отличие от полусумматора должен воспринимать 3 входных сигнала: 2 слагаемых и сигнал переноса с предыдущего разряда. Для лучшего понимания сущности работы комбинационного сумматора, на рисунке 3 рассмотрены примеры суммирования двух одноразрядных двоичных чисел.
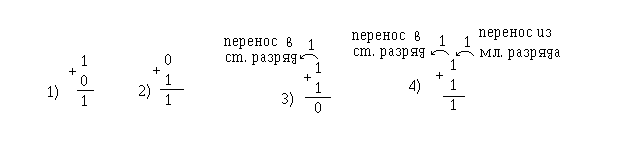
Рис. 3— Примеры суммирования двух
одноразрядных двоичных чисел
Полный одноразрядный (т.е. складывающий только одноразрядные двоичные числа) сумматор "умеет" при сложении двух цифр учитывать возможное наличие единицы, переносимой из старшего разряда (той, которая при обычном сложении столбиком остается "в уме". Обозначим этот "бит переноса" через Ci от английского "Carry in" - "входной перенос"). Таблица истинности для одноразрядного сумматора дана в таблице 2.
|
Таблица 2 — Таблица истинности для одноразрядного сумматора
|
||||||||||||||||||||||||||||||||||||||||||||||||||
При построении схемы сумматор удобно представить в виде двух полусумматоров, из которых первый суммирует разряды А и В, а второй к полученному результату прибавляет бит переноса Ci.
Заметим, что для суммирования младших разрядов чисел полусумматора уже достаточно, так как в этом случае отсутствует сигнал входного переноса.
Соединив два полусумматора и логическую
функцию ИЛИ (![]() ),
получим полный полусумматор, способный
осуществить сложение двух двоичных
разрядов с учетом возможности переноса
(рис. 4).
),
получим полный полусумматор, способный
осуществить сложение двух двоичных
разрядов с учетом возможности переноса
(рис. 4).

Рис.4 — Логическая схема одноразрядного
сумматора
Перейти к многоразрядным числам можно путем последовательного соединения соответствующего количества сумматоров. На рис. 4 представлена схема суммирования двух трехразрядных двоичных чисел А+B = S; в поразрядной записи эта операция имеет следующие обозначения: ( а3а2а1 ) + ( b3b2b1 ) = ( s4s3s2s1 ).

Рис.5 — Логическая схема сумматора
трехразрядных двоичных чисел
Последовательность логических схем на рисунке отражает важнейшую в современной цифровой электронике и вычислительной технике идею последовательной интеграции. Такая интеграция позволяет реализовать все более функционально сложные узлы современного компьютера.
