Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4629 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Санкт-Петербургский государственный университет информационных технологий, механики и оптики
Предмет:
Высшая математика
Файл:

Литература и лекции / Векторы

.pdf
Скачиваний:
0
Добавлен:
30.06.2023
Размер:
205.77 Кб
Скачать
☆

Замечание Если вектор параллелен заданной плоскости, то параллельным переносом, от

которого вектор не изменяется, вектор можно перенести на плоскость. Поэтому слова "вектор, параллельный заданной плоскости, или лежащий на ней" впредь, для краткости, будут заменяться словами "вектор, лежащий на заданной плоскости".

Определение Набор линейно независимых элементов

g1; g2; : : : ; gn 2 E образует базис

в линейном пространстве E ; åñëè 8x 2 E 9 набор чисел ¸1; ¸2; : : : ; ¸n такой, что x = ¸1g1 + ¸2g2 + : : : + ¸ngn : Количество элементов базиса n называется размерностью пространства E :

Замечание Множество векторов, лежащих на заданной прямой, есть линейное пространство.

Множество векторов, лежащих на заданной плоскости, есть линейное пространство. Множество векторов в окружающем нас 3 мерном пространстве есть линейное пространство.

Сказанное непосредственно вытекает из определния суммы векторов и определния произведения вектора на число.

Теорема о базисе на прямой

Базисом множества векторов, лежащих на заданной прямой, может служить любой íåнулевой вектор, лежащий на ней.

Доказательство

Пусть вектор ~g (ïðè÷¼ì, ~g 6= ~o) лежит на прямой `. Рассмотрим произволь-

ный вектор ~x, лежащий на прямой `. Åñëè ~x сонаправлен с ~g, òî ~x = jj~x~gjj ¢ ~g. Åñëè ~x антинаправлен с ~g, òî ~x = ¡jj~x~gjj ¢ ~g.

Теорема о базисе на плоскости

Базисом множества векторов, лежащих на заданной плоскости, может служить любая пара íåколлинеарных векторов, лежащих на ней.

11

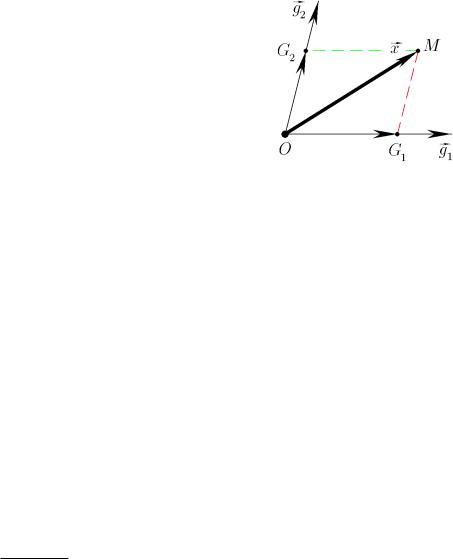
Доказательство

Пусть векторы ~g1 è ~g2 неколлинеарны.

Рассмотрим случай, когда ~x неколлинеарен векторам ~g1 è ~g2.

Отсутствие коллинеарности автоматически означает, что векторы ~x, ~g1, ~g2 âñå ненулевые.

Ðèñ. 4

Совместим начала векторов ~x, ~g1, ~g2 в точке O (Рис. 4). Пусть `1, `2 прямые, на которых лежат векторы ~g1, ~g2 соответственно. Пусть точка M есть конец вектора ~x. Провед¼м через не¼ две пунктирные прямые, параллельные прямым `1 è `2 (íà Рис. 3 показаны çåë¼íûì è красным цветом соответственно). Пусть G1, G2 точки

¡¡!

пересечения этих пунктирных прямых с `1 è `2. Тогда вектор AG1, лежащий на прямой

¡¡!

`1 ; может быть, согласно Теореме 1, представлен в виде AG1 = ¸1~g1. Аналогично

¡¡!

AG2 = ¸2~g2. По правилу параллелограмма

¡¡! ¡¡! ¡¡!

~x = OM = AG1 + AG2 = ¸1~g1 + ¸2~g2 ;

что и доказывает Теорему.

Теорема о базисе в тр¼хмерном пространстве

Базисом множества векторов в тр¼хмерном пространстве может служить любая тройка некомпланарных векторов.

Доказательство

Пусть векторы ~g1, ~g2 è ~g3 некомпланарны.

Доказательство построим только для случая, когда ~x неколлинеарен векторам ~g1, ~g2 è ~g3 , а также некомпланарен парам векторов f~g1; ~g2g, f~g1; ~g3g, f~g2; ~g3g.

12

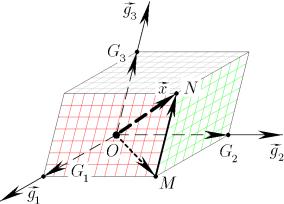
Ðèñ. 5

Совместим начала векторов ~x, ~g1, ~g2, ~g3 в точке O (Рис. 5). Пусть `1, `2, `3 прямые, на которых лежат векторы ~g1, ~g2, ~g3 соответственно. Пусть точка N есть конец вектора ~x.

Провед¼м через точку N плоскость, параллельную плоскости O~g2~g3 (íà Ðèñ. 5

показана красным цветом).

Провед¼м через точку N плоскость, параллельную плоскости O~g1~g3 (íà Ðèñ. 5

показана çåë¼íûì цветом).

Провед¼м через точку N плоскость, параллельную плоскости O~g1~g2 (íà Ðèñ. 5

показана голубым цветом).

Упомянутые три пары плоскостей лежат на гранях параллелепипеда ON. Пусть G1, G2, G3 точки пересечения цветных плоскостей с векторами ~g1, ~g2, ~g3

соответственно (точнее, с прямыми `1, `2, `3 соответственно).

Пусть M точка пересечения плоскости O~g1~g2 с красной и зел¼ной плоскостями.

¡¡! ¡¡! ¡¡!

ßñíî, ÷òî ON = OM + MN.

¡¡! ¡¡! ¡¡! ¡¡! ¡¡!

Векторы OG1, OG2, OG3, OM, а также ~x = ON "загорожены" цветными гра-

нями и поэтому показаны прерывистыми линиями.

¡¡!

Вектор OM находится на плоскости O~g1~g2 , следовательно, по Теореме о базисе

¡¡!

на плоскости, существуют числа ¸1, ¸2 такие, что OM = ¸1~g1 + ¸2~g2.

¡¡!

Вектор OG3 находится на одной прямой с вектором ~g3 , следовательно, по Тео-

¡¡!

реме о базисе на прямой, существует число ¸3 такое, что OG3 = ¸3~g3.

¡¡! ¡¡!

Заметим, что MN = OG3, поскольку MN è OG3 являются параллельными

13

р¼брами параллелепипеда.

По правилу треугольника

~x =

¡¡!

=

¡¡!

+

¡¡!

= ( 1 1 +

2 2) +

¡¡!3 =

1 1 +

2 2 +

3 3

 

ON

 

OM

 

MN

¸ ~g

¸ ~g

OG

¸ ~g

¸ ~g

¸ ~g ;

что и доказывает Теорему.

Определение

Ось это прямая, на которой выбрано направление, называемое положительным. Противоположное направление считается отрицательным. Числовая ось это ось, на которой выбрана точка, называемая началом

отсч¼та (чаще всего она обозначается буквой O "Origin"), а также вы-

бран масштаб отсч¼та.

Каждой точке на числовой оси ставится в соответствие число (численное выражение точки на оси), модуль которого выражает расстояние этой точ- ки от начала отсч¼та, прич¼м, число бер¼тся со знаком "плюс", если точка отстоит от начала в положительном направлении оси, и со знаком "минус"в противоположном случае.

Замечание При работе с векторами используются понятия "расстояние", "длина", поэтому

есть смысл далее совместно с векторами рассматривать только числовые оси.

Определение

Проекция точки на ось это основание перпендикуляра, опущенного из точки на ось.

Численное выражение проекции точки на ось это число, поставленное в соответствие проекции точки на ось.

Проекция вектора на ось это вектор с началом и концом соответственно в проекции начала и проекции конца вектора на ось.

Численное выражение проекции вектора на ось это разность численнного выражения проекции конца вектора на ось и численного выражения

14

проекции начала вектора на ось.

Компонента вектора по оси ` это численное выражение проекции вектора на ось `.

Определение Îðò îñè ` это единичный вектор, параллельный оси ` (или лежащий на

ней) и сонаправленный с ней.

Теорема

Перемещение вектора параллельным переносом не изменяет проекцию вектора на заданную ось.

Без доказательства. Замечание

Âлитературе применяется два способа написания проекции вектора ~a íà îñü `:

1.Pr` ~a.

2.Ïð` ~a.

От второго способа лучше воздержаться, так как использование русских букв в математических формулах признак дурного тона.

Теорема

1.

~

~

Pr` (~a + b) = Pr` ~a + Pr` b (проекция суммы есть сумма проекций).

2.

Pr` (¸¢~a) = ¸¢Pr` ~a

(числовой множитель выносится за знак проекции).

Без доказательства. Теорема

c ,

Pr` ~a = j~aj ¢ cos(~a `)

Без доказательства.

ãäå c

~a ` угол между вектором ~a è îñüþ `.

15

Определение Декартова прямоугольная система координат это пространственная си-

стема тр¼х попарно перпендикулярных числовых осей Ox, Oy, Oz, имеющих общее начало в точке O (Ðèñ 6).

Îðòû îñåé

 

,

 

,

 

принято обозначать через ~, ~

, ~

соответственно.

 

Ox

 

Oy

 

Oz

i j

k

 

Îñè Ox, Oy, Oz принято называть координатными.

Ðèñ. 6

Определение

Численные выражения проекций PrOx~a PrOy ~a PrOz ~a вектора ~a íà îñè Ox; Oy; Oz; принято обозначать соответственно как ax ; ay ; az ; и называть компонентами вектора ~a.

Часто применяется обозначение ~a = (ax ; ay ; az).

~a =

0 ay

1; íî îíî

Применяется, также, и более "высокое" обозначение

Компоненты в скобках разделены запятыми.

 

ax

C

чрезмерно "расходно" в отношении бумаги.

 

B az

 

 

@

A

Теорема

Справедливо равенство

~ ~ ~

~a = (ax ; ay ; az) = ax¢ i + ay ¢ j + az ¢ k :

Без доказательства.

16

Определение

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ãäå ~a~b

угол между векторами ~a è ~b.

j j¢j j¢cos(c)

 

 

 

 

 

 

 

 

 

 

 

 

, ~

~

~

 

Скалярным произведением векторов ~a b

называется число ~a b

~a b ,

 

 

 

c

 

 

~a ¢ b

 

 

(~a; b)

 

 

 

Обозначение:

~,

èëè

 

~

.

 

 

Замечание

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

~

~

 

Мы будем пользоваться обозначением ~c = ~a ¢ b,

èëè ~c = ~ab, которое предпочи-

тают физики и техники. Обозначение

 

~

 

 

~c = (~a; b) в чести у математиков теоретиков.

Замечание

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

~

 

~

 

 

~

 

Легко проверить, что ~a ¢ b = jbj ¢ Pr`~b ~a = j~aj ¢ Pr`~a b.

 

Теорема

о свойствах скалярного произведения векторов

 

1.

~a ¢ ~a = j~aj

2

¸ 0

,

ïðè÷¼ì,

 

 

~.

 

 

 

 

 

 

 

 

 

~a ¢ ~a = 0 () ~a = 0

 

2.

~

~

 

(коммутативность).

 

 

~a ¢ b = b ¢ ~a

 

 

3.

 

~

 

 

 

~

(ассоциативность).

 

(¸~a) ¢ b = ¸ ¢ (~a ¢ b)

 

4.

 

~

 

 

 

 

~

 

(дистрибутивность).

 

(~a + b) ¢ ~c = ~a ¢ ~c + b ¢ ~c

 

Без доказательства.

Замечание

То, что используется в Пункте 1, принято называть "скалярное произведение вектора на себя".

Теорема (признак перпендикулярности векторов)

Пусть

Тогда

~

~

~

~a 6= 0 ;

b 6= 0 :

~

 

~

~a ? b

() ~a ¢ b = 0 :

Доказательство необходимости

~

 

~

 

¼

~a ? b

=)

c

=

2

 

 

~a b

 

 

~ ~

=) ~a ¢ b = j~aj ¢ jbj

 

 

~

 

~

 

0 = 0 :

¢

cos(~a b) = ~a

j ¢ j

b

j ¢

 

 

=0c

j

 

 

 

|

 

{z

 

}

 

 

 

 

 

17

Доказательство достаточности

 

¢

~

 

=) j

 

j ¢ j

~

~

~

~

 

¼

 

~a

b

= 0

~a

b

~a b

~a b

~a b

2

:

 

 

6=~0

6=~0

j ¢ cos(c) = 0

=) cos(c) = 0 =)

c

=

 

 

 

 

 

 

|{z}

 

|{z}

 

 

 

 

 

 

Теорема

 

о вычислении скалярного произведения векторов в декартовых компонентах

 

 

Åñëè

 

 

 

 

 

, ~

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

~a = (ax; ay; az)

 

b = (bx; by; bz),

 

 

 

 

 

 

 

 

 

 

 

 

 

 

~

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

òî ~a ¢ b = axbx + ayby + azbz .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Доказательство

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

~ ~

~ ~

,

~ ~

 

~

 

~

 

 

,

 

~

 

~

 

~

~

 

 

 

 

,

 

так как в этих равенствах

i ¢ j = j ¢ i = 0 i ¢ k = k ¢ i = 0

 

j ¢ k = k ¢ j = 0

 

 

 

 

 

участвуют скалярные произведения взаимно перпендикулярных векторов.

~ ~

 

, ~

~

 

, ~

~

 

 

 

, так как в этих равенствах участвуют скалярные

i ¢ i = 1

j ¢ j = 1

k ¢ k = 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

произведения единичных векторов на себя.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

~

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

~

 

~

 

 

~

 

 

 

~

~

~

~a ¢ b = (ax; ay; az) ¢ (bx; by; bz) = (axi + ayj + azk) ¢ (bxi + byj + bzk) =

 

 

 

 

 

 

 

 

~

 

~

 

 

 

 

 

 

 

~

~

 

 

 

 

 

~

 

~

 

 

 

 

 

 

 

= axbx ¢ i ¢ i + axby ¢ i ¢ j + axbz ¢ i ¢ k +

 

 

 

 

 

 

 

+ aybx

 

|{z} + y

 

y

 

|{z} +

 

y z

 

 

|{z}+

 

 

 

 

 

 

 

 

 

 

=1

 

 

 

 

 

 

 

 

=0

 

 

 

 

 

 

=0

 

 

 

 

 

 

 

 

 

¢

~

¢

~

 

a b

 

¢

~

¢

~

a b

 

¢

~

¢

~

 

 

 

 

 

 

 

 

 

j

i

 

 

j

j

 

 

j

k

 

 

 

 

 

 

 

 

 

 

|{z}

 

 

 

 

 

 

 

|{z}

 

 

 

 

|{z}

 

 

 

 

 

 

 

 

 

 

=0

 

 

 

 

 

 

 

=1

 

 

 

 

 

=0

 

 

~ ~

~ ~

+ azbx ¢ k ¢ i + azby ¢ k ¢ j + azbz

|{z}

=0

=0

|{z}

 

~~

¢k ¢ k =

|{z}

=1

= axbx + ayby + azbz :

Доказательство закончено.

Определение

 

 

 

 

 

 

 

 

 

 

 

 

 

 

,

~

 

 

 

Векторным произведением векторов ~a

b называется вектор ~c, который

подчиняется требованиям:

 

 

 

 

 

1.

~

 

 

 

 

 

 

 

~c ? ~a, ~c ? b.

c

c

 

 

 

è ~

 

 

~

 

 

 

2.

~

~

 

 

 

j~cj = j~aj¢jbj¢j sin(~a b)j, ~a b кратчайший угол между векторами ~a

b :

3.

Направление вектора

~c

таково, что если смотреть со стороны острия

вектора ~c на векторы ~a

,

~

 

äî

~

 

 

b, то движение от ~a

 

b по кратчайшему

18

углу производится против часовой стрелки.

~

~

Обозначение: ~c = ~a £ b,

èëè ~c = [~a; b].

Замечание

 

 

~

Мы будем пользоваться обозначением ~c = ~a £b, которое предпочитают физики

~

в чести у математиков теоретиков.

и техники. Обозначение ~c = [~a; b]

Замечание

 

Если вектор ~c подчиняется только требованиям 1 и 2, то вектор ¡~c также

им подчиняется, то есть требований 1 и 2 недостаточно для однозначного определения вектора ~c.

Если вектор

~c

подчиняется требованию 3, то принято говорить, что тройка

векторов ~a

,

~

 

правая. Название "правая" сложилось потому, что такая тройка

 

b, ~c

векторов похожа на конфигурацию указательного (~a

), среднего (~

b) и большого (~c)

пальцев правой руки.

Если тройка векторов не является правой, то она называется левой тройкой.

Теорема

(признак коллинеарности векторов)

 

 

 

 

Пусть

~

~

~

 

 

 

 

 

~a 6= 0 ;

b 6= 0 :

 

 

Тогда

~

()

 

~

~

 

 

 

~a jj b

 

~a £ b = 0 :

 

Доказательство необходимости

 

 

 

~

то векторы

~

параллельны одной прямой. Это означает, что

Åñëè ~a jj b ;

~a ; b

Íî sin(0) = sin(¼) = 0 ; значит,

c

c

векторы либо сонаправлены, тогда

~

~

~a b = 0 ;

ëèáî антинаправлены, тогда ~a b = ¼ :

sin(c) = 0

=) j

£

 

j = j

j ¢ j j ¢

 

 

=0c

j

j ¢ j j ¢

)

~

~a

 

~

~a

~

~

 

~

=

~a b

 

b

b

sin(~a b) = ~a

b 0 = 0

 

 

 

 

 

 

|

 

{z

 

}

 

 

 

Доказательство достаточности

~ ~

~a £ b = 0 :

~ ~ ~

~a £ b = 0 =) j~a £ bj = 0

=) j

~a

j ¢ j

~

~

b

~a b

6=~0

6=~0

j ¢ sin(c) = 0 =)

 

|{z}

 

|{z}

 

c

~

sin(~a b) = 0 :

19

~

 

 

 

 

 

è ~

~a b кратчайший угол между векторами ~a

 

b ; синус кратчайшего угла может быть

равен нулю только при

~

~

 

а оба эти случая означают, что векторы

~a b = 0 èëè ~a b = ¼;

c

 

прямой, значит, они коллинеарны.

параллельны одной

 

c

c

 

 

Теорема

о свойствах векторного произведения векторов

 

1.

 

~

(векторное произведение вектора на себя нулевой вектор).

 

 

~a £~a = 0

 

 

 

 

2.

~

 

~

(антикоммутативность).

~a £ b = ¡b £ ~a

3.

 

~

 

~

 

 

(¸~a) £ b = ¸ ¢ (~a £ b) (ассоциативность).

4.

~

 

 

~

 

 

(~a + b) £ ~c = ~a £ ~c + b £ ~c (дистрибутивность).

Без доказательства.

Теорема о вычислении векторного произведения векторов в декартовых компонентах

, ~

Åñëè ~a = (ax; ay; az) b = (bx; by; bz),

òî ~a ~b =

¯aix

ay

£

¯

~

~

 

¯

 

j

 

 

 

 

¯

 

 

 

¯

 

 

 

¯

 

by

 

¯ bx

az ¯

= ay

~

¯

 

k

¯ by

bz

¯

¯

 

¯

¯

 

¯

¯

 

¯

 

 

¯

 

bz

¯

¢~i ¡

¯ bx

bz

¯

¢~j +

¯ bx

by

¯

¢ ~k :

az

¯

 

¯

ax

az

¯

 

¯

ax

ay

¯

 

 

¯

 

¯

 

 

¯

 

¯

 

 

¯

 

 

¯

 

¯

 

 

¯

 

¯

 

 

¯

 

Доказательство.

так как в этом равенстве требования 1, 2, 3 для векторного произве-

~

~

~,

i £ j = k

 

 

 

 

 

дения выполнены. ~

~

~

по свойству 1.

~

~

~,

j £ i = ¡k

 

 

так как в этом равенстве требования 1, 2, 3 для векторного произве-

j £ k = i

 

 

 

 

 

дения выполнены. ~

~

~

по свойству 1.

~

~

~,

k £ j = ¡i

 

 

так как в этом равенстве требования 1, 2, 3 для векторного произве-

k £ i = j

 

 

 

 

 

дения выполнены. ~

~

~

по свойству 1.

 

 

~,

i £ k = ¡j

 

 

~

~

~ ~

 

~, ~

~

~, векторное произведение вектора на себя есть

i £ i = 0

j £ j = 0 k £ k = 0

нулевой вектор.

~

~

~

~

~

~a £ b = (ax; ay; az) £ (bx; by; bz) = (axi + ayj + azk) £ (bxi

~ ~

~

~

~

~

= axbx ¢ i £ i + axby ¢ i £ j + axbz ¢ i £ k +

|{z}

|{z}

|{z}

~

~

 

 

~

=0

=k

 

 

=¡j

~~

+byj + bzk) =

20

Соседние файлы в папке Литература и лекции
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности