Физика. Теоретические курсы / Ландсберг Г.С. Элементарный учебник физики / Ландсберг Г.С. Элементарный учебник физики. Том 3

вая природа света долго ускользала от внимания исследователей.

Как уже говорилось ранее, в опытах по фотоэффекту на проводниках было обнаружено, что максимальная кинетическая энергия электронов, вылетающих под действием света (так называемых фотоэлектронов), связана с работой выхода A и частотой облучающих проводник электромагнитных волн соотношением

Это соотношение в 1916 г. было подтверждено американским физиком Р. Милликеном. Тонкие и тщательные измерения Милликена, выполненные по схеме опытов, описанных в § 183, позволили установить линейную зависимость между максимальной энергией, получаемой электроном от света, и частотой этого света, определить универсальный характер постоянной Планка h и измерить эту величину (h = 6,6 · 10−34 Дж · с). В дальнейших опытах частота падающего на поверхность металла излучения изменялась в широких пределах — от видимого света до рентгеновского и во всем исследованном интервале частот результаты измерений оказались в превосходном согласии с теорией.

Вэкспериментах с рентгеновским излучением представления

оквантах были подвергнуты особенно тщательной и разносторонней проверке. Действительно, кванты видимого света (фото-

ны) обладают очень малой энергией — так, для желтого света ν ≈ 5 · 1014 с−1 и hν ≈ 3,31 · 10−19 Дж. Поэтому для регистра-

ции такого света в большинстве опытов приходится иметь дело

сбольшим числом фотонов в единицу времени. В соответствии

сэтим, действие, производимое летящими по всем направлениям световыми квантами, распределенными случайным образом, трудно отличить от действия волны, равномерно распространяющейся во все стороны. Чем больше энергия квантов, тем легче наблюдать действие отдельного кванта и легче, следовательно, осуществить опыт по наблюдению распространения энергии излучения не во все стороны равномерно, а вспышками то по одному, то по другому направлению. Энергия фотонов в рентгеновской области спектра значительно превышает энергию фотонов видимого света. Кроме того, в опытах с рентгеновским излучением легче осуществить условия для испускания небольшого числа квантов в единицу времени.

Для получения рентгеновского излучения нужно бомбардировать электронами анод рентгеновской трубки (см. §§ 151, 153). Всякая остановка (торможение) электронов в веществе анода

502 Гл. XXII. Строение атома

сопровождается испусканием рентгеновского излучения. Теория световых квантов предсказывает, что в самом благоприятном случае вся кинетическая энергия электрона после его остановки перейдет полностью в один-единственный фотон, энергия которого hν определяется из условия Wкин = hνmax. Если электрон разгонялся разностью потенциалов U , то Wкин = eU .

Итак, максимальная частота рентгеновского излучения зада-

Действительно, измерения подтвердили, что рентгеновский спектр в таких экспериментах характеризуется коротковолновой

границей

λmin = c/νmax,

где c — скорость света, а максимальная частота излучения согласуется с условием (209.2). Более короткие волны (большие значения частоты ν) никогда при этом не наблюдаются, а более длинные волны соответствуют превращению лишь части кинетической энергии электрона в рентгеновское излучение. Определение коротковолновой границы рентгеновского спектра может быть выполнено весьма надежно. Поэтому такие опыты использовались для определения значения постоянной Планка (в соответствии с (209.2)). Наилучшие измерения, выполненные этим методом, дали h = 6,624 · 10−34 Дж · с 1). Эти данные согласуются с результатами измерения h в опытах по фотоэффекту. Таким образом, теория квантов хорошо подтверждается не только опытами по поглощению энергии излучения (фотоэффект), но и опытами по ее испусканию.

Регулируя число электронов, бомбардирующих анод рентгеновской трубки, мы можем изменять число излучаемых рентгеновских фотонов. Если теперь подвергнуть металлическую пластинку воздействию рентгеновским излучением, вызывая тем самым выход фотоэлектронов, то, как показывают опыты, кинетическая энергия этих электронов будет равняться энергии рентгеновских квантов (так как энергия электронов и рентгеновских квантов в таких опытах составляет десятки киловольт, то работой выхода электронов из металла — несколько электронвольт — можно пренебречь).

Таким образом, весь цикл превращений энергии в этих опытах выглядит так: 1) превращение работы электрического по-

1) Наиболее точное современное значение постоянной Планка h = = (6,626176 ± 0,000036) · 10−34 Дж · с.

ля eU в кинетическую энергию электрона W = 1/2mve2 в рентгеновской трубке; 2) превращение кинетической энергии электрона в энергию излучаемого электроном при резком торможении рентгеновского кванта; 3) поглощение фотона электроном и превращение его энергии в кинетическую энергию фотоэлектрона:

eU = 12mve2 = hν = 12mv2.

Такие опыты можно сильно разнообразить, пользуясь удобными условиями экспериментов с рентгеновским излучением. Все они показывают, что энергия передается в этих явлениях концентрированными порциями, а не накапливается постепенно, как это имело бы место при непрерывной передаче энергии

ввиде электромагнитной волны. Один из самых убедительных опытов такого типа был поставлен Абрамом Федоровичем Иоффе (1880–1960). Были выполнены также прямые эксперименты по регистрации отдельных фотонов, показывающие, что энергия рентгеновского излучения распространяется от анода трубки

вразные стороны не одновременно, а в виде порций (квантов), летящих то в ту, то в другую сторону.

Таким образом, исследование фотоэффекта и опыты с рентгеновским излучением убедительно показали, что свет ведет себя

вэтих явлениях не как волна, а как некоторая частица — фотон, которая образуется при излучении, летит в каком-то направлении и, поглощаясь, целиком отдает свою энергию другой частице. Но если фотон ведет себя как частица с полной энергией W = hν, то он должен иметь и определенный импульс. Фотон имеет скорость, равную скорости света. Поэтому из общих формул релятивистской механики (см. §§ 199, 200) следует ожидать, что он будет обладать импульсом

Как мы уже видели раньше (§ 200), отличительной особенностью фотона является равенство нулю его массы покоя: фотон всегда движется со скоростью света и не может существовать как покоящаяся частица.

То, что фотоны обладают импульсом, косвенным образом следует уже из опытов по световому давлению (§ 65). Способность света оказывать давление на отражающую или поглощающую поверхность следует интерпретировать как результат передачи импульса фотонов, подобно тому как отражающиеся от стенки

сосуда молекулы газа, передавая ей импульс, оказывают на нее давление (см. том I).

Очень важную роль в развитии представлений о фотонах как некоторых элементарных частицах сыграли опыты американского физика Артура Комптона (1892–1962), в которых непосредственно было показано, что фотоны при соударениях с электронами ведут себя, как частицы с энергией и импульсом, связанными между собой соотношением (209.3).

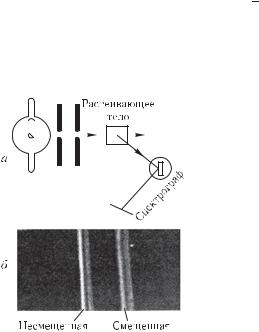
Исследуя рассеяние рентгеновского излучения в веществе из легких атомов (рис. 371), Комптон в 1923 г. обнаружил, что при этом происходит изменение длины волны рентгеновского излучения, и установил связь между изменением длины волны λ и углом рассеяния θ:

Здесь постоянная λ0 = h/mec = 2,43 · 10−12 м была первоначально определена из опыта. Результаты этих опытов противоречат классическим представлениям о рассеянии электромагнитных

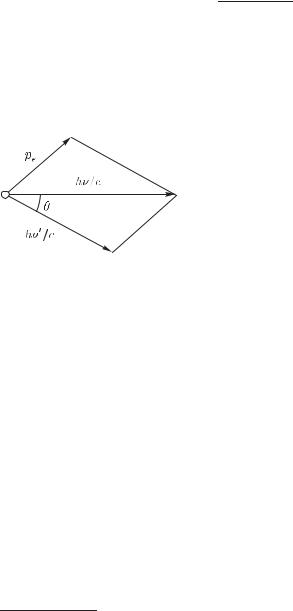
ным электроном (а не с атомом как целым), напоминающее соударение упругих шаров. Применяя законы сохранения энергии

и позитрон (частица, имеющая массу электрона и положительный заряд, равный по абсолютной величине заряду электрона), причем ядро остается при этом без изменений (см. § 223). В этих опытах было доказано, что электроны и позитроны не выделяются из ядра, ибо ядро остается неизменным, а возникают под действием света. Разлетевшиеся электрон, позитрон и ядро обладают энергиями и импульсами, которые они заимствуют у исчезнувшего фотона.

Был обнаружен и обратный процесс, когда электрон и позитрон, взаимодействуя друг с другом, перестают существовать как элементарные заряженные частицы: их заряды взаимно нейтрализуются, а их энергии покоя переходят в энергию образующейся

втаком процессе пары фотонов, разлетающихся со скоростью света.

Как мы увидим в дальнейшем (гл. XXV), такие взаимные превращения одних частиц в другие являются очень важным и характерным их свойством, и в этом смысле фотон ничем не отличается от других микрочастиц, таких, как электроны, протоны и т. д.

Наконец, следует сказать, что фотоны, как и все другие частицы, могут испытывать на себе действие гравитационного поля. Так, точные наблюдения во время полных солнечных затмений за положением звезд, свет от которых проходит вблизи Солнца, показывают, что этот свет подвергается притяжению Солнца и отклоняется от своего первоначального пути. Качественно это можно понять, если учесть, что фотоны об-

ладают энергией hν, которой соответствует «масса движения» m = hν/c2, испытывающая гравитационное притяжение к Солнцу. Другой экспериментально наблюдавшийся очень красивый эффект состоит в том, что фотон, двигаясь в гравитацион-

ном поле, изменяет свою энергию. При этом энергия фотона W = mc2 = hν при движении, например, в поле тяготения Земли, меняется, вследствие изменения его потенциальной энергии

вэтом поле, на величину

mgH = hν gH, c2

где H — путь, который пролетает фотон вдоль направления гравитационного поля Земли. Отсюда можно заключить, что частота фотона изменяется на величину

ν = νgH . c2

В опытах, в которых исследовалось движение фотонов, испускаемых возбужденными ядрами атома, в поле тяготения с высоты H = 22,6 м до уровня поверхности Земли, удалось наблюдать изменение частоты фотонов, которое прекрасно совпало с теоретическими предсказаниями:

подтвердив тем самым, что фотоны подвержены гравитационному воздействию.

Таким образом, как мы смогли убедиться, рассмотрев многочисленные и разнообразные эксперименты, в ряде случаев свет надо рассматривать как поток корпускул — фотонов, обладающих свойствами, присущими другим микрочастицам. Однако для объяснения таких явлений, как интерференция и дифракция, приходится исходить из волновых свойств электромагнитного излучения. Оба аспекта природы — и волновой и корпускулярный — оказываются одинаково существенными. Поэтому для объяснения всех особенностей поведения излучения оказалось необходимым признать, что электромагнитные волны в известных условиях проявляют свойства потоков частиц. С равным правом можно высказать и обратное утверждение: частицы электромагнитного поля — фотоны — проявляют волновые свойства. Такой корпускулярно-волновой дуализм (двойственность) фотонов противоречит сложившимся классическим, обособленным друг от друга представлениям о волнах и частицах.

Сначала казалось, что фотоны, обладающие этими необычными свойствами, существенно отличаются от других частиц, например от электронов или протонов. Однако дальнейшее развитие физики микромира позволило установить, что корпуску- лярно-волновой дуализм отнюдь не является специфической особенностью фотонов, а имеет гораздо более общий характер.

§ 210. Понятие о квантовой (волновой) механике. Изучение строения атома привело к выводу, что поведение электронов

ватоме, так же как поведение фотонов, противоречит привычным законам классической физики, т. е. законам, установленным

вопытах с телами макроскопических размеров. Существование дискретных уровней энергии электронной оболочки атома, закономерности переходов между уровнями и заполнения этих энергетических состояний невозможно было объяснить, пользуясь обычными представлениями механики и законами электромагнетизма.

Важный шаг в разъяснении этих противоречий был сделан в 1923 г. французским физиком Луи де Бройлем (р. 1892). Он выдвинул и обосновал предположение о том, что не только фотоны, но и любые частицы обладают волновыми свойствами, которые не учитываются классическими законами, но играют существенную роль в атомных явлениях.

Кванты электромагнитного излучения — фотоны, как мы видели выше, характеризуются импульсом p = hν/c. Вместе с тем световая волна с частотой ν имеет длину λ = c/ν. Исключая из этих выражений частоту, получаем связь между длиной волны и импульсом фотона

Если в самом деле, в рамках представления о корпускуляр- но-волновом дуализме, свойства фотонов и других частиц подобны друг другу, то это соотношение должно быть применимо теперь к любым частицам. Таким образом, была получена формула для длины волны де Бройля, т. е. для длины волны, которую следует сопоставить частице с импульсом p, чтобы описать ее волновые свойства. Эта формула также имеет вид (210.1). Если скорость частицы с массой покоя m мала по сравнению со скоростью света, то формула для длины волны де Бройля примет вид

Для проверки справедливости гипотезы де Бройля были произведены опыты по рассеянию электронов на кристаллах.

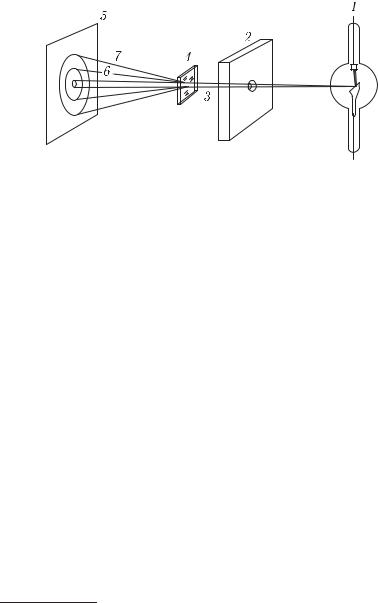
В свое время рассеяние рентгеновского излучения на кристаллах было использовано для доказательства их волновой природы (см. § 154). Благодаря интерференции вторичных волн, испускаемых правильно расположенными атомами кристалла, рассеяние происходит не в любых направлениях, а только под некоторыми определенными углами к падающему пучку. На фотопленке, расположенной позади рассеивающего кристалла (рис. 373), помимо центрального пятна от прямого пучка, получается система пятен от рассеянного (дифрагированного) излучения. Пример такого снимка приведен на рис. 374, а 1).

1) На рис. 374 изображены картины, получаемые с поликристаллическим образцом, т. е. образцом, состоящим из большого числа мелких, беспорядочно ориентированных кристалликов. При таком образце отдельные пятна от рассеянного излучения сливаются в окружности, окаймляющие центральный пучок.

Иначе обстоит дело с электронами или атомами, массы которых несравненно меньше микрограмма. При не слишком большой скорости им соответствует длина волны того же порядка, что

Рис. 374. Фотоснимки дифракции рентгеновского излучения (а)

иэлектронов (б) на поликристаллическом золоте

идлины волн рентгеновского излучения. Так, для атома гелия с энергией 0,04 эВ (энергия теплового движения при комнатной

температуре) λ = 0,7 · 10−10 м; для электрона с энергией 13,5 эВ λ = 3,3 · 10−10 м.

Из оптики мы знаем, что волновой характер света проявляется весьма отчетливо в тех случаях, когда длины волн сравнимы с размерами тел, с которыми свет взаимодействует. Так, при прохождении света через отверстие размером в несколько длин волн или при отражении от дифракционной решетки с малым расстоянием между штрихами и т. д. нельзя не учитывать волновых свойств света. Напротив, при прохождении света через окно квартиры или при отражении от зеркала с редкими царапинами дифракционные явления можно не принимать во внимание; они практически незаметны. Точно так же волновые свойства частиц имеют значение только тогда, когда длина волны де Бройля не мала по сравнению с размерами объектов, с которыми происходит взаимодействие. В процессах взаимодействия атомов с электронами и другими мельчайшими частицами, для которых длина волны де Бройля порядка атомных размеров, волновые свойства частиц играют с у щ е с т в е н н у ю и даже о п р е д е л я ю щ у ю роль. Тем более это относится к процессам, связанным с поведением электронов в н у т р и атомов или молекул.