
Физика. Теоретические курсы / Ландсберг Г.С. Элементарный учебник физики / Ландсберг Г.С. Элементарный учебник физики. Том 3
.pdfГл. X. Применение отражения и преломления света |
241 |
Пусть C1 и C2 — центры сферических преломляющих поверхностей линзы, а R1 и R2 — соответственно радиусы этих поверхностей. Радиус C1M перпендикулярен к касательной плоскости AB, а радиус C2M — к касательной плоскости AB . По известной теореме геометрии угол между этими перпендикулярами, который мы обозначим ψ, равен углу θ между плоскостями:
ψ = θ. |
(88.3) |
С другой стороны, угол ψ, как внешний угол в треугольнике C1N C2, равен сумме углов γ1 и γ2, образуемых радиусами R1
и R2 |
с осью: |
(88.4) |
|
ψ = γ1 + γ2. |
|
Таким образом, с помощью формул (88.2)–(88.4) находим |
|
|
|
ϕ = (n − 1)(γ1 + γ2). |
(88.5) |
Мы предположили, что h м а л а по сравнению с радиусами сферических поверхностей R1 и R2 и с расстоянием f точки F от оптического центра линзы. Поэтому углы γ1, γ2 и ϕ также малы, и мы можем заменить синусы этих углов самими углами. Далее, благодаря тому, что линза тонкая, мы можем пренебречь ее толщиной, считая C1O = R1; C2O = R2, а также пренебречь разницей в высоте точек M и M , считая, что они расположены на одной и той же высоте h над осью. Таким образом, мы можем п р и б л и ж е н н о считать, что
|
|
h |
|
|
|
|
|
|
h |
|
|
|
|
|
h |
|
|||||||
γ1 ≈ sin γ1 = |
|
, |
|
|
γ2 ≈ sin γ2 = |
|
|
|
, |
|
ϕ ≈ sin ϕ = |
|
. |
(88.6) |
|||||||||
R1 |
R2 |
f |
|||||||||||||||||||||
Подставляя эти равенства в формулу (88.5), найдем |
|
|
|
||||||||||||||||||||
|
|
|
|
|
h |
= (n − 1) |
|
|
|
h |
+ |
|
h |
, |
|
|
(88.7) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
f |
R1 |
|
R2 |
|
|
||||||||||||||
или, сокращая на h, |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
||||||
|
1 |
= (n − 1) |
|
|
1 |
|
+ |
1 |
|
|
|
(88.8) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
f |
R1 |
|
R2 |
|
|
|||||||||||||
отсюда |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
f = |
|
|
|
|
|
|
|
|
|
. |
|
|
(88.9) |
|||||
|
|
|
|
|
(n − 1) R1 |
+ |
R2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
||
Весьма |
существенно, что |
h |
|
н е |
|
в х о д и т в |
о к о н ч а- |
||||||||||||||||
т е л ь н ы й |
р е з у л ь т а т. Это означает, что л ю б о й |
луч, па- |
|||||||||||||||||||||
раллельный главной оптической оси линзы, встречающий линзу на любом, но д о с т а т о ч н о м а л о м по сравнению с R1 и R2
242 |
Гл. X. Применение отражения и преломления света |
расстоянии h от оси, пройдет после преломления в линзе ч е р е з |
|
о д н у |
и т у ж е т о ч к у F , лежащую на расстоянии f от |
оптического центра линзы. |
|
Таким образом, д о к а з а н о, ч т о л и н з а и м е е т г л а в- |
|
н ы й |
ф о к у с, и формула (88.9) показывает, как фокусное рас- |
стояние зависит от показателя преломления вещества, из кото- |
|
рого сделана линза, и от радиусов кривизны ее преломляющих |
|
поверхностей. |
|
Мы предполагали, что параллельный пучок лучей падает на |
|
линзу слева направо. Существо дела не изменится, конечно, если |
|
на линзу направить такой же пучок лучей, идущих в обратном |
|
|
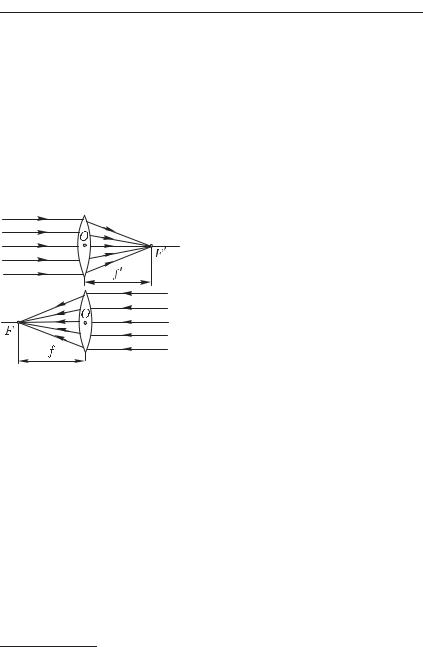
направлении, т. е. справа налево. |
|
Этот пучок лучей, параллельных |
|
главной оси, соберется снова в од- |
|
ной точке F — втором фокусе лин- |
|
|
зы (рис. 196) на расстоянии f от |
|
|
ее оптического центра. На осно- |
|
|
вании формулы (88.9) заключаем, |
|
|
что f = f , т. е. оба фокуса лежат |
|
|
симметрично по обе стороны лин- |
|
|
зы 1). |
называется обычно |
Рис. 196. Фокусы линзы |
Фокус F |
|
передним фокусом, фокус F — |
||
|
задним фокусом; соответственно |
|
этому расстояние f называется передним фокусным расстояни- |
||
ем, расстояние f — задним фокусным расстоянием. |
||
Если в фокусе линзы поместить т о ч е ч н ы й источник све- |
||
та, то каждый из лучей, выйдя из этой точки и преломившись |
||
в линзе, пойдет далее параллельно главной оптической оси лин- |
||
зы, в согласии с законом обратимости световых лучей (см. § 82). |
||
Таким образом, из линзы выйдет в этом случае пучок лучей, |
||
п а р а л л е л ь н ы х главной оси. |
|
|
При практическом применении полученных нами соотноше- |
||
ний необходимо всегда помнить о сделанных при выводе их |
||
упрощающих предположениях. Мы считали, что параллельные |
||
лучи падают на линзу на очень малом расстоянии от оси. Это |
||
условие не выполняется вполне строго. Поэтому после преломле- |
||
ния в линзе точки пересечения лучей не будут строго совпадать |
||
1) Этот вывод связан с тем обстоятельством, что мы с самого начала полагаем, что по обе стороны линзы находится одна и та же среда (воздух). Если бы это было не так, то нарушилась бы и симметрия в расположении фокусов F и F .

Гл. X. Применение отражения и преломления света |
243 |
между собой, а займут некоторый конечный объем. Если мы поставим в этом месте экран, то получим на нем не геометрическую точку, а всегда более или менее расплывчатое светлое пятнышко.
Другое обстоятельство, которое нужно помнить, состоит в том, что мы не можем осуществить строго точечный источник света. Поэтому, поместив в фокусе линзы источник хотя бы очень малых, но всегда к о н е ч н ы х р а з м е р о в, мы не получим с помощью линзы с т р о г о п а р а л л е л ь н ы й пучок лучей.
В§ 70 было указано, что строго параллельный пучок лучей не имеет физического смысла. Сделанное замечание показывает, что рассмотренные свойства линзы находятся в согласии с этим общим физическим положением.
Вкаждом отдельном случае применения линзы к определенному источнику света для получения параллельного пучка лучей или, наоборот, при применении линзы для ф о к у с и р о в-
ки параллельного пучка надо специально проверять степень отступления от тех упрощающих условий, при которых выведены формулы. Но с у щ е с т в е н н ы е черты явления преломления световых лучей в линзе эти формулы передают правильно, а об отступлениях от них речь будет идти позже.
§ 89. Изображение в линзе точек, лежащих на главной оптической оси. Формула линзы. Пусть точечный источник
света находится в точке S на главной оптической оси линзы, на расстоянии a от ее оптического центра O (рис. 197). Рассмотрим, как будет преломляться в линзе у з к и й п у ч о к лучей, примыкающий к прямой SO, являющейся осью этого пучка 1).
Пусть один из лучей (SM ) светового пучка падает на первую преломляющую поверхность линзы в точке M , находящейся на высоте h над осью. То обстоятельство, что мы ограничиваемся узким пучком лучей, означает, что h мало по сравнению с расстоянием a от источника до линзы. С другой стороны, так же как и в § 88, будем считать, что h мало по сравнению с f , а следовательно, и по сравнению с радиусами R1 и R2 ограничивающих линзу поверхностей. Угол, образуемый лучом SM с осью, обозначим γ. Так как h мало, то и угол γ мал. Преломленный луч пойдет по направлению M M и, преломившись снова на второй ограничивающей линзу поверхности, выйдет из линзы по направлению M S , составляющему с осью угол γ .
1) Такие пучки обычно называют параксиальными (приосевыми).

244 |
Гл. X. Применение отражения и преломления света |
Обозначим через a расстояние от оптического центра линзы до точки S , в которой преломленный луч пересекает главную ось.
Как и в предыдущем параграфе, проведем через точки M и M плоскости, касательные к преломляющим поверхностям линзы. Эти плоскости образуют тонкую призму BAB с преломляющим углом θ. Вместо того чтобы рассматривать преломление луча SM M S в линзе, будем рассматривать преломление того же луча в тонкой призме BAB .
Выбранный нами луч после преломления отклонится от первоначального направления на угол α, который по формуле тонкой призмы равен
α = (n − 1)θ, |
(89.1) |
где n — показатель преломления вещества, из которого сделана линза.
Рис. 197. Преломление в линзе луча SM , выходящего из точки S на оси. Угол BAB и толщина линзы сильно преувеличены
Рассмотрим также луч P M , идущий параллельно главной оси и падающий на линзу в точке M . Преломление такого луча уже рассмотрено в § 88 (условие малости h здесь соблюдено). Мы знаем, что после преломления в линзе этот луч выйдет из точки M под углом ϕ к оси и пройдет через главный фокус F на расстоянии f от оптического центра. Точки M и M очень близки друг к другу, так что призмы, образованные касательными в точке M и точках M или M , практически не различаются и имеют один и тот же преломляющий угол θ. Угол α , на который отклонится этот луч от первоначального направления после преломления в тонкой призме, равен опять

Гл. X. Применение отражения и преломления света |
245 |
(n − 1)θ, т. е. равен углу α. С другой стороны, этот угол α равен, очевидно, углу ϕ (рис. 197). Таким образом, получаем
α = α = ϕ. |
(89.2) |
Но угол α как внешний угол в треугольнике SN S равен сумме |
|
γ + γ . Итак, имеем |
|
γ + γ = ϕ. |
(89.3) |
Лучи SM , M S и M F идут под небольшими углами к оси, т. е. углы γ, γ и ϕ малы. Заменяя, как и в предыдущем параграфе, синусы малых углов самими углами и пренебрегая толщиной линзы и разницей в высоте точек M , M и M над осью, можно приближенно написать:
γ ≈ sin γ = ha , γ ≈ sin γ = ah , ϕ ≈ sin ϕ = fh . (89.4)
Подставляя эти приближенные равенства в формулу (89.3), находим
h |
+ |
|
h |
= |
|
h |
, |
(89.5) |
|||
|
a |
|
|
|
|
||||||
|
|
|
a |
|
|
f |
|
||||
или, сокращая на общий множитель h, |
|
||||||||||
1 |
+ |
1 |
|
= |
1 |
. |
(89.6) |
||||
|
a |
|
|
||||||||
|
|
a |
|
f |
|
||||||
В правой части полученного выражения стоит величина 1/f , которая, как мы видели в предыдущем параграфе, зависит т о л ь- к о о т с в о й с т в л и н з ы — от показателя преломления вещества, из которого сделана линза, и от радиусов кривизны ее преломляющих поверхностей.
То обстоятельство, что в формулу (89.6) не входит величина h, позволяет сделать очень в а ж н ы е в ы в о д ы, а именно, что не только луч SM , но и всякий другой луч, выходящий из точки S, пройдет после преломления в линзе через одну и ту же точку S , хотя каждый из этих лучей падает на линзу на р а з н о й высоте над осью. Единственное, но весьма существенное огра-
ничение, которое мы накладываем на рассматриваемые |
л у ч и, |
состоит в том, что все о н и с о с т а в л я ю т с о с ь ю |
л и н з ы |
м а л ы е у г л ы. |
|
Таким образом, все лучи узкого пучка, выходящие из точки S, соберутся после преломления в линзе снова в одной точке S , являющейся изображением точки S. Мы доказали, следовательно, что образующееся в тонкой линзе изображение точечного источника, лежащего на главной оси линзы, полученное с помощью достаточно узкого пучка лучей, является точкой.

246 Гл. X. Применение отражения и преломления света
Изображения, при получении которых выполнено условие передачи к а ж д о й т о ч к и объекта о д н о й т о ч к о й изображения, носят название стигматических. Изображения, у ко-
торых это условие не соблюдено, носят название астигматических 1).
Отметим, что в силу закона обратимости световых лучей (§ 82) положения источника света S и его изображения S о б- р а т и м ы, т. е., поместив источник в S , мы получим его изображение в точке S. Точки S и S называются сопряженными.
В геометрической оптике особое значение имеет задача получения стигматических изображений. Степень стигматичности изображений определяет качество служащих для их получения оптических систем. Нарушение оптической системой стигматичности падающих на нее световых пучков ведет к расплывчатости изображения. В дальнейшем при изучении простейших оптических систем мы будем уделять большое внимание вопросу о стигматичности даваемых ими изображений.
Полученная нами формула (89.6) связывает между собой расстояния от оптического центра трех точек, находящихся на главной оси линзы: источника S, его изображения S и фокуса F . Это — основная формула тонкой линзы.
§ 90. Применения формулы тонкой линзы. Действительные и мнимые изображения. Предположим, что светящаяся точка
S, лежащая на главной оси линзы, удаляется от линзы на очень большое расстояние. В этом случае лучи, падающие на линзу, будут стремиться стать параллельными ее главной оси. Мы видели в § 88, что после преломления в линзе эти лучи соберутся в фокусе F линзы. В формуле (89.6) при удалении источника на очень большое расстояние величина 1/a стремится к нулю,
и мы получаем
a = f ,
т. е. можно сказать, что фокус F есть изображение «бесконечно удаленной» точки.
Примером практически бесконечно удаленного источника может служить любое небесное тело. Следовательно, изображения звезд, Солнца и т. д. будут находиться в фокусе линзы. Достаточно далекие от линзы земные источники света также дают изображение в ее фокусе.
1) С т и г м а значит по-гречески точка, стигматический — точечный, частица «а» впереди слова — знак отрицания. Астигматический значит неточечный.

Гл. X. Применение отражения и преломления света |
247 |
Предположим теперь, что изображение некоторой точки удалено на очень большое расстояние, т. е. из линзы выходит пучок световых лучей, параллельных главной оси. В этом случае, как мы видели в § 88, источник должен находиться в переднем фокусе линзы F (рис. 196). Этот вывод следует и из формулы (89.6). Действительно, полагая, что изображение находится в бесконечности, получаем 1/a = 0; при этом расстояние источника от линзы равно фокусному расстоянию: a = f = f .
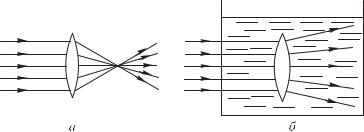
Различные линзы отличаются одна от другой расположением центров образующих их сферических поверхностей, их радиусами и показателями преломления вещества, из которого сделаны линзы. На рис. 198 представлены шесть основных типов линз.
Рис. 198. Различные типы линз. Если материал линз преломляет сильнее, чем окружающая среда, то типы а, б, в — собирающие; типы г, д, е — рассеивающие
Если параллельные лучи после преломления в линзе с х о- д я т с я, действительно пересекаясь в некоторой точке, лежащей по другую сторону линзы, то линза называется собирающей или положительной (рис. 199, а). Если же параллельные лучи
Рис. 199. Действительный фокус собирающей линзы (а) и мнимый фокус рассеивающей линзы (б)
после преломления в линзе становятся р а с х о д я щ и м и с я (рис. 199, б), то линза называется рассеивающей или отрицательной. В случае рассеивающей линзы в фокусе пересекаются не преломленные лучи, а их воображаемые продолжения; при этом фокус лежит с той же стороны от линзы, с которой падает на линзу параллельный пучок лучей. Фокусы в этом случае называются мнимыми (рис. 199, б).
Обычно материал линзы преломляет сильнее, чем окружающая среда (например, стеклянная линза в воздухе). Тогда собирающими линзами являются линзы, утолщающиеся от краев к середине, — двояковыпуклая и плосковыпуклая линзы и положительный мениск (вогнуто-выпуклая линза; рис. 198, а–в). Рассеивающими линзами являются линзы, становящиеся тоньше
248 |
Гл. X. Применение отражения и преломления света |
к середине: двояковогнутая, плоско-вогнутая линзы и отрицательный мениск (выпукло-вогнутая линза; 198, г–д). Если материал линзы преломляет слабее, чем окружающая среда, т. е. относительный показатель преломления n < 1, то, наоборот, линзы а, б, в (рис. 198) будут рассеивающими, а линзы г, д,
Рис. 200. Двояковыпуклые линзы: а) стеклянная в воздухе — собирающая; б) воздушная в воде — рассеивающая
е — собирающими. Такие линзы можно получить, например, образовав в воде двумя часовыми стеклами, склеенными воском, воздушную полость соответствующей формы (рис. 200).
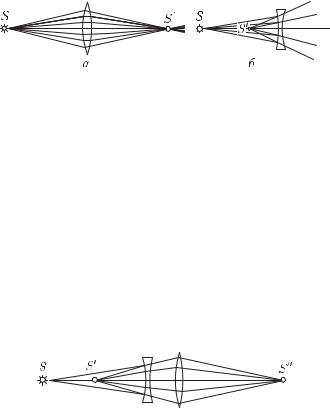
Перейдем к рассмотрению светящихся точек, находящихся на конечном расстоянии от линзы. Будем всегда считать источники расположенными с л е в а о т л и н з ы. Что касается изображений, то в зависимости от вида линзы и положения источника относительно нее изображение S может находиться как справа, так и слева от линзы. Если изображение лежит справа от линзы, то это означает, что оно образовано сходящимся пучком лучей (рис. 201, а), т. е. лучей, которые действительно проходят через точку S . Изображение в этом случае называется действительным. Оно может быть получено на экране, фотопластинке и т. п. Восстановив ход лучей, приведших к образованию и з о б р а ж е- н и я, мы можем всегда найти местоположение и с т о ч н и к а, хотя практически это обычно связано с некоторыми трудностями.
Предположим теперь, что изображение лежит слева от линзы, т. е. с той же стороны от нее, как и источник. Это означает, что пучок лучей, расходящихся от источника, после преломления в линзе становится еще более расходящимся, и в точке S пересекаются лишь воображаемые п р о д о л ж е н и я преломленных лучей (рис. 201, б). Изображение в этом случае называется
мнимым.
Укоренившийся в оптике термин «мнимое изображение» может привести к некоторым недоразумениям. В действительности
Гл. X. Применение отражения и преломления света |
249 |
ничего «мнимого» в этом случае, конечно, нет. Особенностью мнимых изображений является то, что их нельзя получить непосредственно на экране, фотопластинке и т. п. Например, если поместить в точке S (рис. 201, б) очень маленький экран, не мешающий попаданию основной части лучей на линзу, то мы
Рис. 201. Источник и действительное изображение лежат с разных сторон от линзы (а); мнимое изображение находится с той же стороны от линзы, что и источник (б)
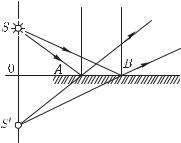
не получим на нем светящейся точки. Однако р а с х о д я щ и й- с я п у ч о к л у ч е й, воображаемые продолжения которых пересекаются в мнимом изображении, сам по себе не имеет ничего «мнимого». Этот пучок можно превратить в сходящийся пучок, если на пути его поставить надлежащим образом выбранную собирающую линзу. Тогда на экране или фотопластинке мы будем иметь реальное изображение S светящейся точки S (рис. 202), которое в то же время можно рассматривать как изображение «мнимой точки» S .
Роль подобной собирающей линзы выполняет также глаз человека; на светочувствительной оболочке глаза — сетчатке — собираются расходящиеся от источников света лучи. Пучок расходящихся лучей, исходят ли они от реального точечного
Рис. 202. Превращение расходящегося пучка лучей в сходящийся с помощью вспомогательной собирающей линзы (например, глаза)
источника S или от его мнимого изображения S , может быть собран оптической системой глаза в одну точку на сетчатке. В повседневной жизни наблюдатель приобретает привычку автоматически восстанавливать ход лучей, давших изображение на сетчатке, и определять местоположение источника. Когда в глаз попадает расходящийся пучок лучей (с вершиной в S ), изображенный на рис. 202, то, «восстанавливая» место, откуда вышли эти лучи, мы в и д и м в точке S источник, хотя в действи-
250 |
Гл. X. Применение отражения и преломления света |
тельности в данной точке источника нет. Этот-то воображаемый источник мы и называем «мнимым» изображением точки S.
Пользуясь формулой (89.6), нетрудно проследить, как меняется положение изображения по мере перемещения источника вдоль главной оптической оси (см. упражнения 31, 32 в конце этой главы).
§ 91. Изображение точечного источника и протяженного объекта в плоском зеркале. Изображение точечного источника в сферическом зеркале. Мы переходим теперь к задаче
нахождения изображений при отражении света от различного типа зеркал. Законы образования изображений светящихся точек при отражении в зеркале и при преломлении в линзе во многом аналогичны.
Эта аналогия, конечно, не случайна; она обусловлена тем, что формально, как мы видели в гл. IX, закон отражения является частным случаем закона преломления (при n = −1).
Наиболее просто решается поставленная нами задача для отражения световых лучей от п л о с к о г о з е р к а л а. Вместе с тем отражение света от плоского зеркала представляет собой наиболее простой и общеизвестный случай образования мнимых изображений, рассмотренных в предыдущем параграфе.
Пусть пучок лучей от точечного источника S (рис. 203) падает на плоское зеркало (металлическое зеркало, поверхность воды и т. д.). Проследим, что про- 
 изойдет с этим конусом лучей,
изойдет с этим конусом лучей,
имеющим вершину в точке S.
Возьмем два п р о и з в о л ь н ы х
луча SA и SB. Каждый из них
отразится по закону отражения, и угол каждого из них с нормалью останется после отражения неиз-
менным. Следовательно, останется неизменным и угол м е ж д у лучами после отражения.
Этот угол между отраженными лучами можно изобразить на рисунке, продолжив отраженные лу-
чи назад, за плоскость зеркала, что показано на чертеже штриховыми линиями. Точка пересечения S продолжения лучей за зеркалом будет лежать на т о й ж е н о р м а л и к зеркалу, что и точка S, и на т о м ж е р а с с т о я н и и от плоскости зеркала,
