Оценка погрешностей прямых и косвенных измерений. Содержание лабораторной работы

Метрология — учение о мерах. Это наука об измерениях, приводимых к эталонам. Каждое измерение может осуществляться лишь с помощью технических средств, имеющих необходимую точность. Эта точность может быть обеспечена путем их поверки, то есть сравнения с более точными измерительными средствами с целью определения погрешностей.

Цель любого исследования — установление связи между различными явлениями и параметрами. Количественная зависимость между исследуемыми величинами получается в результате измерений.

Измерение — это нахождение значения физической величины опытным путем, техническими средствами. Выбор единиц диктуется практическими соображениями, однако основой является Международная система единиц (СИ), поэтому окончательный результат измерений следует по возможности выражать в единицах СИ.

Физическая величина — это количественное значение параметров оцениваемых физико-химических процессов, происходящих в любых реальных объектах. Это понятие может быть обобщенным (например, масса, длина, скорость и т.п.), и может быть конкретным (частота пульса, скорость кровотока, длина руки и т.д.).

Технические средства, или просто средства измерения, — это в общем измерительные приборы, в которых измеренная информация представляется в доступной для восприятия форме (например, в виде цифр).

Измерения по способу получения результата бывают прямые и косвенные.

Прямые измерения заключаются в том, что искомое значение величины находят из опытных данных путем экспериментального сравнения. Например, температуру тела измеряют термометром, длину — линейкой.

Уравнение прямого измерения:

,

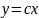где с — цена деления; х — число делений.

Косвенные измерения заключаются в том, что искомое значение величины находят на основании известной зависимости (формулы) между этой величиной и величинами, найденными прямыми измерениями. Например, объем шара: 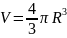, сопротивление: .

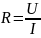Уравнение косвенного измерения:

,

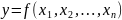где 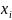 — результат прямого измерения.

Значение физической величины, полученное при измерении, отличается от истинного. Точность измерений характеризуется погрешностью — отклонением результата измерений от истинного значения искомой величины. Чем меньше погрешность, тем выше точность.

Погрешность измерения 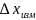 — это отклонение результата измерения х от истинного (действительного) х_и значения измеряемой величины:

.

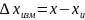На точность измерения влияет большое количество факторов, поэтому оценка погрешности очень важна для обеспечения единства измерений. Классификация погрешностей измерений очень обширна.

Для практических целей достаточно рассмотреть систематические и случайные составляющие общей погрешности, выраженные в абсолютных и относительных единицах при прямых и косвенных измерениях.

Абсолютная погрешность измерения ∆ — это разность между результатом измерения х и фактическим значением х_ф измеряемой величины:

.

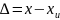
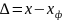Она выражается в тех же единицах, что и сама измеряемая величина.

Относительная погрешность измерения δ — это отношение абсолютной погрешности к самой измеряемой величине х или к ее фактическому значению х_ф. Выражается в процентах:

.

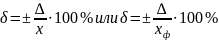Погрешности прямых измерений

Различают четыре типа погрешностей измерений:

1. грубые (промахи);

2. систематические;

3. инструментальные;

4. случайные.

Грубыми погрешностями, или промахами, называют погрешности измерения, которые значительно отличаются от ожидаемых при данных условиях. Такие погрешности возникают по вине экспериментатора или под влиянием внешних причин, не имеющих отношения к эксперименту. Грубые ошибки могут быть установлены интуитивно, т.к. результаты измерения в этих случаях резко отличаются от остальных. Иногда для их исключения проводятся измерения в других условиях или в другое время. В любом случае грубые промахи должны быть исключены.

Систематическая погрешность остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины одним и тем же прибором. Такие погрешности определяются неточностью методики эксперимента, неисправностью прибора или отсутствием учета некоторых факторов, влияющих на точность измерения. Погрешности метода могут заключаться в неточности формул, по которым рассчитываются физические величины. Такие погрешности можно уменьшить введением поправочных коэффициентов к расчетным формулам.

Инструментальные погрешности, или погрешности измерительных приборов, возникают из-за неисправности или недостаточной точности средства измерения. Для их устранения необходимо использовать измерительные средства, прошедшие метрологическую поверку и имеющие соответствующий класс точности. Например, если цена деления амперметра 1 мА, то абсолютная ошибка прибора Δ = 0,5 мА и измерять изменения силы тока в пределах 0,5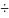 0,05 мА таким прибором нельзя.

Случайные погрешности возникают под воздействием факторов, влияние которых учесть нельзя. Под воздействием неучтенных факторов результаты измерения могут отличаться. К числу таких факторов могут относиться как внешние воздействия (температура, давления, электрические и магнитные поля, звуковые явления и т.п.), так и внутренние, обусловленные состоянием организма человека. Однако, при повторных измерениях, проводимых в одинаковых условиях, возможно выявить характерную закономерность результатов. Для этого применяются методы теории вероятностей и математической статистики, позволяющие установить наиболее вероятное значение измеряемой величины и оценить погрешность измерения.

При прямых измерениях существуют два способа оценки случайных погрешностей:

• упрощенное определение — это очень упрощенный метод обработки результатов малого числа измерений;

• оценка измеряемой величины при помощи доверительного интервала.

1. Рассмотрим упрощенное определение случайных погрешностей при прямых измерениях.

Прямые измерения — это измерения, непосредственно определяющие физическую величину при помощи прибора.

Пусть проведено n измерений величины х и получено n значений: x₁, x₂, …, x_n.

1) Вычислить среднюю арифметическую .

.

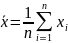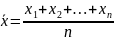2) Вычислить абсолютную погрешности результатов отдельных наблюдений.

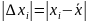, где i = 1, 2, …, n.

, , … , .

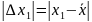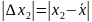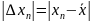3) Найти среднюю абсолютную погрешности опыта.

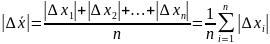
4) Вычислить относительную погрешность δ эксперимента, так как средняя абсолютная погрешность не характеризует точности измерения.

.

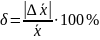Относительная погрешность показывает, какая часть абсолютной погрешности приходится на каждую единицу измеряемой величины. Это очень упрощенный метод обработки результатов малого числа измерений, который в научных исследованиях не применяется.

2. Рассмотрим оценку измеряемой величины при помощи доверительного интервала при прямых измерениях. Она проводится следующим образом:

Случайные погрешности нельзя исключить полностью, но их влияние может быть уменьшено путем обработки результатов измерений. Для этого должны быть известны вероятностные и статистические характеристики: закон распределения, математическое ожидание, среднее квадратическое отклонение, доверительный интервал и доверительная вероятность.

Доверительный интервал — это интервал, в котором с той или иной заранее заданной вероятностью находится искомая величина.

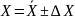
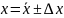, где 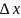 — случайная погрешность. .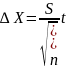

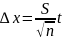Алгоритм оценки доверительного интервала

Пусть проделано n измерений некоторой величины X. В результате получен ряд значений этой величины: x₁, x₂, …, x_n.

1. Вычислить среднее арифметическое значение измеряемой величины:

.

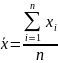2. Вычислить среднюю квадратическую погрешность (стандарт) по формуле: 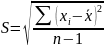до одной значащей цифры.

3. Задать уровень доверительной вероятности. Обычно Р ≥ 0,95.

4. По табл. 1.1 найти t_n,p — нормированный показатель распределения Стьюдента: t_n,p.

Таблица 1.1

Значения нормированного показателя распределения Стьюдента

n — объем выборки	Р ≥ 0,9	Р ≥ 0,95	Р ≥ 0,99
2	4	13	64
3	3	4,6	10
4	2,3	3,2	5,8
5	2,1	2,8	4,6
6	2,0	2,6	4,0
8	1,9	2,3	3,5
10	1,8	2,2	3,2
20	1,8	2,1	2,8
30	1,7	2,0	2,7
50	1,6	1,9	2,6

5. Вычислить случайную погрешность .

6. Рассчитать границы доверительного интервала и записать окончательный вариант (P≥0,95).

Погрешность при вычислении округляется до первой значащей цифры.

Например: =6,784 ≈7; =0,784 ≈ 0,8; =0,084 ≈0,08