5 Правило Рунге практической оценки погрешности

Оценки погрешности по формулам ( 4), ( 8) и ( 12) являются априорными. Они зависят от длины элементарного отрезка h, и при достаточно малом h справедливо приближенное равенство:

I – I^h  Ch^k, ( 15)

где I^h приближенное значение интеграла, вычисленное по одной из формул ( 3), ( 5), ( 9), C  0 и k > 0 – величины, не зависящие от h.

Если уменьшить шаг h в два раза, то, в соответствии с ( 15) получим:

I – I^h/2  Ch^k  ( I – I^h). ( 16)

Непосредственное использование оценок погрешности ( 4), ( 8) и ( 12) неудобно, так как при этом требуется вычисление производных функции f (x). В вычислительной практике используются другие оценки.

Вычтем из равенства ( 15) равенство ( 16):

I^h/2 – I^h  Ch^k(2^k – 1). ( 17)

Учитывая приближенное равенство ( 16), получим следующее приближенное равенство:

I – I^h/2 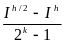 . ( 18)

Приближенное равенство ( 18) дает апостериорную оценку погрешности. Вычисление этой оценки называется правилом Рунге. Правило Рунге – это эмпирический способ оценки погрешности, основанный на сравнении результатов вычислений , проводимых с разными шагами h.

Для формул прямоугольников и трапеций k = 2, а для формулы Симпсона k = 4. Поэтому для этих формул приближенное равенство ( 18) принимает вид:

I – I_пр  , ( 19)

I – I_тр  , ( 20)

I – I_С  . ( 21)

Используя правило Рунге, можно построить процедуру приближенного вычисления интеграла с заданной точностью . Нужно, начав вычисления с некоторого значения шага h, последовательно уменьшать это значения в два раза, каждый раз вычисляя приближенное значение I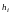 . Вычисления прекращаются тогда, когда результаты двух последующих вычислений будут различаться меньше, чем на .

Пример 4.

Найдем значение интеграла с точностью  = 10^-4, используя формулу трапеций и применяя вышеизложенную процедуру дробления шага. В примере 2 было получено значение I при h₁ = 0.1, I^h =0.74621079. Уменьшим шаг вдвое: h₂ = 0.05 и вычислим I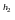 = 0.74667084, ₂ = ( I - I ) = (0.74667084 – 0.74621079)  1.510^-4. Так как |₂| > , то снова дробим шаг: h₃ = 0.025, вычисляем I = 0.74678581, ₂ = ( I - I ) = (0.74678581 – 0.74667084)  410^- Поскольку |₃| < , требуемая точность достигнута и I  0.7468  0.0001.