
lec13
.pdfТеорема об эквивалентности автоматов Мили и Мура.
Теорема 13.1. автомата Мили существует, покрывающий его автомат Мура. Т.е. существует автомат Мура, который может производить все автоматные отображения, которые производит исходный автомат Мили.
Доказательство: Допустим у исходного автомата множество Q={q1,…,qn} X={x1,…,xm}. Надо построить автомат Мура, который делает все тоже самое, что и исходный. Построим автомат Мура. Mʹ = {X, Qʹ, Y, φʹ, ψʹ}, у которого
Qʹ = {q10…qr0, q11…qr1, …, q1n...qnr}
Функции определим следующим образом
φʹʹ(qi0) = - φʹ(qij) = F(xj,qi)
ψʹ(xk,qi0) = qik
ψʹ(xk,qij) = qlk,
где l определяется из следующего условия: ql = ψ(xj,qi).
21
Продолжение доказательства теоремы 13.1.
Доказательство (продолжение):
Если исходный автомат находится в состоянии qi и на вход подается символ |
|||||||||||||||||||||||||||
xj, то исходный автомат переходит в состояние ql = ψ(xj,qi). Построенный |
|
||||||||||||||||||||||||||
автомат Мура Мʹ покрывает исходный автомат М. Для всякого состояния qi |
|||||||||||||||||||||||||||
автомата М, покрывающим для него состоянием является qi0 |
Q |
|
|||||||||||||||||||||||||
Пусть α = xi1, xi2…xis X* любое входное слово, тогда φ(qi,α) = -, yk1, yk2…yks-1 – |
|||||||||||||||||||||||||||
выходное слово. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим соответствующее выходное слово автомата Мʹ, если он |
|
||||||||||||||||||||||||||
находится в каждый момент времени в состоянии qi0 |
и покажем, что эти два |
||||||||||||||||||||||||||
слова совпадают, если прочерк не учитывать. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
+1 |
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
Q |
|
|
|
… |
|
|
|
Q |
|
|
Q |
|
||||||||
M: Q |
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
+1 |
|
||||||||
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1 |
|
|
|
|||
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
+1 |
|
|
|
|||
1 |
Q |
|
|
Q |
|
|
… |
|
|
|
|
Q |
|
|
|
Q |
|
||||||||||
Mʹ: Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
0 − |
|
1 |
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
−1 |
|
|
|
+1 |
|
||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
−1 |
|
|
|
|
|
22 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
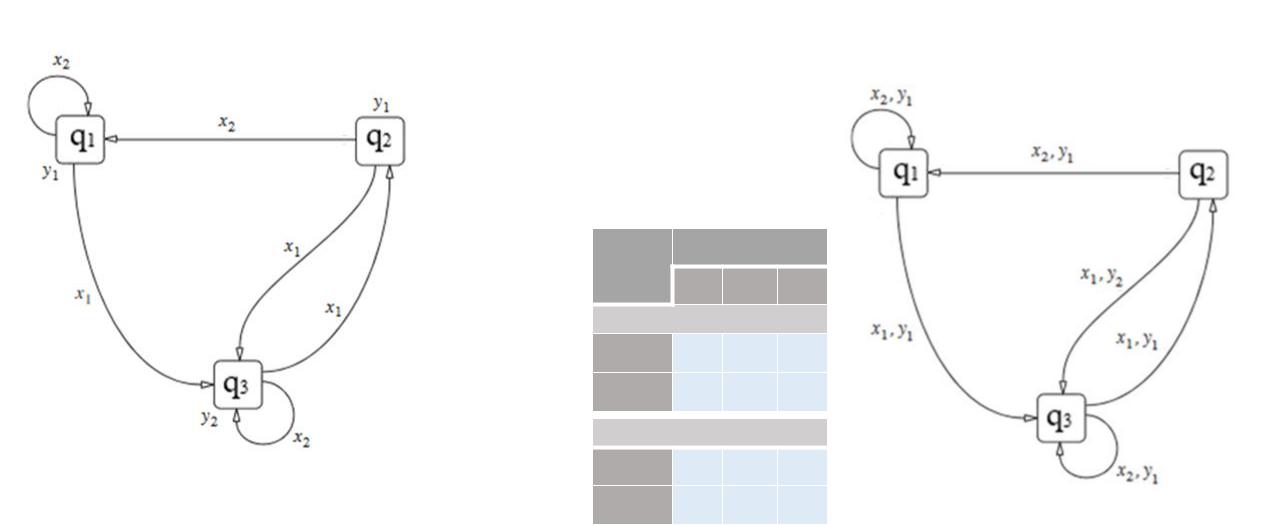
Пример 13.2. Работа эквивалентных автоматов Мили и Мура. |
|
|||||||||
а) простейший случай: для qj характерно одно yi (в т.ч. RS-, JK-триггеры). |
|
|||||||||
Задание автомата Мура. |
|
|
|
|
|
|
|
|
|
|
X |
|
Q |
|
|
|
|
|
Задание эквивалентного |
||
|
|
y1 |
y1 |
|
|
y3 |
|
|
автомата Мили. |
|
|
|
|
|
|
|
|
|
|
||
|
|
q1 |
q2 |
|
q3 |
|
|
|
|
|
|
x1 |
q3 |
q3 |
|
q2 |
|
|
|
|
|
|
x2 |
q1 |
q1 |
|
q3 |
|
|
|
|
|
|
|
|
|
X |
|
|
Q |
|
|
|
|
|
|
|
|
|
|
q1 |
q2 |
q3 |
|
|
|
|
|
|
|
Переходы |
|
|
||
|
|
|
|
x1 |
|
q3 |
q3 |
q2 |
|
|
|
|
|
|
x2 |
|
q1 |
q1 |
q3 |
|
|
|
|
|
|
|
|
выходы |
|
|
||
|
|
|
|
x1 |
|
y1 |
y1 |
y2 |
|
|
|
|
|
|
x2 |
|
y1 |
y1 |
y2 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
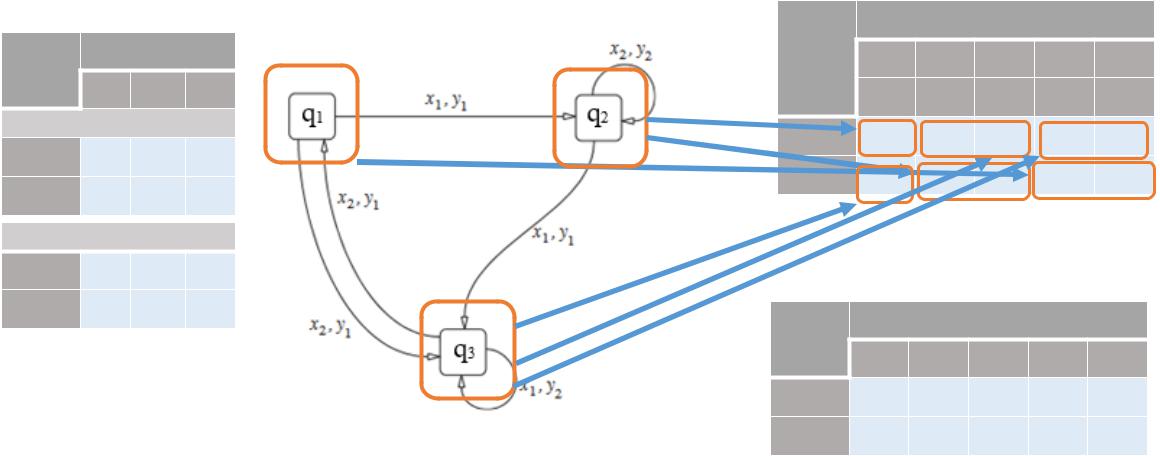
Пример 13.2. Работа эквивалентных автоматов Мили и Мура.
б) для некоторых qj характерно несколько yi. Автомат Мили (пример 13.1).
X |
|
Q |
|
|
q1 |
q2 |
q3 |
|
переходы |
|
|
x1 |
q2 |
q3 |
q3 |
x2 |
q3 |
q2 |
q1 |
|
выходы |
|
|
x1 |
y1 |
y1 |
y2 |
x2 |
y1 |
y2 |
y1 |
Автомат Мура выдает те же самые выходные символы, что и
Автомат Мили с задержкой один такт.
Задание эквивалентного автомата Мура
X |
|
|
QY |
|
|
|
y1 |
y1 |
y2 |
y1 |
y2 |
|
q1 |
q2 |
q2 |
q3 |
q3 |
x1 |
q21 |
q31 |
q31 |
q32 |
q32 |
x2 |
q31 |
q22 |
q22 |
q11 |
q11 |
X |
|
|
Q |
|
|
|
q11 |
q21 |
q22 |
q31 |
q32 |
x1 |
q21 |
q31 |
q31 |
q32 |
q32 |
x2 |
q31 |
q22 |
q22 |
q11 |
q11 |
24
