35.Дифференциальная функция распределения вероятности f(X) всегда

1. -1 <f(x) < 1 2. 0 f(x)  1 3. f(x)  0 4. -<f(x) > +

36. СВОЙСТВА ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ f(x) 1. Используется для дискретных случайных величин 2. Используется для непрерывных случайных величин 3. Площадь под графиком равна 1 4. f(x) ≥0

37. ДИСПЕРСИЯ D(х)– ЭТО 1. М(х-М(х))² 3. М(х²) – (М(х))² 2. (х_i– М(х))² Р_i4. σ²

38. ДАНЫ ДВА РАСПРЕДЕЛЕНИЯ. ДИСПЕРСИЯ БОЛЬШЕ В СЛУЧАЕ А Б

Х	-1	+1
Р	0,5	0,5

Х	-100	+100
Р	0,5	0,5

1. А 2. Б 3. Одинакова 4. Вопрос смысла не имеет

39. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ ИСПОЛЬЗУЕТСЯ ДЛЯ СЛУЧАЙНЫХ ВЕЛИЧИН

1. Непрерывных 2. Дискретных 3. И для дискретных и для непрерывных 4. Для любых случайных величин

40. ПАРАМЕТРЫ ДЛЯ ГРАФИКОВ НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ

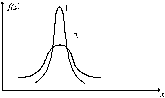
1. 2. 3. 4. 5. 6.

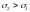
41. ПАРАМЕТРЫ ДЛЯ ГРАФИКОВ НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ

1

4. 5. 6.

.

_2.

_3.

42. ПАРАМЕТРЫ ДЛЯ ГРАФИКОВ НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ

1.

2.

3.

4.

5.

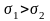
6.

43.ПАРАМЕТРЫ ДЛЯ ГРАФИКОВ НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ

_1. 2. 3. 4. 5. 6.

Д

Инструкция для студентов. При выполнении задания следует написать только пропущенные требуемые слова или формулы, пронумеровав их. Объясните смысл, величин, входящих в формулу.

Или начертите два графика в одних осях координат и отметьте их параметры.

ОПОЛНИТЕ

1. ТЕОРИЯ ВЕРОЯТНОСТИ ИЗУЧАЕТ ЗАКОНОМЕРНОСТИ, ПРИСУЩИЕ ……….... (1) ................(2) СОБЫТИЯМ. 2. СЛУЧАЙНОЕ СОБЫТИЕ - ЭТО СОБЫТИЕ, НАСТУПЛЕНИЕ КОТОРОГО.............(1) …….........(2) ПРЕДВИДЕТЬ. ОБОЗНАЧАЕТСЯ................(3). 3. СТАТИСТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ: ВЕРОЯТНОСТЬЮ СЛУЧАЙНОГО СОБЫТИЯ НАЗЫВАЮТ…. ......(1), К КОТОРОМУ СТРЕМИТСЯ .......(2) ПРИ НЕОГРАНИЧЕННОМ УВЕЛИЧЕНИИ ....... (3)....... (4). ФОРМУЛА:..............(5).

4. СОГЛАСНОКЛАССИЧЕСКОМУ ОПРЕДЕЛЕНИЮ ВЕРОЯТНОСТЬ ОПРЕДЕЛЯЕТСЯ ПО ФОРМУЛЕ …......(1), ГДЕ ..........(2).

5. НЕВОЗМОЖНОЕ СОБЫТИЕ - ЭТО СОБЫТИЕ, КОТОРОЕ ПРИ ДАННЫХ ИСПЫТАНИЯХ..........(1)...........(2). ЕГО ВЕРОЯТНОСТЬ ..........(3).

6. ДОСТОВЕРНОЕ СОБЫТИЕ - ЭТО СОБЫТИЕ, КОТОРОЕ ПРИ ДАННЫХ ИСПЫТАНИЯХ ...........(1)...........(2). ЕГО ВЕРОЯТНОСТЬ ................(3).

7. НЕСОВМЕСТНЫЕ СОБЫТИЯ - ЭТО СОБЫТИЯ , .....(1) …....(2) КОТОРЫХ ...........(3).

8. РАВНОВОЗМОЖНЫЕ СОБЫТИЯ ИМЕЮТ МЕСТО, ЕСЛИ ПРИ ИСПЫТАНИЯХ …........(1) ..........(2), ИЗ-ЗА КОТОРЫХ ОДНО СОБЫТИЕ ПРОИСХОДИЛО ............(3) ДРУГОГО. ИХ ВЕРОЯТНОСТИ ..............(4).

9. ЗАКОН СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ ДЛЯ ДВУХ НЕСОВМЕСТНЫХ СОБЫТИЙ ИМЕЕТ ВИД ................(1), ГДЕ……(2).

10. УСЛОВИЕ НОРМИРОВКИ ДЛЯ ПОЛНОЙ СИСТЕМЫ СЛУЧАЙНЫХ СОБЫТИЙ ……....(1), ГДЕ……(2).

11. ЗАКОН ПРОИЗВЕДЕНИЯ ВЕРОЯТНОСТЕЙ ДЛЯ ДВУХ НЕЗАВИСИМЫХ СОБЫТИЙ ИМЕЕТ ВИД ...........(1); ДЛЯ ДВУХ ЗАВИСИМЫХ СОБЫТИЙ ..............(2), где…..

12. УСЛОВНАЯ ВЕРОЯТНОСТЬ - ЭТО ВЕРОЯТНОСТЬ СОБЫТИЯ В ПРИ УСЛОВИИ, ЧТО СОБЫТИЕ А ...................(1). ОБОЗНАЧАЕТСЯ ...................(2).

13. ПРОТИВОПОЛОЖНЫЕ СОБЫТИЯ - ЭТО СОБЫТИЯ …......(1) .........(2) И ..........(3).

14. ЗАКОН СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ ДЛЯ ДВУХ СОВМЕСТНЫХ СОБЫТИЙ ИМЕЕТ ВИД ................(1), ГДЕ……(2).

15.СЛУЧАЙНОЙ НАЗЫВАЕТСЯ ВЕЛИЧИНА, СПОСОБНАЯ ПРИ ИСПЫТАНИЯХ ПРИНИМАТЬ ........(1) И ТОЛЬКО ………(2)……….(3)ЗНАЧЕНИЕ, ЗАРАНЕЕ ..............(4).

16. ЗАКОН РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ - ЭТО ......... (1) .........(2) СЛУЧАЙНОЙ ВЕЛИЧИНЫ И ИХ ................(3).

17. УСЛОВИЕ НОРМИРОВКИ ДЛЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ ...........(1), ГДЕ….

18. ВЕРОЯТНОСТЬ ТОГО, ЧТО НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА ПРИНИМАЕТ ЗНАЧЕНИЯ В ИНТЕРВАЛЕ 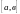ОПРЕДЕЛЯЕТСЯ ПО ФОРМУЛЕ ...........(1), ГДЕ ……......(2).

19. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ДЛЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ ОПРЕДЕЛЯЕТСЯ ПО ФОРМУЛЕ ...........(1), ГДЕ ............ (2), .............(3).

20. ДИСПЕРСИЯ ДЛЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ ОПРЕДЕЛЯЕТСЯ ПО ФОРМУЛЕ .........(1); СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ - ...........(2).

21. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ХАРАКТЕРИЗУЕТ ........(1) ..............(2) СЛУЧАЙНОЙ ВЕЛИЧИНЫ. ДИСПЕРСИЯ ХАРАКТЕРИЗУЕТ ...........................(3)ОТНОСИТЕЛЬНО СРЕДНЕГО.

22. СЛУЧАЙНАЯ ВЕЛИЧИНА РАСПРЕДЕЛЕНА ПО НОРМАЛЬНОМУ ЗАКОНУ, ЕСЛИ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ ВЫРАЖАЕТСЯ ФОРМУЛОЙ ..............(1). ГРАФИК НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ ИМЕЕТ ВИД ..............(2).

23. ГРАФИКИ НОРМАЛЬНЫХ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН, ДЛЯ КОТОРЫХ И , ИМЕЮТ ВИД ..................(1).

24. ГРАФИКИ НОРМАЛЬНЫХ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН, ДЛЯ КОТОРЫХ и , ИМЕЮТ ВИД ..................(1).

25. ГРАФИКИ НОРМАЛЬНЫХ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН, ДЛЯ КОТОРЫХ И , ИМЕЮТ ВИД .....................(1).

У

Инструкция для студентов. Задания состоят в выборе правильных пар из двух множеств. Каждому элементу левого задающего множества L соответствует определенный элемент или два (смотрите эталон ответа) правого множества выбора R.

СТАНОВИТЕ СООТВЕТСТВИЕ

26. СООТВЕТСТВИЕ МЕЖДУ СОБЫТИЯМИ И ЗАКОНАМИ

LR ЗАКОНЫ СОБЫТИЯ

1. Р(А + В) = Р(А)+Р(В) А.Независимые. 2. Р(А +В) = Р(А)+Р(В)-Р(А) Р(В) Б.Зависимые. 3. Р(А • В) = Р(А) Р(В) В. Совместные. 4. Р(А • В) = Р(А) Р(B/A) Г. Несовместные

Эталон: 1 ___, 2___, 3___, ____,4___,____.

27. СООТВЕТСТВИЕ МЕЖДУ НАЗВАНИЕМ И ФОРМУЛОЙ

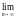
LR НАЗВАНИЕ ФОРМУЛА 1. Статистическое определение вероятности А.Р = 2. Классическое определение вероятности Б. M (x) = 3. Математическое ожидание В. Р = 4.Дисперсия. Г. . Д. D(x)= M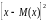

Эталон: 1___, 2__, 3___ , 4 ___ .