
задания 1к 2с / Построение графиков в Python с использованием модуля matplotlib - задания
.docx1.1. Задания: построить график функции одной переменной, x [-5;5]. Оформить графики
Вариант 1: y= –0,1x3–0,16x2+8,04x+11,78
Вариант 2: y= –0,00142x5+0,006x4+0,39x3–1,09x2–2,81x+6,19
Вариант
3:
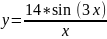
Вариант 4: y=2*(cos(x)+2)^sin(x-2)-2.1;
Вариант 5: y= –0,16x3–0,15x2+7,62x+5,26
Вариант 6: y= –0,00388x5+0,005x4+0,28x3–1,03x2–4,61x+4,78
Вариант
7:
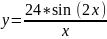
Вариант 8: y= –2*(cos(1,5x)+2,5)sin(x-1)+1.5;
Вариант 9: y= –0,17x3–0,14x2+6,13x+18,48
Вариант 10: y= –0,00258x5+0,01x4+0,22x3–1,11x2–4,63x+7,76
Вариант
11:
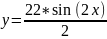
Вариант 12: y=1,2(sin(x)+2,2)cos(x+1)-1.2;
Вариант 13: y= –0,17x3–0,12x2+6,31x+3,83
Вариант 14: y= –0,00367x5+0,005x4+0,23x3–1,06x2–4,39x+8,99
Вариант
15:
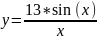
Вариант 16: y=1,4*(0,5cos(2x)+3)sin(x+3)-2;
Вариант 17: y= –0,13x3–0,12x2+6,63x+11,6
Вариант 18: y= –0,00185x5+0,008x4+0,27x3–1,01x2–4,80x+3,56
Вариант
19:
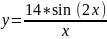
Вариант 20: y=1,3(0,5cos(x)+1,5)atan(x)-1.5;
Вариант 21: y= –0,17x3–0,15x2+9,35x+12,44
Вариант 22: y= –0,00250x5+0,007x4+0,37x3–1,15x2–7,40x+6,59
Вариант
23:
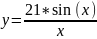
Вариант 24: y=1,4*(cos(3x)+2,8)atan(x+5)-5;
Вариант 25: y= –0,12x3–0,11x2+9,90x+6,64
Вариант 26: y= –0,00333x5+0,005x4+0,25x3–1,20x2–1,39x+2,47
Вариант
27:
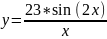
Вариант 28: y=5(0,4*sin(x)+1)atan(x-1)-5.5;
Вариант 29: y= –0,16x3–0,13x2+8,57x+17,30
Вариант 30: y= –0,00167x5+0,005x4+0,35x3–1,13x2–2,12x+4,81
1.2. Задания: построить 2 графика в одном окне, так, чтобы у каждого графика была своя область построения. Оформить графики
Вариант 1. x [–3,5;3,5], шаг 0,5:
y= 2cos(4x)*sin(2x)
z= |cox(x)*sin(x) |
Вариант 2. x [–3,5;3,5], шаг 0,5:
y = |sin(4x)*cos(x)|
z = cos(x)*sin(4x)
Вариант 3. x [–4;4], шаг 1:
y = 2sin(x)
z = 3cos(2x) –sin(x)
Вариант 4. x [–4;4], шаг 0,5:
y = 2sin(5x)cos(4x)
z = sin2(x)
Вариант 5. x [–3,5;3,5], шаг 0,5:
y = 2sin(2x)cos(x)+sin(3x);
z = (1 + x)/(1+ 2x3) при х >1
Вариант 6. x [–2;2], шаг 0,2:
y = 2sin(x)cos(x);
z = 3cos2(x)sin(x).
Вариант 7. x [–3;4], шаг 0,5:
y = 2sin(5x)cos(4x)
z = | cos(x)*sin(x) |
Вариант 8. x [–3,5;3,5], шаг 0,5:
y = (0,25+x3)1/3
y = e-2x
Вариант 9. x [–2;2], шаг 0,2:
y =tn(3x) –sin(2x)
z = sin(x)*cos(x);
Вариант 10. x [–3,5;3,5], шаг 0,5:
y = 3sin(x) – cos2(x)
z =2x3
Вариант 11. x [–5;5], шаг 0,5:
y = ((1+|x|)0,5)/(2+|x|)
z = 2cos2(x)
Вариант 12. x [–2;2], шаг 0,2:
y = ((1 + 2x2)/(1+ x2))0,5
z = (1+x)/(2+cos3(x))
Вариант 13. x [0,1;3], шаг 0,25:
y = e-2x
z= (1+4x)/(2+ln(x))
Вариант 14. x [–2,5;2,5], шаг 0,5:
y = sin(3x)*cos2(x)
z = 2sin(3x) + cos(x)
Вариант 15. x [0;5], шаг 0,5:
y = (0,25+x3)1/3
z = (1+4x)/(2+ln(x))
Вариант 16. x [0;3,6], шаг 0,3:
y = (1 + 2x2)/(3+ 5x2)0,5
y = 3sin(x)*cos(4x)*sin(4x)
Вариант 17. x [–5;5], шаг 0,5:
y = 2cos2(2x)
z = cos3(x) – 4sin(x)
Вариант 18. x [–2;2], шаг 0,1:
y = sin(2x)*cos(3x) – cos2(x)
z = (1 + x)/(1+ 2x3) при х >1
Вариант 19. x [–2,5;2,5], шаг 0,5:
y = 4x + (4+x2)0,5
z = sin(x)*cos(2x)
Вариант 20. x [0;3], шаг 0,25:
y = cos(3x)*sin(x)
z = cos2(x) – cos(3x)
Вариант 21. x [–3;3], шаг 0,2:
y = 4sin(x)
z = 2cos(x)*sin(x)
Вариант 22. x [–5;5], шаг 0,5:
у = 2cos(x) – sin2(3x)
z = | cos(x)*sin(x) |
Вариант 23. x [–3,5;3,5], шаг 0,5:
y = 3sin(3x)*cos(2x)
z = sin(3x)*cos2(x)
Вариант 24. x [–2;2], шаг 0,2:
y = 2cos2(2x) – 3sin(3x)
z = 2sin(3x)
Вариант 25. x [–2,5;2,5], шаг 0,5:
y= 2cos(4x)*sin(2x)
z = (2+x)1/3
Вариант 26. x [0;3,6], шаг 0,3:
y = 3sin(2x)*cos(3x)
z = sin(x)*cos(2x)
Вариант 27. x [–5;5], шаг 0,5:
y = 2sin(3x) + cos(x);
z = 1 + ln(x2 + 1)
Вариант 28. x [0;3], шаг 0,25:
y = 3x3cos(2x)
z = 3sin(x)
Вариант 29. x [–2,5;2,5], шаг 0,5:
y =tn(3x) –sin(2x)
z = sin(x)*cos(6x)
Вариант 30. x [–2;2], шаг 0,2:
у = cos(2x)*sin(3x)
z = cos(2x) – cos(3x)
1.3. Задания: построить поверхности для x [–2,2] и y [–2,2], изменяя значения с шагом 0,5:
Вариант 1. z = x2–2y2
Вариант 2. Z=7x3–6y2
Вариант 3. z=(0,5x–5)2+2(2y–6)2
Вариант 4. z=(0,5x–3)2+(0,5y–3)2
Вариант 5. z=0,5(2x–1)2+0,7(3y–3)2
Вариант 6. z=0,5(2x-5)3+0,5(3y–5)2
Вариант 7. z=(20x–5)2+(4y–5)3
Вариант 8. z=(x-5)2+(y-6)2
Вариант 9. z=3*(x–5)2+3(y–5)2
Вариант 10. z=3(x–5)2+(y–6)2
Вариант 11. z=ex–ey
Вариант 12. z=2х3–3y2
Вариант 13. z = 3x2(y)–5y2
Вариант 14. z = 3x2–2sin2y
Вариант
15.
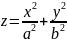 где а=2, b=3
где а=2, b=3
Вариант
16.
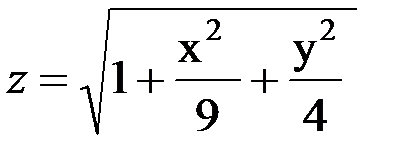
Вариант 17. x2+ y2 + z2 = 42 Сфера
Вариант 18. x2/a2 + y2/b2 - z2/c2 = –1 Гиперболоид а=3, b=2, c=1
Вариант 19. x2/a2 + y2/b2 – z2/c2 = 0 Квадратичный конус. а=3, b=2, c=1
Вариант 20. z=x2–6y2
Вариант
21.
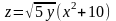
Вариант
22.
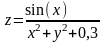
Вариант 23. z=3⋅e−(x−2)2−(y−4)
Вариант 24. z=10x2–5y2
Вариант 25. z=sin(x*y)
Вариант
26.
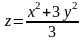
Вариант 27. z=x2–y2–6
Вариант
28.
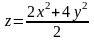
Вариант 29. Z=x3*y–y3*x
Вариант 30. Z=11.83+19.406*x–11.323*y–5.17*x2–4.563*x*y+2.351*y2
