теория 1к 2с / Приближение функций. Методы интерполяции зависимостей с одной независимой переменной. Интерполяционный многочлен Лагранжа. Аппроксимация методом наименьших квадратов
.pdf
Численные методы
Интерполяция и аппроксимация
Интерполяция
Интерполяция - в вычислительной математике
нахождение неизвестных промежуточных значений некоторой функции, по имеющемуся дискретному набору её известных значений, определенным способом.
Методы интерполяции
Интерполяция методом ближайшего соседа
Линейная интерполяция
Интерполяция многочленом Лагранжа
Интерполяция сплайн-функциями 
и др.
Подготовка
Все дальнейшие примеры кода подразумевают, что модуль MatPlotLib и модуль NumPy импортированы следующим образом:
1 import numpy as np
2 import matplotlib.pyplot as plt
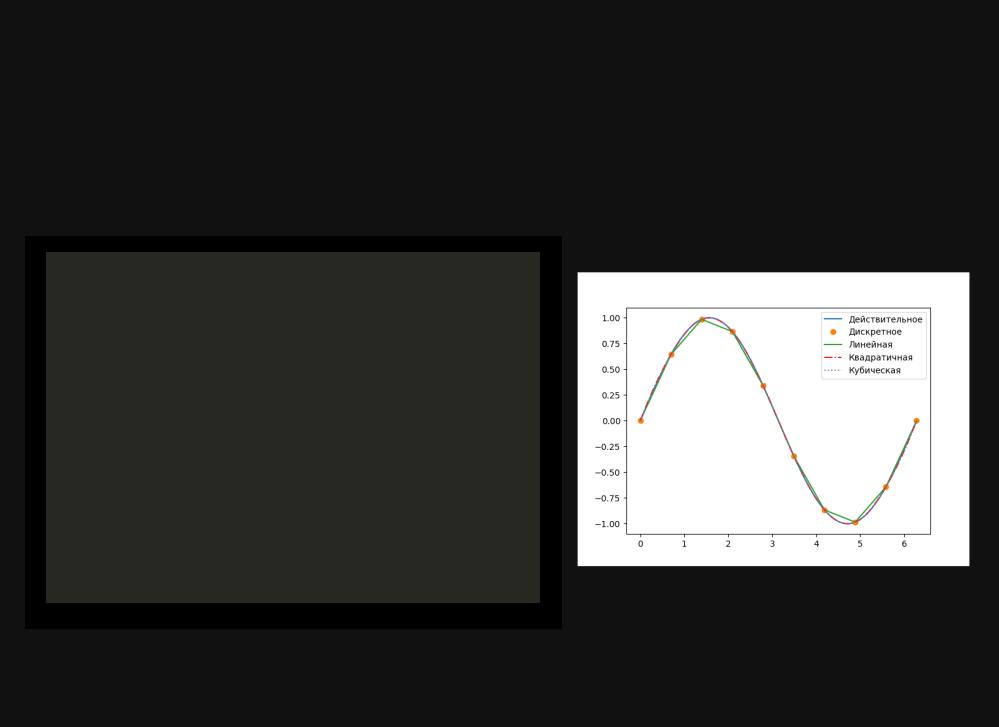
Интерполяция в SciPy
|
Исходный код |
Результат |
1 |
from scipy.interpolate import interp1d |
|
2 |
|
|
3 |
xs = np.linspace(0, 2*np.pi, 1000) |
|
4 |
ys = np.sin(xs) |
|
5 |
|
|
6 |
x = np.linspace(0, 2*np.pi, 10) |
|
7 |
y = np.sin(x) |
|
8 |
|
|
9 |
fl = interp1d(x, y, kind="linear") |
|
10 |
fq = interp1d(x, y, kind="quadratic") |
|
11 |
fc = interp1d(x, y, kind="cubic") |
|
12 |
|
|
13 |
plt.plot(xs, ys, label="Действительное") |
|
14 |
plt.plot(x, y, "o", label="Дискретное") |
|
15 |
plt.plot(xs, fl(xs), ls="-", label="Линейная") |
|
16 |
plt.plot(xs, fq(xs), ls="-.", label="Квадратичная") |
|
17 |
plt.plot(xs, fc(xs), ls=":", label="Кубическая") |
|
18 |
|
|
19plt.legend()
20plt.show()
Интерполяция многочленом Лагранжа
Используйте данный метод только для интерполяции высоко согласованных табличных данных, где может потребоваться
незначительный выход за граничные значения
Математическое выражение
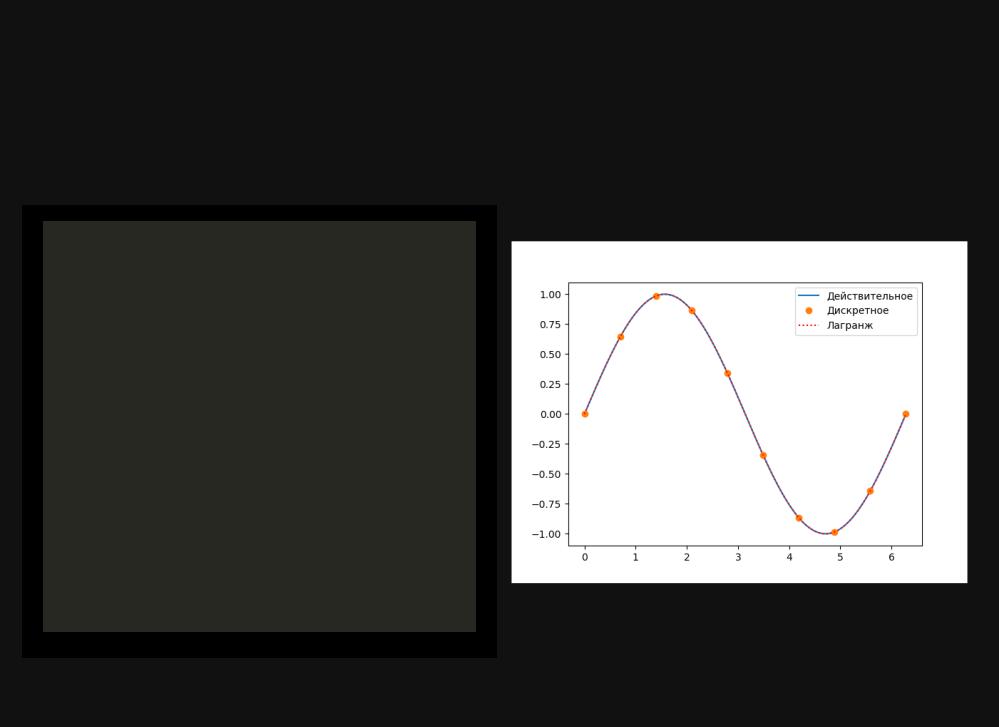
Многочлен Лагранжа
Исходный код |
Результат |
1 def lagrange(x, xs, ys):
2s = 0
3n = len(xs)
4for i in range(n):
5p = 1
6for j in range(n):
7 |
if i == j: continue |
8 |
p *= (x - xs[j]) / (xs[i] - xs[j]) |
9 |
s += ys[i] * p |
10 |
return s |
11 |
|
12 |
xs = np.linspace(0, 2*np.pi, 1000) |
13 |
ys = np.sin(xs) |
14 |
|
15 |
x = np.linspace(0, 2*np.pi, 10) |
16 |
y = np.sin(x) |
17 |
yl = [lagrange(x_, x, y) for x_ in xs] |
18 |
|
19 |
|
20 |
plt.plot(xs, ys, label="Действительное") |
21 |
plt.plot(x, y, "o", label="Дискретное") |
22 |
plt.plot(xs, yl, ls=":", c="r", label="Лагранж") |
23 |
|
24plt.legend()
25plt.show()
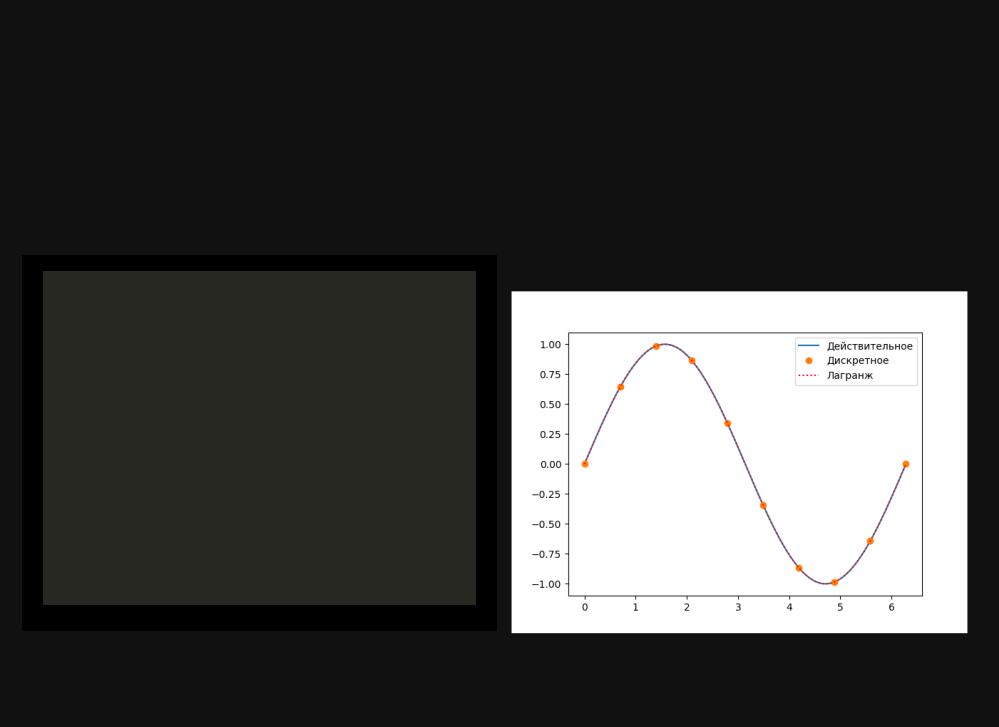
Многочлен Лагранжа
С использованием SciPy
|
Исходный код |
Результат |
1 |
from scipy.interpolate import lagrange |
|
2 |
|
|
3 |
xs = np.linspace(0, 2*np.pi, 1000) |
|
4 |
ys = np.sin(xs) |
|
5 |
|
|
6 |
x = np.linspace(0, 2*np.pi, 10) |
|
7 |
y = np.sin(x) |
|
8 |
|
|
9 |
L = lagrange(x, y) |
|
10 |
|
|
11 |
plt.plot(xs, ys, label="Действительное") |
|
12 |
plt.plot(x, y, "o", label="Дискретное") |
|
13 |
plt.plot(xs, L(xs), ls=":", |
|
14 |
c="r", label="Лагранж") |
|
15 |
|
|
16plt.legend()
17plt.show()