12-2-1

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра Информационных систем

отчет

по домашнему заданию №2

по дисциплине

«Цифровое производство»

Тема: «Модель информационной связности процессов»

№12

Студент гр. 9373		Заболотников М.Е.
Студент гр. 9373		Петрова С.В.
Студент гр. 9373		Романова Е.С.
Преподаватель		Кузнецов А.Г.

Санкт-Петербург

2023

Исходные данные.

Модель:

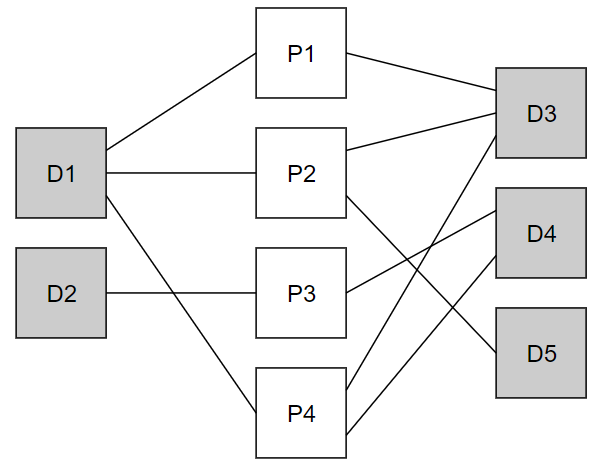
Частота активизации процессов:

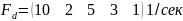
Задание.

Оценить информационную связность процессов:

1. P1, P2, P3, P4;

2. (P1, (P2, P3)), P4;

3. P1, (P2, P3), P4.

Решение.

Составим матрицу 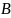– матрицу связей между процессами P1 – P4 и данными D1 – D5:

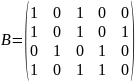
Теперь рассчитаем матрицу 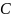– матрицу процессов, совместно использующих данные:

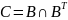
Для того, чтобы учесть число данных D1 – D5, используемых совместно процессами P1 – P4, перемножим матрицы и 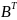стандартным образом:

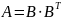
Изобразим матрицу в графическом виде:

Далее найдём матрицу 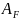частот активизации процессов P1 – P4:

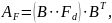
где операция "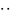 " – поразрядное умножение матрицы на вектор-строку . Итак, получаем:

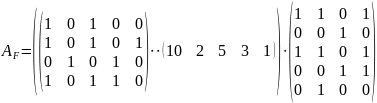
Далее построим матрицу относительных частот активизации процессов путём нормирования матрицы . Для этого разделим элементы каждой строки матрицы на диагональный элемент с соответствующем номером:

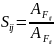
Получим:

Теперь изобразим матрицу в графическом виде:

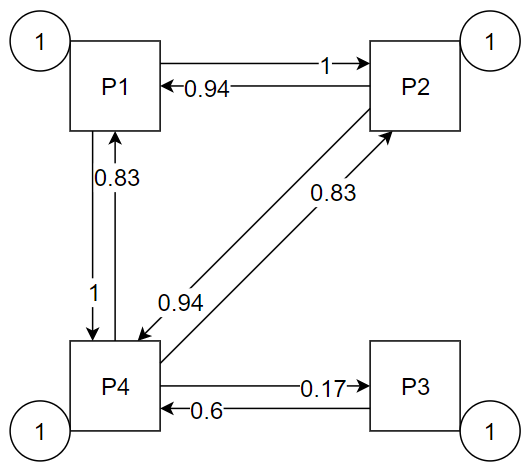
Обозначим как 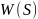сумму всех элементов матрицы , т.е.:

Тогда, зная количество элементов-процессов 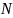, коэффициент связности структуры 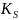рассчитаем по следующей формуле:

Также мы можем найти коэффициенты внутренней и внешней связносте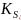й – и :

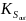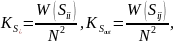
где 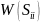– сумма диагональных элементов матрицы , а 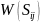– сумма оставшихся элементов. Итак, получаем следующие значения:

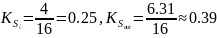
Отсюда мы можем получить относительные коэффициенты внутрен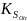ней ( ) и внешне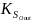й ( ) связей:

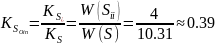
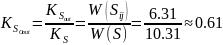
Объединение компонентов в отдельные группы могло бы, предположительно, увеличить относительный коэффициент внутренней связности. Рассмотрим следующий случай объединения: (P1, (P2, P3)), P4. Вот так это примерно выглядит:

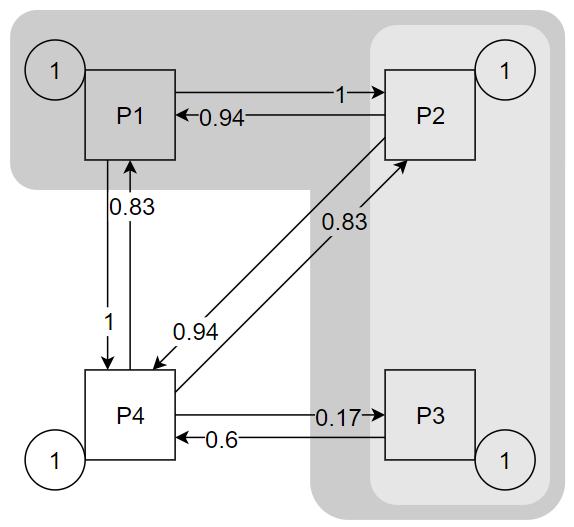
Сначала произведём пересчёт относительных частот активизации процессов P2 и P3:

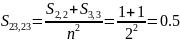
Далее пересчитаем частоты связей с окружением:

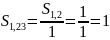
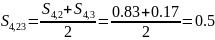
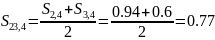
После первого полного пересчёта частот получаем следующую схему:

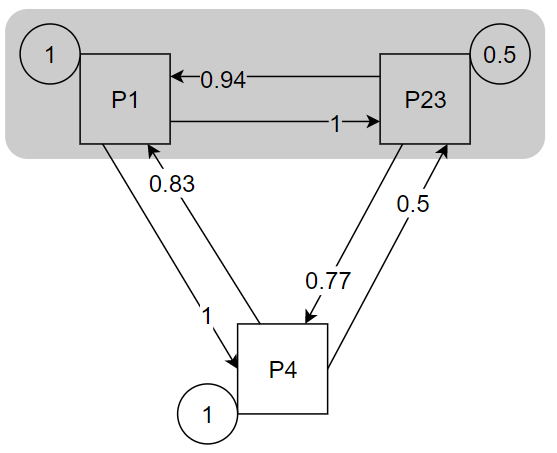
Затем, объединив процессы P1 и P23 и ещё раз пересчитав частоты активизации, получаем схему:

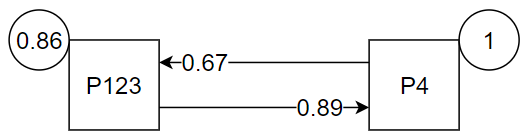
В таком случае матрица относительных частот будет выглядеть следующим образом:

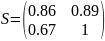
И, соответственно, коэффициенты связности равны:

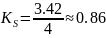
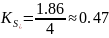
а относительные коэффициенты связности:

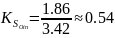
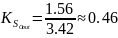
Третий вариант объединения: P1, (P2, P3), P4:

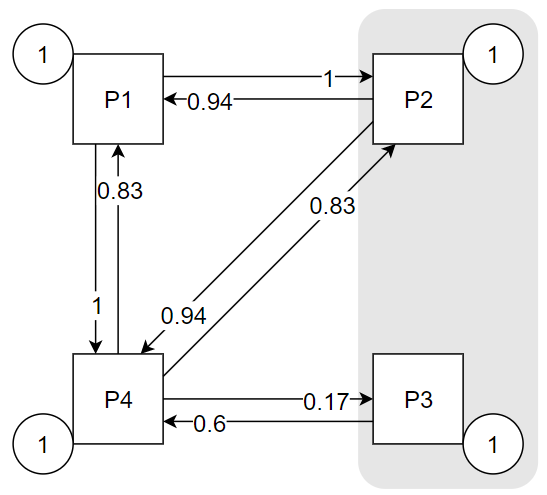
После пересчёта получаем такую схему:

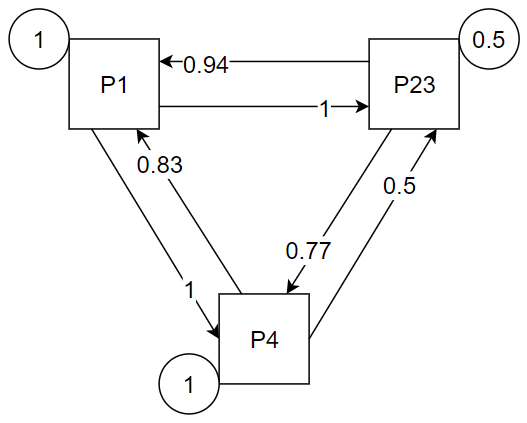
Матрица , соответствующая такой схеме:

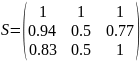
Соответственно, коэффициенты связностей:

Так как 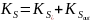, то:

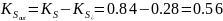
Относительные коэффициенты связности равны:

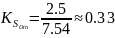
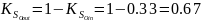
Итого, имеем следующие показатели связности при различных конфигурациях модели функциональной связности:

№	Вид объединения
1	P1, P2, P3, P4	0.64	0.25	0.39
2	(P1, (P2, P3)), P4	0.86	0.47	0.54
3	P1, (P2, P3), P4	0.84	0.28	0.33

Лист ошибок и замечаний.