4.7.2. Классификация задач с точки зрения планируемости
Тест, который определяет, может ли множество готовых задач быть спланированным таким образом, что каждая задача завершится в заданный для нее предельный срок, называется тестом планируемости.
Разработка тестов планируемости чрезвычайно сложная проблема.
По количеству временной информации, используемой для планирования, задачи делятся на периодические, спорадические и апериодические.
Для периодической задачи, начиная с момента времени первого запроса на выполнение, известны все последующие моменты запросов (на основе добавления известного периода к моменту начального запроса).
Обозначим через pi период i-й задачи, через ci – время выполнения i-й задачи. Тогда условие планируемости формулируется следующим образом:
Множество периодических задач планируемо, если
m = mi = ci/pi <= 1
Отношение mi = ci/pi называется фактором полезности i-й задачи и обозначает долю времени, которую i-я задача требует сервиса от процессора.
Кроме перечисленных временных параметров используют следующие параметры:
di – предельный интервал завершения – разность между предельным сроком завершения и временем запроса;
li – неопределенность задачи – разность между di и ci.
Для спорадической задачи времена запроса не известны априори.
Чтобы хоть как-то решить задачу планирования, необходимо задать минимальный интервал между парой запросов для каждой из спорадических задач.
Для апериодической задачи вообще нет никаких ограничений на моменты запросов.
Для решения проблемы планирования чрезвычайно важно знание будущего поведения задач.
Если планировщик не имеет сведений о будущих моментах запросов спорадической задачи, то проблема планирования не разрешима.
Т.е. для разрешения проблемы планирования должны быть сделаны предположения о будущих моментах запросов.
4.7.3. Динамическое планирование
По каждому событию, приводящему к запуску планирующего алгоритма, динамический планировщик оперативно определяет, какая задача из множества готовых задач должна быть обслужена следующей.
Алгоритмы различаются предположениями о характере поведения задач.
4.7.3.1. Планирование независимых задач
Алгоритмы без использования приоритетов
К указанным алгоритмам относятся:
Алгоритм планирования по принципу FIFO;
Алгоритм циклического планирования;
Алгоритм многоуровневого планирования.
Планирование по принципу FIFO. Это простейшая дисциплина обслуживания без вытеснения.
В чистом виде используется редко. Используется в сочетании с другими дисциплинами обслуживания.
Эта дисциплина бесполезна в случае интерактивных задач, поскольку не может гарантировать хорошие показатели времени отклика.
Циклическое или круговое планирование (RR – round robin).
Сочетание принципа FIFO с time-sharing-ом.
Если процесс не заканчивает выполнение в течение выделенного кванта времени, он снимается с процессора и ставится в конец очереди.
Такой вариант планирования может использоваться и без time-sharing-га.
В этом случае процесс снимается с процессора и ставится в конец очереди при обращении к примитивам ядра или при добровольной передаче управления.
Так реализовано планирование в NetWare 3 и оно очень эффективно.
Такая дисциплина может быть использована с интерактивными процессами.
Многоуровневое планирование.
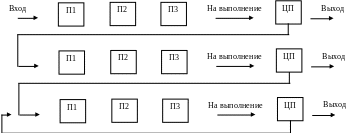
Процесс входит в сеть очередей с самого верхнего уровня.
Перемещается по очереди, пока не достигнет процессора.
Если выделенный квант времени истекает, то процесс снимается с выполнения и переводится в следующую очередь.
И т. д.
На самом низу - циклическое обслуживание до завершения.
Квант времени с переходом на более низкий уровень увеличивается.
Процессы из очереди некоторого уровня начинают выполняться, если нет процессов в очередях более высоких уровней, и прерываются, если появляются процессы на более высоких уровнях.
В некоторых системах процесс несколько раз проходит по очереди одного уровня прежде, чем попадает в очередь более низкого уровня.
И количество таких циклов растет с переходом на более низкие уровни.
Многоуровневые очереди - идеальный механизм планирования.
Цель перечисления этих вариантов планирования состоит в том, чтобы показать важность оценки потерь при выборе тех или иных алгоритмов планирования для многозадачной операционной среды.
Алгоритмы приоритетного планирования