
Лаб9_отчёт
.doc
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ИС
отчет
по лабораторной работе №9
по дисциплине «Конструирование программ»
Тема: Решение систем линейных алгебраических уравнений методом простых итераций
Студент гр. 9373 |
|
Заболотников М.Е. |
Преподаватель |
|
Копыльцов А.В. |
Санкт-Петербург
2021
Цель работы.
Методом
простых итераций с точностью
![]() решить систему линейных алгебраических
уравнений, заданную в форме
решить систему линейных алгебраических
уравнений, заданную в форме
![]() .
.
Основные теоретические положения.
Итерационные методы применяют главным образом для решения задач большой размерности, когда использование прямых методов невозможно из-за ограничений технического характера. Большие системы уравнений, возникающие в приложениях, как правило, являются разреженными. При использовании метода Гаусса, например, большое число нулевых элементов превращаются в ненулевые и матрица теряет свойство разреженности. Использование итерационных методов не меняет матрицу коэффициентов, она остается разреженной.
Однако применение итерационных методов для качественного решения требует серьезного использования структуры системы уравнений, специальных знаний и опыта.
Пусть
дана система
![]() -
квадратная невырожденная матрица.
Преобразуем ее к виду
-
квадратная невырожденная матрица.
Преобразуем ее к виду
![]() (5.5.1)
(5.5.1)
где
![]() -
квадратная матрица такой же размерности
что и
-
квадратная матрица такой же размерности
что и
![]() ,
,
![]() -
вектор -столбец. В развернутой форме
записи система (5.5.1) имеет вид
-
вектор -столбец. В развернутой форме
записи система (5.5.1) имеет вид
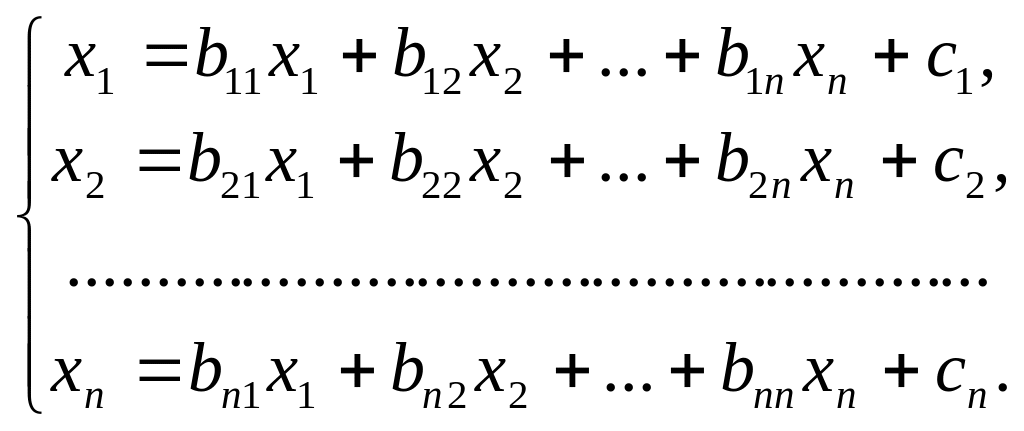 (5.5.2)
(5.5.2)
Операция
приведения системы
![]() к виду (5.5.2) не является очевидной и
простой и требует специальных знаний,
а также существенного использования
специфики системы. Самый простой способ
приведения системы
к виду (5.5.2) состоит в последовательном
исключении из первого уравнения системы
переменной
к виду (5.5.2) не является очевидной и
простой и требует специальных знаний,
а также существенного использования
специфики системы. Самый простой способ
приведения системы
к виду (5.5.2) состоит в последовательном
исключении из первого уравнения системы
переменной
![]() ,
из второго уравнения - переменной
,
из второго уравнения - переменной
![]() и так далее. Метод итерации в такой
реализации называется методом Якоби.
Система уравнений метода Якоби имеет
вид
и так далее. Метод итерации в такой
реализации называется методом Якоби.
Система уравнений метода Якоби имеет
вид
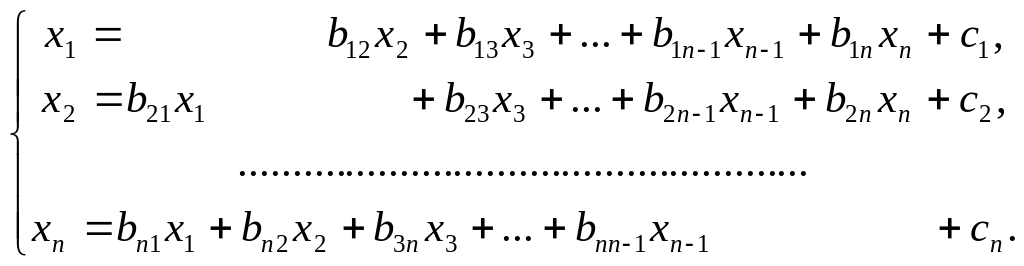 (5.5.3)
(5.5.3)
На
главной диагонали матрицы
системы (5.5.3) стоят нули, а остальные
элементы, очевидно, выражаются по
формулам
![]()
Практически
метод работает следующим способом.
Выбирается начальное приближение
![]() и подставляется в правую часть системы
(5.5.1). Решая систему, находят первое
приближение
и подставляется в правую часть системы
(5.5.1). Решая систему, находят первое
приближение
![]() Это приближение опять подставляют в
правую часть (5.5.1). Таким образом,
получается
Это приближение опять подставляют в
правую часть (5.5.1). Таким образом,
получается
![]() Продолжая этот процесс далее, получим
последовательность
Продолжая этот процесс далее, получим
последовательность
![]() приближений, вычисляемых по формуле
приближений, вычисляемых по формуле
![]() (5.5.4)
(5.5.4)
В развернутой форме записи система (5.5.4) выглядит таким образом:
 (5.5.5)
(5.5.5)
5.6. Сходимость метода простых итераций
Теорема
5.4. Пусть
![]() Тогда решение
Тогда решение
![]() системы
системы
![]() существует и единственно. При любом
начальном приближении
существует и единственно. При любом
начальном приближении
![]() метод простых итераций сходится и
справедлива оценка погрешности
метод простых итераций сходится и
справедлива оценка погрешности
![]() (5.6.1)
(5.6.1)
Доказательство
Пусть
в (5.5.5)
![]() тогда
тогда
![]() Если
-
точное решение системы, то оно удовлетворяет
уравнению (5.5.1), то есть
Если
-
точное решение системы, то оно удовлетворяет
уравнению (5.5.1), то есть
![]() .
Вычтем два последних уравнения друг из
друга. Получим
.
Вычтем два последних уравнения друг из
друга. Получим
![]() Найдем норму этого выражения:
Найдем норму этого выражения:
![]()
![]() ,
так как неравенство верно для всех
индексов от 0 до
,
так как неравенство верно для всех
индексов от 0 до
![]() .
.
Итак,
метод простых итераций сходится со
скоростью геометрической прогрессии,
знаменатель которой
![]() Скорость сходимости тем выше, чем меньше
величина
Скорость сходимости тем выше, чем меньше
величина
![]() .
Хотя метод сходится при любом начальном
приближении
,
ясно, что начальное приближение нужно
выбирать ближе к точному решению.
Приведенная в теореме 5.4 оценка точности
решения является априорной. Ее практическое
использование затруднительно, так как
.
Хотя метод сходится при любом начальном
приближении
,
ясно, что начальное приближение нужно
выбирать ближе к точному решению.
Приведенная в теореме 5.4 оценка точности
решения является априорной. Ее практическое
использование затруднительно, так как
![]() неизвестно, а его грубое оценивание
заведомо приведет к завышению числа
итераций
.
неизвестно, а его грубое оценивание
заведомо приведет к завышению числа
итераций
.
Теорема 5.5. (Апостериорная оценка погрешности решения).
Если
![]() ,
то справедлива следующая оценка:
,
то справедлива следующая оценка:
![]() (5.6.2)
(5.6.2)
Доказательство
В
предыдущей теореме имели равенство
![]() Преобразуем
его алгебраически:
Преобразуем
его алгебраически:
![]() .
Тогда
.
Тогда
![]() Отсюда легко получаем
Отсюда легко получаем
![]()
Если
требуется найти решение с точностью
![]() ,
то следует проводить итерации до
выполнения неравенства
,
то следует проводить итерации до
выполнения неравенства
![]() Таким образом, в качестве критерия
окончания итерационного процесса может
быть использовано неравенство
Таким образом, в качестве критерия
окончания итерационного процесса может
быть использовано неравенство
![]()
Экспериментальные результаты.
Экспериментальные данные были взяты из методических указаний и представлены в виде таблицы на рисунке 1:

Рис. 1. Экспериментальные данные.
Обработка результатов эксперимента.
Для обработки полученных данных была написана программа, которая выполняет поставленную задачу и решает систему линейных алгебраических уравнений, заданную в форме , методом простых итераций с точностью . Результат работы программы представлен на рисунке 2:
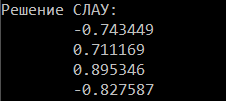
Рис. 2. Иллюстрация результата работы программы.
Выводы.
В ходе выполнения работы был изучен метод обратных итераций по решению систем линейных алгебраических уравнений и написана программа, которая выполняет поставленную задачу.
Карл Густав Якоб Якоби (1804-1851 ) - немецкий математик.
