Лаб8_отчёт

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ИС

отчет

по лабораторной работе №8

по дисциплине «Конструирование программ»

Тема: Вычисление собственных значений (чисел) и векторов матриц.

Студент гр. 9373		Заболотников М.Е.
Преподаватель		Копыльцов А.В.

Санкт-Петербург

2021

Цель работы.

Найти максимальное по модулю собственное число и соответствующий ему собственный вектор матрицы .

Основные теоретические положения.

Пусть необходимо вычислить максимальное по модулю собственное число , матрицы  , причем В степенном методе используется следующая последовательность формул. Выбирается произвольный начальный вектор и строится последовательность векторов и приближений к собственному числу таким образом:

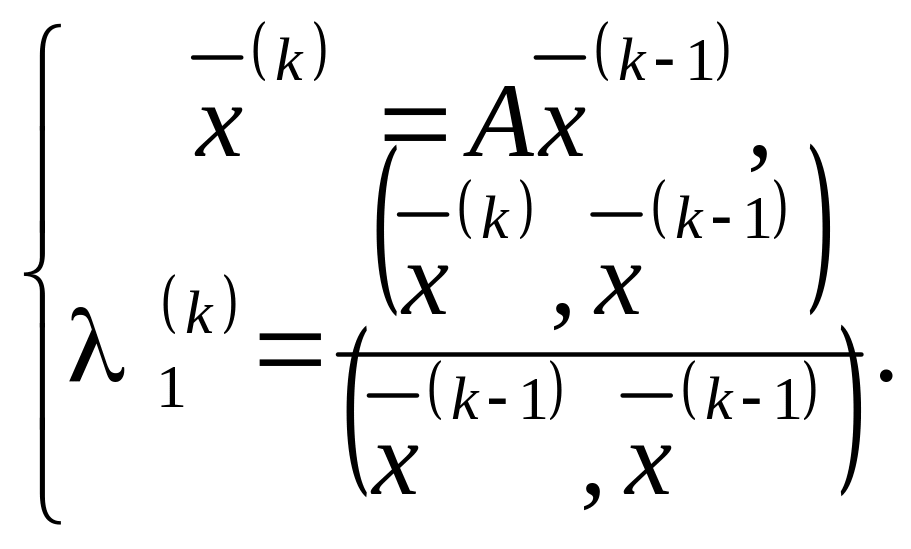(5.13.1)

Правая часть формулы для в (5.13.1) - это отношение Релея при Так как то

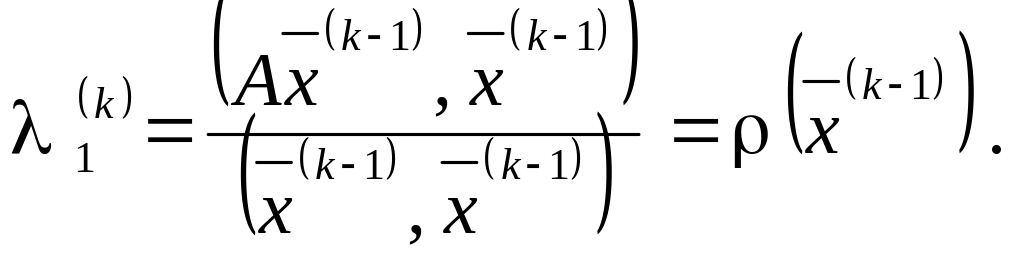
Теорема 5.11. Пусть в разложении по базису из собственных векторов произвольной матрицы , собственные числа которой удовлетворяют условию и Тогда при и справедлива следующая оценка погрешности:

(5.13.2)

При практических вычислениях вектор нормируют, чтобы не было переполнения или исчезновений порядка. Формулы (5.13.1) тогда приобретают вид

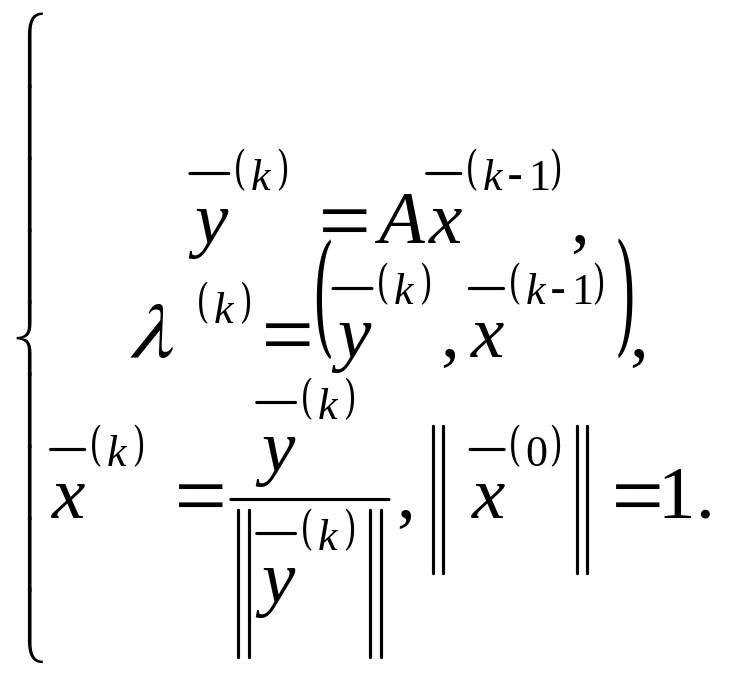(5.13.3)

В общем случае при решении проблемы собственных значений не существует эффективных апостериорных оценок погрешностей. Для симметрических матриц можно использовать следующий результат.

Теорема 5.12. Пусть - произвольное число, а - произвольный ненулевой вектор. Тогда для любой симметрической матрицы существует собственное число такое, что справедлива оценка

(5.13.4)

В частности для степенного метода, если - приближенно вычисленный собственный вектор, а - приближенное значение собственного числа, то

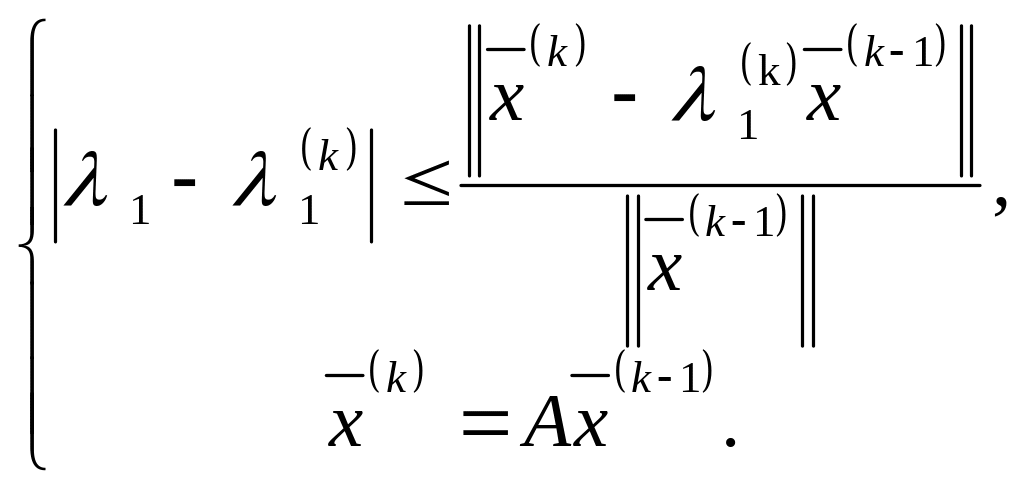(5.13.5)

Пример. Для матрицы из предыдущего примера вычислить и , взяв в качестве начального приближения

Вычисления будем производить по формулам (5.13.3):

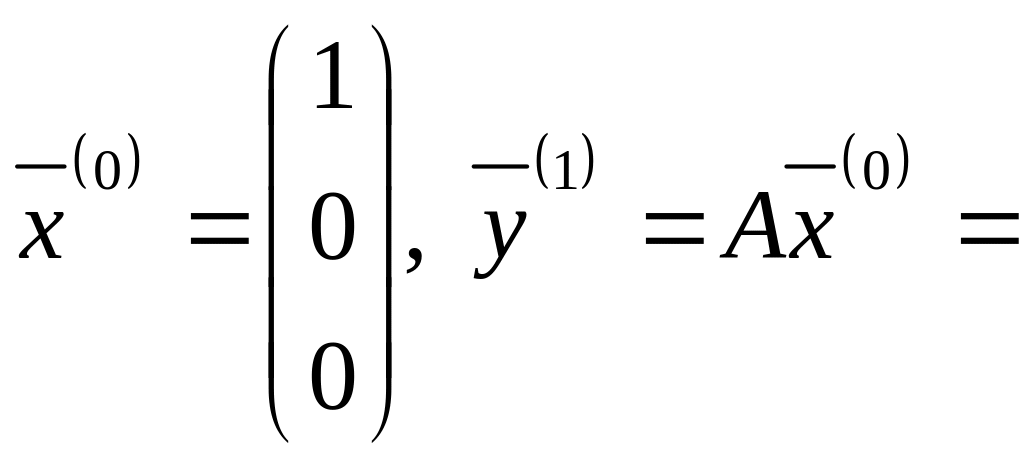
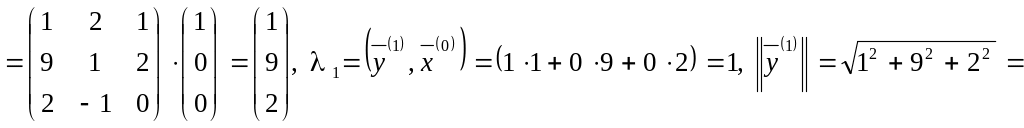
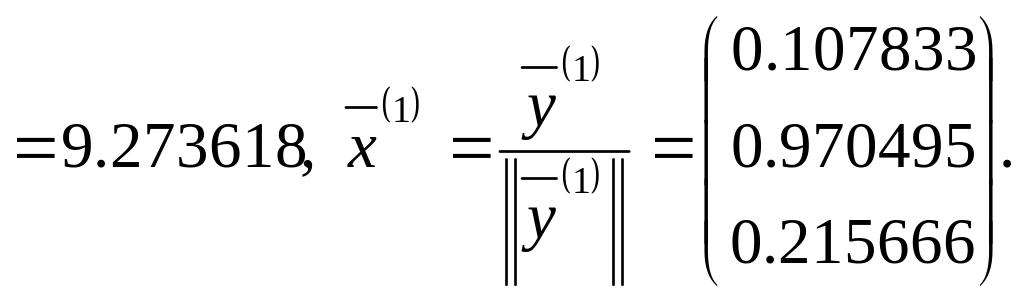Результаты вычислений шестнадцати итераций приведены в следующей таблице:

Номер итерации
0	-	1.0000000	0.000000	0.000000
1	1	0.107833	0.970945	0.215666
2	2.401193	0.670351	0.707602	-0.223450
3	5.560346	0.282393	0.954482	0.096011
4	4.128699	0.524958	0.846417	-0.089436
5	5.375470	0.320293	0.811308	-0.051321
6	4.703964	0.461342	0.886644	-0.032067
7	5.425668	0.404845	0.914362	0.006624
8	5.085983	0.439969	0.897778	-0.020557
9	5.298928	0.417814	0.908526	-0.002034
10	5.171134	0.431704	0.901906	-0.014094
11	5.251758	0.422957	0.906120	-0.007328
12	5.226316	0.426272	0.904522	-0.011520
13	5.216012	0.426340	0.904508	-0.009965
14	5.220049	0.426316	0.904519	-0.009929
15	5.219940	0.426331	0.904513	-0.009940
16	5.220039	0.426322	0.904517	-0.009933

Видно, что при вычислении по формуле Кардано не достигнута даже точность , так как , а не 5.242, как в предыдущем примере. Главный недостаток этого метода - медленная сходимость, пропорциональная .

Для вычисления следующего собственного числа можно использовать сдвиг на . После сдвига рассматривается матрица , собственными числами которой являются числа . В этом случае число будет минимальным по модулю, следовательно, степенной метод даст другое число, например, , сдвиг которого максимален.

Экспериментальные результаты.

Экспериментальные результаты были взяты из методических указаний и представлены в виде матрице на рисунке 1:

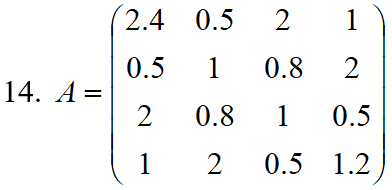
Рис. 1. Матрица А.

Обработка результатов эксперимента.

Для обработки экспериментальных данных была создана программа, которая находит максимальное по модулю собственное число и соответствующий ему собственный вектор матрицы . Результат программа представлен на рисунке 2:

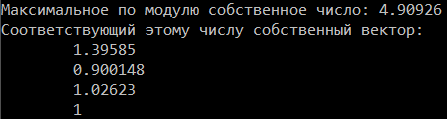
Рис. 2. Иллюстрация результата работы программы.

Выводы.

В ходе работы была написана программа, которая находит максимальное по модулю собственное число и соответствующий ему собственный вектор матрицы .

5