Лаб7_отчёт

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ИС

отчет

по лабораторной работе №7

по дисциплине «Конструирование программ»

Тема: Методы интегрирования обыкновенных дифференциальных уравнений

Студент гр. 9373		Заболотников М.Е.
Преподаватель		Копыльцов А.В.

Санкт-Петербург

2021

Цель работы.

Изучить методы Эйлера и Рунге-Кутты по решению СНАУ и решить заданное дифференциальное уравнение первого порядка методом Эйлера и Рунге – Кутты четвертого порядка на отрезке с шагом .

Основные теоретические положения.

Методы Рунге - Кутты обладают следующими отличительными свойствами:

1) являются одношаговыми: чтобы найти нужна информация только о предыдущей точке ;

2) согласуются с рядом Тейлора вплоть до членов порядка , где степень различна для различных методов и называется порядком метода;

3) не требуют вычисления производных от , а только вычисления функции.

Именно благодаря третьему свойству методы Рунге - Кутты более известны, нежели ряд Тейлора. Однако для вычисления одной последующей точки решения приходится вычислять несколько раз при различных значениях

В ыведем сначала некоторые формулы на основе геометрических аналогий.

Пусть известна точка на искомой кривой. Через эту точку можно провести прямую с тангенсом угла наклона Тогда следующей можно считать точку, где прямая пересечет ординату, проведенную через точку Уравнение прямой имеет вид но так как , то (7.4.1)

Формула (7.4.1) описывает метод Эйлера^, один из самых старых и широко известных методов численного интегрирования дифференциальных уравнений. Формула (7.4.1) может быть получена из (7.2.2), если принять . Так как здесь функция не зависит от , то метод является явным.

Ошибка интегрирования при показана на рисунке в виде отрезка . Очевидно, что найденное таким образом приближенное решение согласуется с разложением в ряд Тейлора вплоть до членов порядка , так что ошибка равна

Теорема 7.2. Пусть функция удовлетворяет условию Тогда справедливо неравенство

(7.4.2)

то есть метод Эйлера устойчив на конечном отрезке. Здесь - погрешность аппроксимации дискретного уравнения (7.2.1) на решении .

Метод Эйлера, реализуемый формулой (7.4.1), можно усовершенствовать множеством различных способов. Рассмотрим две модификации: а) исправленный метод Эйлера и б) модифицированный метод Эйлера.

а). В исправленном методе Эйлера находим средний тангенс угла наклона касательной для двух точек и . Геометрически процесс нахождения точки можно проследить по левому рисунку на следующей странице. С помощью метода Эйлера находится точка , лежащая на прямой . В этой точке снова вычисляется тангенс угла наклона касательной, на рисунке этому значению соответствует прямая . Усреднение двух тангенсов дает прямую . Наконец, через точку проводим прямую , параллельную . Точка, в которой прямая пересечется с ординатой и будет искомой точкой .

а) б)

Тангенс угла наклона прямой равен:

(7.4.3)

Уравнение при этом записывается в виде Таким образом,

. (7.4.4)

Это и есть рабочее уравнение исправленного метода Эйлера.

Выясним, как хорошо этот метод согласуется с разложением в ряд Тейлора. Для этого запишем разложение в ряд Тейлора для функции двух переменных в окрестности точки : Если положить здесь то получим

Подставляя этот результат в (7.4.3) и производя необходимые преобразования, будем иметь что совпадает с (7.3.2) вплоть до членов степени h². Таким образом, исправленный метод Эйлера является методом Рунге - Кутты второго порядка.

б). Если в рассмотренном методе усреднялись наклоны касательных, то в модифицированном методе Эйлера усредняются точки (смотрите рисунок справа). Первоначальное построение сделано точно так же, как и в предыдущем случае - через точку проведена прямая с тангенсом угла наклона, равным . Затем взята точка на пересечении этой прямой и ординаты Угол наклона касательной в этой точке

(7.4.5)

Проведем через точку прямую , параллельную . Пересечение этой прямой с ординатой и даст искомую точку . Так как уравнение прямой можно записать в виде , то

(7.4.6)

Формула (7.4.6) описывает модифицированный метод Эйлера.

В литературе исправленный метод Эйлера называют иногда методом Эйлера - Коши^, а модифицированный метод - усовершенствованным. Как и в предыдущем случае, можно легко показать, что модифицированный метод является методом Рунге - Кутты второго порядка.

Оба рассмотренных метода описываются формулами вида , причем в обоих случаях функция имеет вид

(7.4.7)

Для исправленного метода Эйлера а для модифицированного

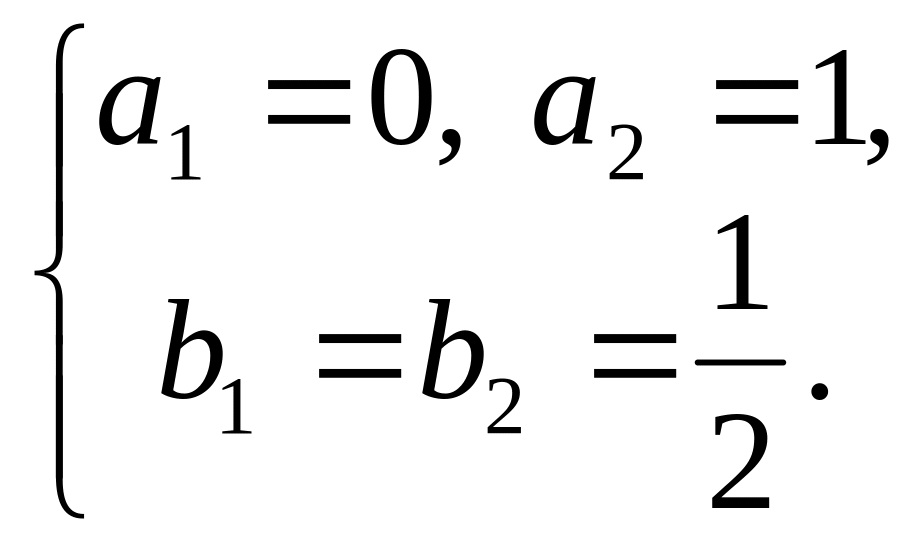
Методы Рунге - Кутты третьего и четвертого порядков можно вывести совершенно аналогично тому, как это делалось при выводе методов первого и второго порядков. Общая идея вывода формулы метода Рунге - Кутты любого заданного порядка состоит в следующем.

Пусть - решение дифференциального уравнения удовлетворяющее условию Проинтегрируем уравнение по от до , получим По формуле Ньютона - Лейбница^

Тогда (7.4.8)

Если бы интеграл в формуле (7.4.8) вычислялся точно, то она была бы основной рабочей формулой всех методов численного интегрирования дифференциальных уравнений. В действительности используют приближенную формулу, заменяя интеграл квадратурной суммой.

Введем на отрезке вспомогательных узлов , ,..., , где Тогда интеграл в уравнении (7.4.8) можно заменить квадратурной суммой с узлами то есть

(7.4.9)

Здесь неизвестны значения Применяя формулу (7.4.8), получим

Заменим для каждого входящий в эту формулу интеграл соответствующей ему квадратурной суммой с узлами :

(7.4.10)

Формулы (7.4.10) позволяют последовательно вычислять приближения к значениям Пусть Тогда формулу (7.4.8) можно переписать в виде

(7.4.11)

Если исключить отсюда величины , получим

(7.4.12)

Выбор конкретных значений параметров осуществляется по-разному и дает ту или иную модификацию методов Рунге - Кутты. Приведем рабочие формулы метода четвертого порядка. Он применяется настолько широко, что в литературе называется просто «методом Рунге - Кутты» без всяких указаний на тип или порядок. Этот классический метод Рунге - Кутты описывается системой следующих шести уравнений:

(7.4.13)

Ошибка метода при его использовании функцию необходимо вычислять дважды.

Экспериментальные результаты.

Экспериментальные данные были взяты из методических указаний и представлены на рисунке 1:

Рис. 1.

Обработка результатов эксперимента.

Для обработки экспериментальных данных была написана программа, которая решает заданное дифференциальное уравнение первого порядка методом Эйлера и Рунге – Кутты четвертого порядка на отрезке с шагом . Результат работы программы представлен на рисунке 2:

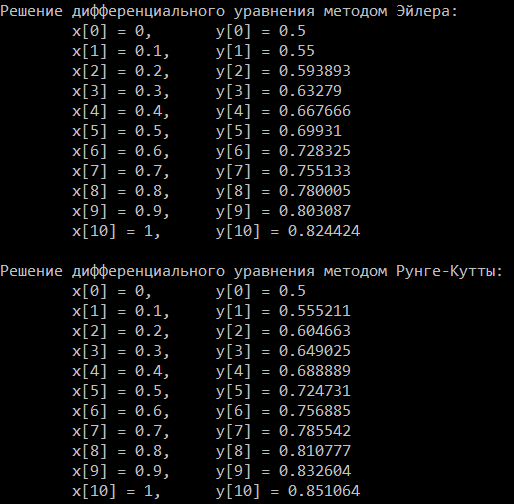
Рис. 2. Результат работы программы.

Выводы.

В ходе работы были изучены методы Эйлера и Рунге-Кутты по решению дифференциальных уравнений и написана программа, которая реализует эти два метода и решает поставленную задачу.

 Леонард Эйлер (1707-1783) - швейцарский математик. Долгое время жил и работал в России.

 Огюст Луи Коши (1789-1857.) - французский математик.

^ Готфрид Вильгельм Лейбниц (1646 - 1716.) - немецкий математик, создатель дифференциального исчисления.

9