
Лаб3_отчёт
.doc
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ИС
отчет
по лабораторной работе №3 (вариант 14)
по дисциплине «Конструирование программ»
Тема: Интерполирование и экстраполирование данных. Интерполяционный многочлен Лагранжа. Схема Эйткена.
Студент гр. 9373 |
|
Заболотников М.Е. |
Преподаватель |
|
Копыльцов А.В. |
Санкт-Петербург
2021
Цель работы.
Познакомиться с таким понятием, как интерполяционный многочлен Лагранжа и по заданию вычислить приближённое значение многочлена Лагранжа при данном значении аргумента, используя схему Эйткена.
Основные теоретические положения.
Согласно этой схеме интерполяционные многочлены любого вида вычисляются последовательно по формулам
 (2.8.1)
(2.8.1)
и
так далее. Интерполяционный многочлен
![]() -й
степени, принимающий в точках
-й
степени, принимающий в точках
![]() значения
значения
![]() запишется следующим образом:
запишется следующим образом:
![]() (2.8.2)
(2.8.2)
Действительно,
из первой формулы (2.8.1) при
![]() сразу
получаем
сразу
получаем
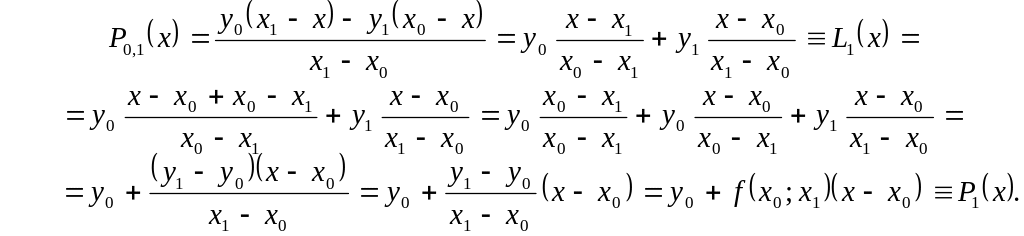
Остальные
формулы проверяются аналогично. Кроме
того, мы получили, что
![]() .
Это действительно так по теореме о
единственности интерполяционного
многочлена
-й
степени. Таким образом,
.
Это действительно так по теореме о
единственности интерполяционного
многочлена
-й
степени. Таким образом,
![]() тождественно совпадают и являются по
сути лишь разной
формой записи единого интерполяционного
многочлена
-й
степени.
тождественно совпадают и являются по
сути лишь разной
формой записи единого интерполяционного
многочлена
-й
степени.
Схема
Эйткена применяется там, где не нужно
общее выражение
![]() ,
а нужно лишь его значение при конкретных
,
а нужно лишь его значение при конкретных
![]() ,
и при этом значения функции даны в
достаточно большом числе узлов. Вычисления
по схеме Эйткена удобно вести с помощью
таблицы, аналогичной таблице конечных
или разделенных разностей:
,
и при этом значения функции даны в
достаточно большом числе узлов. Вычисления
по схеме Эйткена удобно вести с помощью
таблицы, аналогичной таблице конечных
или разделенных разностей:
-



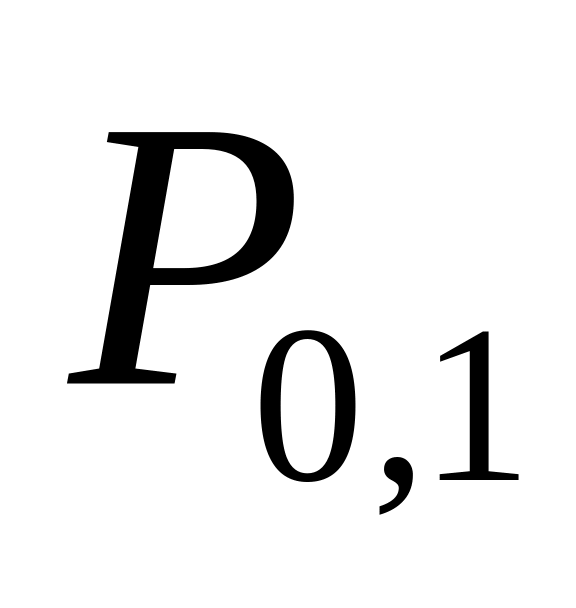











 ...
......


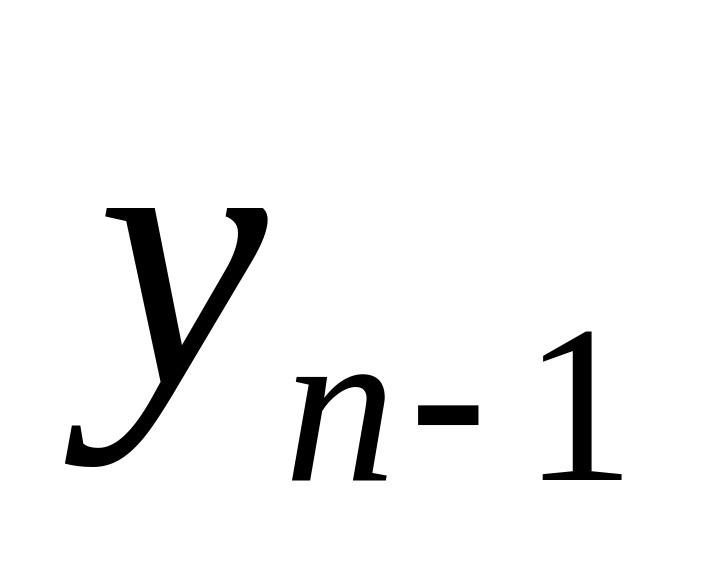




Вычисления
прекращают, если
![]() или если последовательные значения
или если последовательные значения
![]() совпадут в пределах заданной точности.
совпадут в пределах заданной точности.
Экспериментальные результаты.
Экспериментальные данные были взяты из методических указаний и представлены в виде таблицы (см. рис.1):
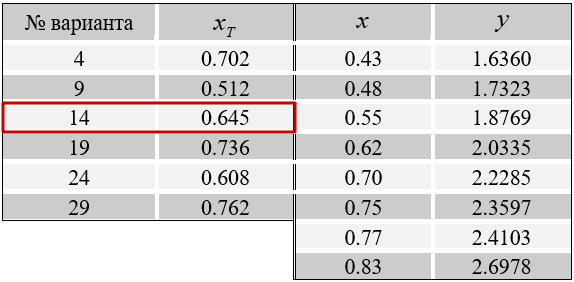
Рис. 1. Иллюстрация экспериментальных данных (красным выделена строк, соответствующая вариату данной работы).
Обработка результатов эксперимента.
Для обработки исходных данных была написана программа, вычисляющая приближённое значение функции у = f(x) по схеме Эйткена. Результат работы программы представлены на рис. 2:
![]()
Рис. 2. Результат работы программы.
Выводы.
В ходе работы было изучено такое понятие, как интерполяционный многочлен Лагранжа, а также была написана и отработана программа по вычислению приближённого значения функции у = f(x).
