
Лаб1_отчёт
.doc
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ИС
отчет
по лабораторной работе №1 (вариант 14)
по дисциплине «Конструирование программ»
Тема: Определение абсолютной и относительной погрешностей приближенных чисел. Оценка погрешностей результата.
Студент гр. 9373 |
|
Заболотников М.Е. |
Преподаватель |
|
Копыльцов А.В. |
Санкт-Петербург
2021
Цель работы.
Познакомиться с понятием абсолютной и относительной погрешностей функции через расчёты соответствующих величин для данной в задании функции.
Основные теоретические положения.
Пусть
![]() - функция
- функция
![]() -
переменных, дифференцируемая в
рассматриваемой области (например, на
отрезке
-
переменных, дифференцируемая в
рассматриваемой области (например, на
отрезке
![]() ).
).
Теорема
1.7. Для
абсолютной погрешности значения
![]() справедлива следующая формула:
справедлива следующая формула:
![]() . (1.4.1)
. (1.4.1)
Доказательство
Вспомним
сначала формулу Тейлора
для функции нескольких переменных. Для
функции одного переменного разложение
в окрестности точки
![]() будет иметь вид
будет иметь вид
![]()
Для функции переменных форма записи формулы Тейлора остается точно такой же, если вместо производных записать дифференциалы соответствующих порядков:
![]()
где,
![]() .
Например, для функции двух переменных
.
Например, для функции двух переменных
![]()

Отбрасывая все члены второго порядка и выше, получим
![]()
Таким
образом, искомая формула сразу вытекает
из формулы Лагранжа1.
Если
![]() достаточно мало, то для предельных
значений погрешностей можно положить
достаточно мало, то для предельных
значений погрешностей можно положить
![]()
Для относительных погрешностей тогда имеем следующие формулы:

Экспериментальные результаты.
Для первой части лабораторной работы экспериментальные данные были получены из методических указаний и представлены в виде таблицы (см. рис. 1):
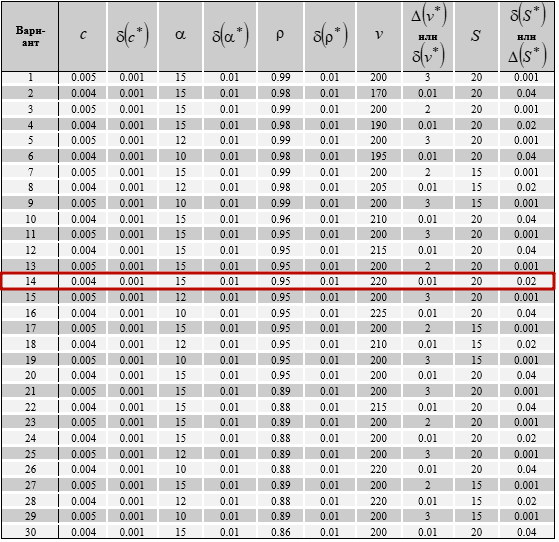
Рис. 1. Экспериментальные данные (для данного варинта нужная строка выделена красным).
Данные для второй части работы представлены в таблице (см. рис. 2):
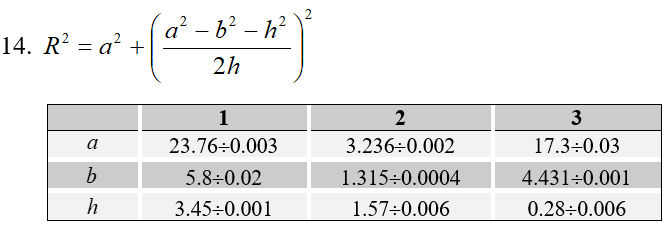
Обработка результатов эксперимента.
На основе полученных экспериментальных данных была написана программ, производящая расчёты по вычислению:
а) значения функции F и отностельной погрешноти F (см. рис. 3);
б) абсолютной погрешности значения функции при заданных знчениях аргументов при трёх опытах (см. рис. 4).
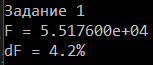
Рис. 3. Выполнение первой части работы.

Рис. 4. Выполнение второй части работы.
Выводы.
В ходе выполнения данной лабораторной работы было произведено ознакомление с такими понятиями, как относительная и абсолютная погрешности, а также выполнены два задания по вычислению относительной и абсолютной погрешностей функций.
Брук Тейлор (1685-1731) - английский математик.
1 Жозеф Луи де Лагранж (1736-1813) - французский математик, механик и астроном.
