
ПР2_Отчёт_ЗаболотниковМЕ_9373
.docx
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра информационных систем
отчет
по практической работе №2
по дисциплине «Теория информации, данные, знания»
Тема: Количество информации. Формула Хартли. Формула Шеннона
Студент(ка) гр. 9373 |
|
Заболотников М.Е. |
Преподаватель |
|
Писарев И. А. |
Санкт-Петербург
2020
Цель работы
Сформулировать ответы на вопросы с указанием источников информации.
Вопросы по теме 1:
1. Формула измерения количества информации Р. Хартли
2. Понятие информационной энтропии. Единицы измерения энтропии
3. Развитие теории информации в работах Клода Шеннона. Формула Шеннона
4. Решить две задачи:
4.1 Привести пример вычисления формулы Хартли для определения числа вопросов в задаче угадывания задуманного числа из заданного интервала (например, 1-32, 1-100). Представить вопросы и ответы для данного примера.
4.2 Выбрать любое предложение из текста на русском языке, содержащее не менее 20 букв русского алфавита. Рассчитать количество энтропии, содержащееся в предложении текста по формулам Хартли и Шеннона. Для формулы Шеннона воспользуйтесь частотами встречаемости букв в Национальном Корпусе Русского языка, приведенными в Приложении. Провести сравнение полученных значений.
Выполнение работы
Количество информации
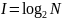
Информационная энтропия – это мера неопределённости состояния некоторой случайной величины (физической системы) с конечным или счётным числом состояний. Информационная энтропия, как и количество информации, измеряется в битах. Один бит – это энтропия системы с двумя равновероятными состояниями.
Клод Шеннон занимался вопросами передачи информации и ставил перед собой целью «определить систему кодирования, позволяющую оптимизировать скорость и достоверность передачи информации». В своих работах 1948-1949 гг. американский инженер определил понятие количества информации через понятие энтропии – меры разупорядоченности системы. За единицу измерения энтропии Шеннон принял так называемый бит.
Клод, используя подход Хартли, обратил внимание на то, что при передачи словесных сообщений частота использования различных букв не одинакова. Одни букв используются чаще, другие – реже.
Пусть у нас есть
алфавит
 ,
состоящий из m
символов. Обозначим через
,
состоящий из m
символов. Обозначим через
 вероятность
(частоту) появления i-ого символа в любой
позиции
вероятность
(частоту) появления i-ого символа в любой
позиции
передаваемого сообщения, состоящего из n символов. Один i-ый символ
алфавита несёт количество информации равное
логарифмом стоит «минус» потому, что количество информации величина
неотрицательная,
а
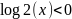 при
при
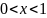 .
.
На месте каждого символа в сообщении может стоять любой символ
Алфавита ; количество информации, приходящееся на один символ
сообщения, равно среднему значению информации по всем символам
алфавита :
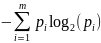
Общее количество информации, содержащееся в сообщении из n символов
равно:

Это и есть формула Шеннона для количества информации при разновероятных событиях.
1. Пусть у нас есть множество натуральных чисел
 .
Загадано какое-то число из этого
множества, пусть это будет 49. За какое
минимальное количество вопросов можно
гарантированно верно угадать задуманное
число?
.
Загадано какое-то число из этого
множества, пусть это будет 49. За какое
минимальное количество вопросов можно
гарантированно верно угадать задуманное
число?
Решение. Чтобы
решить данную задачу, необходимо задавать
такие вопросы, которые требуют ответа
«да» или «нет». По формуле Хартли
количество информации, которое надо
получить, равно
 бит. Это означает, что мы должны управиться
за шесть вопросов. Итак, поехали:
бит. Это означает, что мы должны управиться
за шесть вопросов. Итак, поехали:
Делим наше множество на две части и спрашиваем: «Задуманное число находится в пределах от 1 до 32?». Число 49 не входит в это множество, поэтому ответ – нет.
Искать придётся в множестве чисел от 33 до 64. Делим его пополам. Вопрос: «Задуманное число принадлежит множеству
 ?»
Ответ – нет, не принадлежит. Значит,
число лежит в пределах от 49 до 64.
?»
Ответ – нет, не принадлежит. Значит,
число лежит в пределах от 49 до 64.Снова делим полученное множество пополам, задаём вопрос: «Задуманное число лежит в множестве
 ?»
Ответ – да, лежит.
?»
Ответ – да, лежит.
«Это число принадлежит множеству
 ?»
Да.
?»
Да.«Загаданное число принадлежит множеству
 ?»
Нет.
?»
Нет.«Загаданное число – 50?» Нет.
Ответ. Значит, задуманное число – 49. Ура! Ровно за шесть простых ходов-вопросов мы угадали задуманное число.
2. Имеется предложение: «Научившись измерять время, его длительность, мы до сих пор пытаемся понять его природу.» Рассчитать количество энтропии, содержащееся в этом предложении, по формулам Хартли и Шеннона.
Решение. По
формуле Хартли количество энтропии
вычисляется как
 ,
где
,
где
 – количество букв в предложении, а
– количество букв в предложении, а
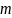 – количество символов в алфавите. Итак,
– количество символов в алфавите. Итак,
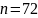 ,
а
,
а
 ,
значит, количество энтропии
,
значит, количество энтропии
 .
Значит, значение энтропии предложения
находится в пределах от 363 до 364 с точностью
до бита.
.
Значит, значение энтропии предложения
находится в пределах от 363 до 364 с точностью
до бита.
Если брать в расчёт формулу Шеннона, то количество энтропии предложения будет вычисляться как: .
Итак,
,
мы это уже знаем. Осталось вычислить
вот эту огромную сумму логарифмов. После
долгих вычислений выяснилось, что сумма
равна
 .
Далее
.
Далее
 .
Следовательно, по новым данным энтропия
предложения оценивается промежутком
от 308 до 309 с точностью до 1 бита.
.
Следовательно, по новым данным энтропия
предложения оценивается промежутком
от 308 до 309 с точностью до 1 бита.
Ответ:
 ,
по методу Хартли; и
,
по методу Хартли; и
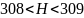 ,
по формуле К. Шеннона.
,
по формуле К. Шеннона.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
https://yadi.sk/i/g387TDYOrKwdUw
https://yadi.sk/i/7pJFBKLTDqpkPQ
https://yadi.sk/i/0dXA4T4Hhi93_Q
