_МИНИстерство науки и высшего образования РФ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра информационных систем

Курсовая работа

по дисциплине «Моделирование систем массового обслуживания»

Работа оценена на 84 %.

Комментарий преподавателя: Моделирование используется для подбора параметров, чтобы сделать систему лучше. У вас получился высокий процент отказа, но вы не делаете чётких рекомендаций через эксперимент. Как-то средне подошли к работе.

Студент гр. 93—		—
Преподаватель		Татарникова Т. М.

Санкт-Петербург

2022

Задание на курсовую работу

Студент —

Группа: 93—

Тема работы: Моделирование системы массового обслуживания

Исходные данные:

На комплектовочный конвейер сборочного цеха каждые 5 ± 1 мин поступают 5 изделий первого типа и каждые 20 ± 7 мин поступают 20 изделий второго типа. Конвейер состоит из секций, вмещающих по 10 изделий каждого типа. Комплектация начинается только при наличии деталей обоих типов в требуемом количестве и длится 10 мин. При нехватке деталей секция конвейера остаётся пустой.

Смоделировать работу конвейера сборочного цеха в течение 8 ч. Определить вероятность пропуска секции, средние и максимальные очереди по каждому типу изделий. Определить экономическую целесообразность перехода на секции по 20 изделий с временем комплектации 20 мин.

Содержание пояснительной записки:

«Введение», «Построение концептуальной модели», «Разработка имитационной модели», «Проведение экспериментов», «Анализ результатов».

Дата выдачи задания: 01.09.2022

Дата сдачи задания: 24.12.2022

Студент гр. 93—		—
Преподаватель		Татарникова Т. М.

Аннотация

В данной курсовой работе представлены концепции, используемые при разработке имитационных моделей: анализ задачи, формализация, выполнение экспериментов, анализ результатов. Результатом работы является созданная имитационная модель сборочного цеха.

Содержание

1. Построение концептуальной модели 5

2. Разработка имитационной модели 7

3. Проведение экспериментов 11

4. Анализ результатов 14

Перед организацией работы сборочного цеха могут возникнуть различные проблемы при нестабильности системы. Чтобы их избежать, необходимо спроектировать имитационную модель работы цеха и проанализировать стабильность полученных результатов.

1. Построение концептуальной модели

Составим структурную схему процесса функционирования системы.

Рисунок 1.1. Структурная схема функционирования модели.

Возникновение очередей возможно в секциях, когда происходит комплектация деталей, а также перед секциями, если секция полностью заполнена. Очередь формируется по правилу FIFO (первый пришёл — первый вышел). В работе будет оцениваться средняя и максимальная длины очереди по каждому из изделий.

Применение аналитического подхода к данной задачи невозможно или очень затруднительно без упрощения модели, поэтому в данной работе используется имитационный метод моделирования.

Построим Q-схему рассматриваемой модели.

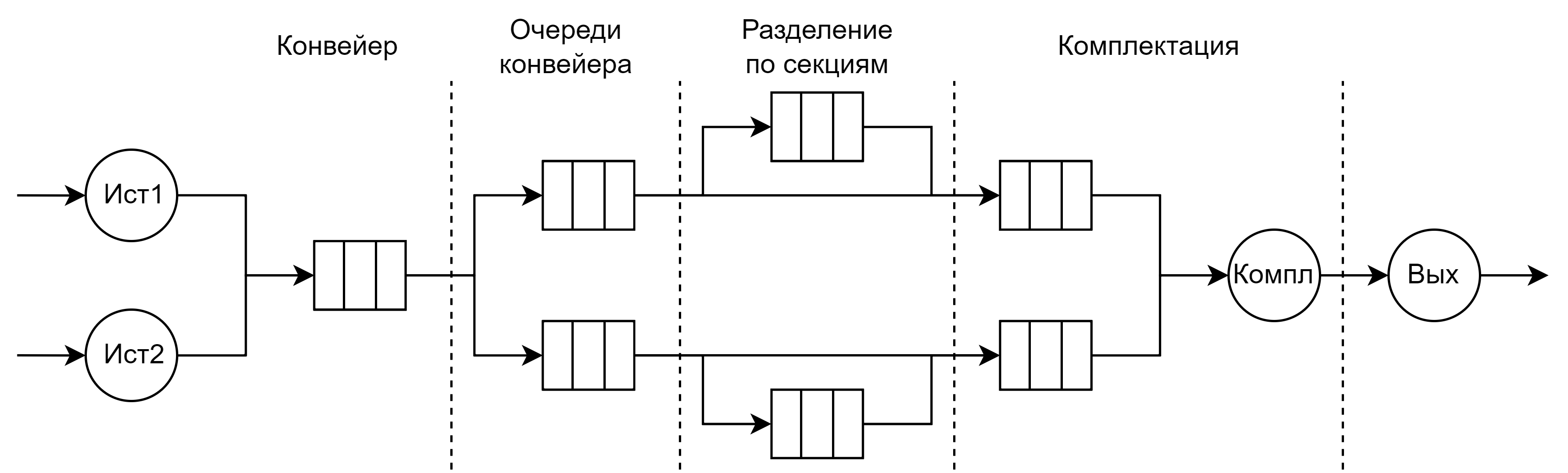
Рисунок 1.2. Q-схема системы.

Для того, чтобы организовать комплектацию, понадобятся два накопителя по 10 деталей, детали которых одновременно поступают на сборку. В случае, если накопители заполнены, используются секции конвейера, которые также вмещают по 10 деталей.

Детали поступают на конвейерную ленту, организованную в виде неограниченной очереди. Затем для подсчёта длины очереди каждого типа деталей конвейер разделяется на две очереди. После этого деталь помещается в соответствующей её типу накопитель комплектации или, если накопитель занят, отправляется в специальную секцию конвейера, вместимость каждой из которых составляет 10 деталей.

На вход системы поступает два потока деталей по времени с равномерным распределением (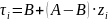 ). Время сборки — константное, равное 10 минутам.

2. Разработка имитационной модели

Для разработки имитационной модели используется программное обеспечение AnyLogic (разработчик: The AnyLogic Company).

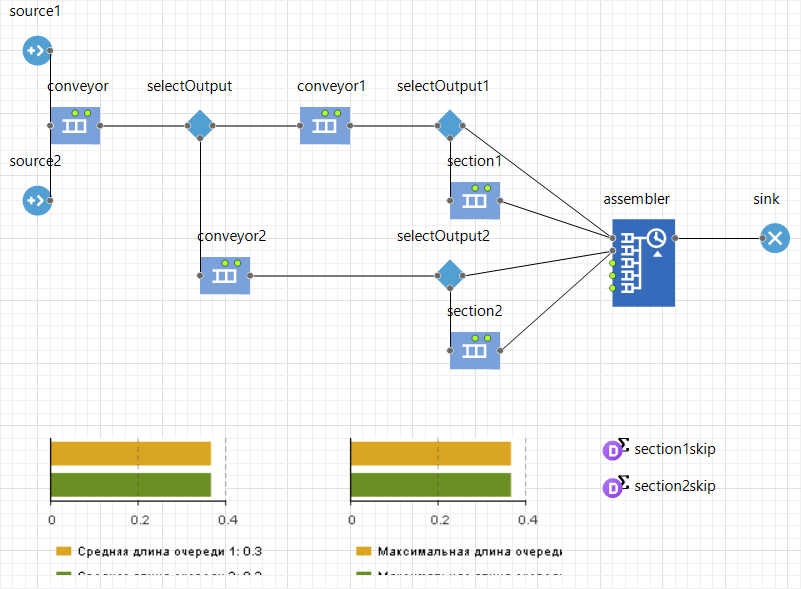
Рисунок 2.1. Схема имитационной модели в среде AnyLogic.

В качестве двух накопителей и сборщика с задержкой выступил объект «assembler».

«source1» и «source2» генерируют агенты с первым и вторым типами соответственно за случайное равномерно-распределённое время.

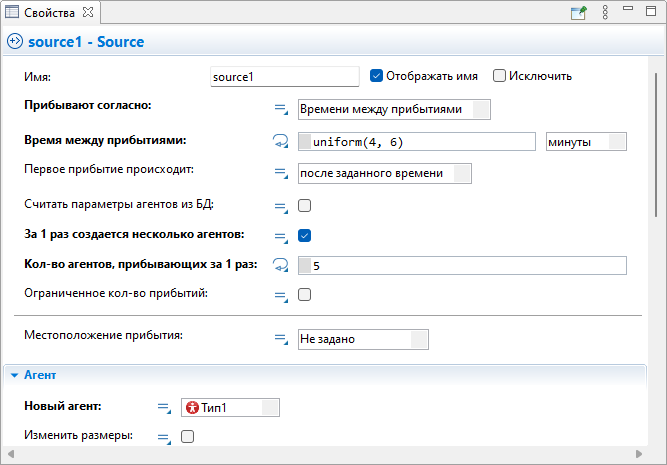
Рисунок 2.2. Свойства объекта «source1».

В отличие от «source1» объект «source2» генерирует 20 агентов «Тип2» со временем между прибытием, равным uniform(13, 27) мин.

Оба источника отправляют своих агентов в бесконечную очередь «conveyor».

Затем агенты попадают в объект «selectOutput», который распределяет агентов в зависимости от их типа по двум разным очередям. Это делается с помощью условия agent instanceof Тип1.

Эти очереди нужны для подсчёта длины очереди на конвейере для каждой из типа деталей. Для этого созданы две столбиковые диаграммы. В одной из них считается средняя длина очереди с помощью conveyor1.statsSize.mean() и conveyor2.statsSize.mean() соответственно для первого и второго конвейеров. Во второй — максимальная длина с помощью conveyor1.statsSize.max() и conveyor2.statsSize.max().

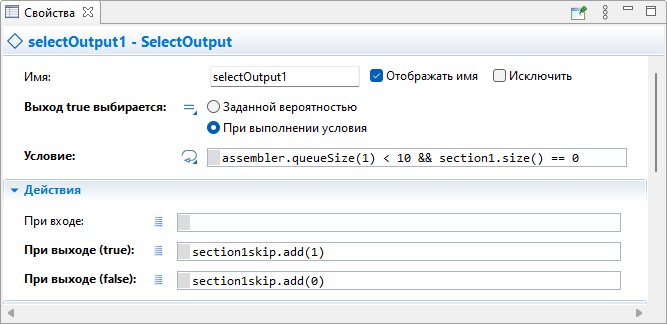
Рисунок 2.3. Свойства объекта «selectOutput1».

После конвейерных очередей агенты попадают в объект «selectOutput1» или «selectOutput2». Эти объекты определяют заполненность объекта «assembler» соответствующим типом детали. Если «assembler» свободен, то деталь отправляется в него, иначе она поступает в очередь «section1» или «section2» с вместимостью 10 каждая и ожидает там. Условия, которые реализуют вышеописанное выглядят следующим образом:

1. assembler.queueSize(1) < 10 && section1.size() == 0

2. assembler.queueSize(2) < 10 && section2.size() == 0

Для нахождения вероятности пропуска секций используются объекты сбора статистики «section1skip» и «section2skip», которые вычисляют основную статистическую информацию для последовательности измеренных значений. При отправке детали в секцию в статистическую информацию добавляется 0 (section1skip.add(0)), при отправке в сборщик — 1 (section1skip.add(1)). Затем в режиме имитации можно будет увидеть среднее значение добавленных данных.

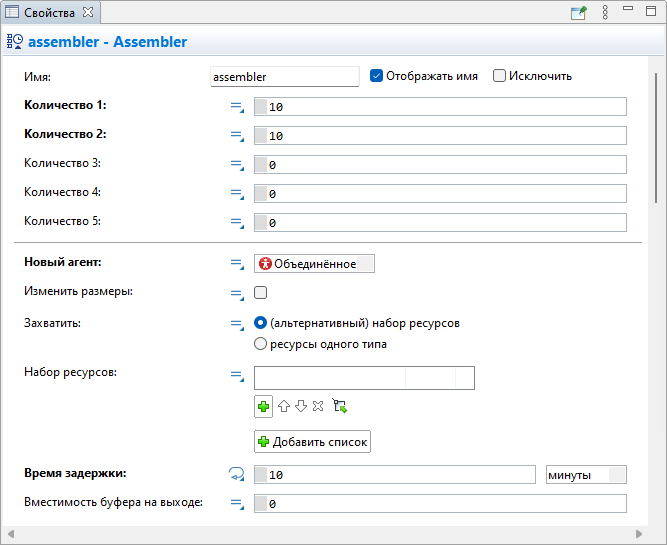
Рисунок 2.4. Свойства объекта «assembler».

Объект сборщика требует для сборки одной объединённой детали по 10 деталей каждого типа, и сборка занимает 10 минут. После комплектации моделируемый процесс заканчивается.

3. Проведение экспериментов

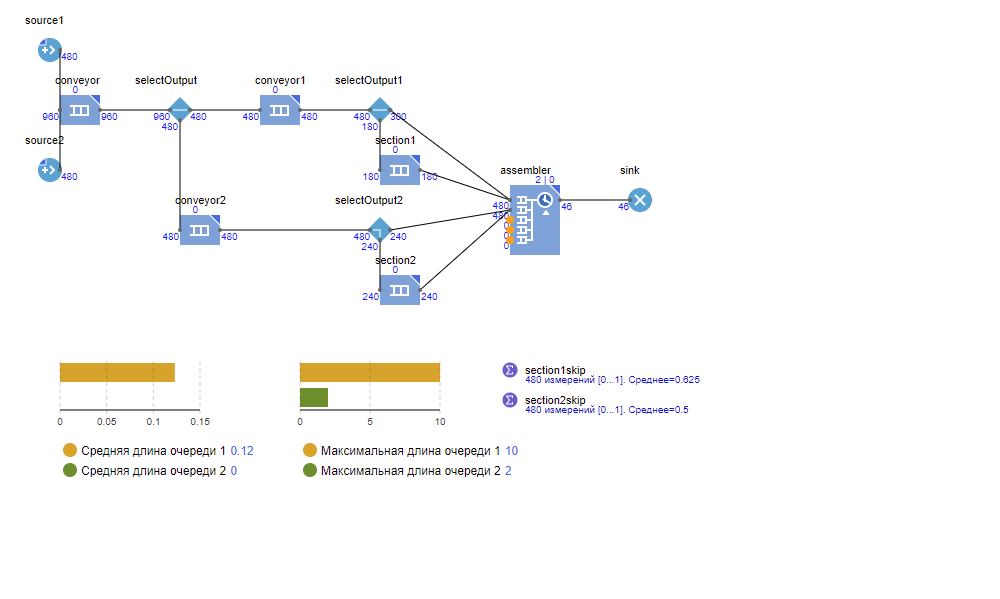
Рисунок 3.1. Состояние модели после симуляции в течение 8 часов.

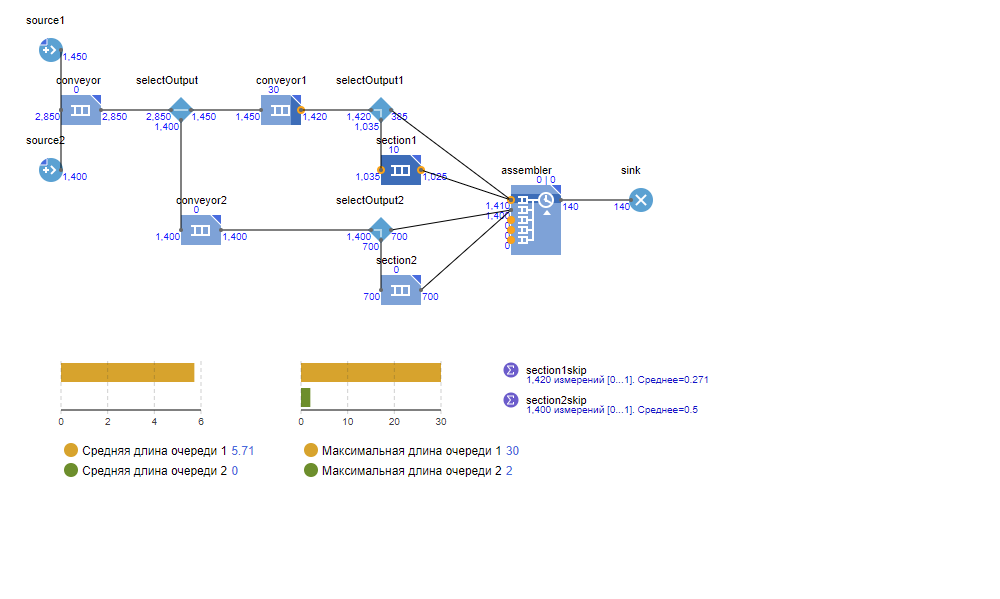
Рисунок 3.2. Состояние модели после симуляции в течение 1 дня.

Перейдём на секции по 20 изделий с временем комплектации 20 минут.

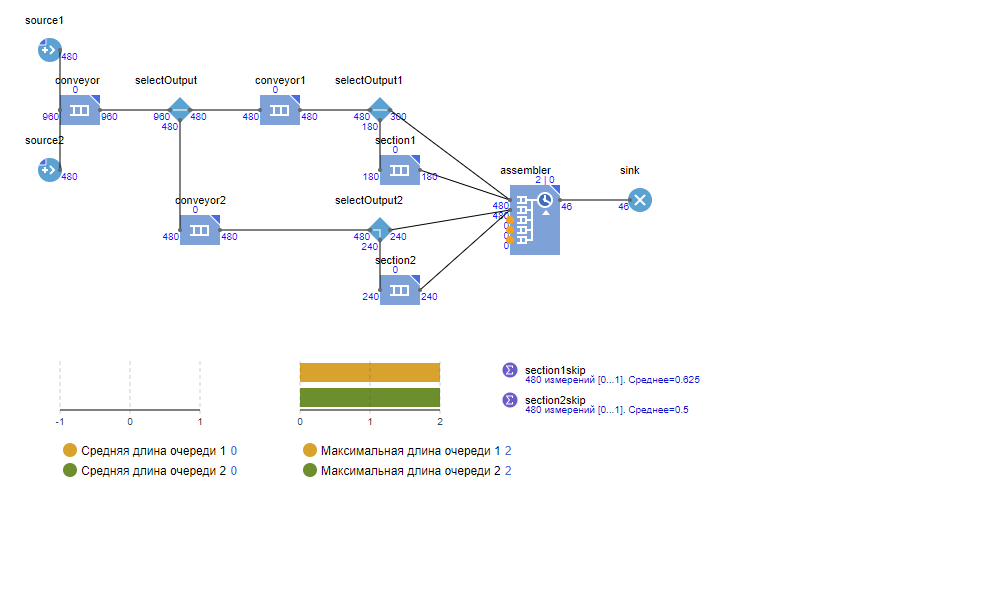
Рисунок 3.3. Состояние изменённой модели после симуляции в течение 8 часов.

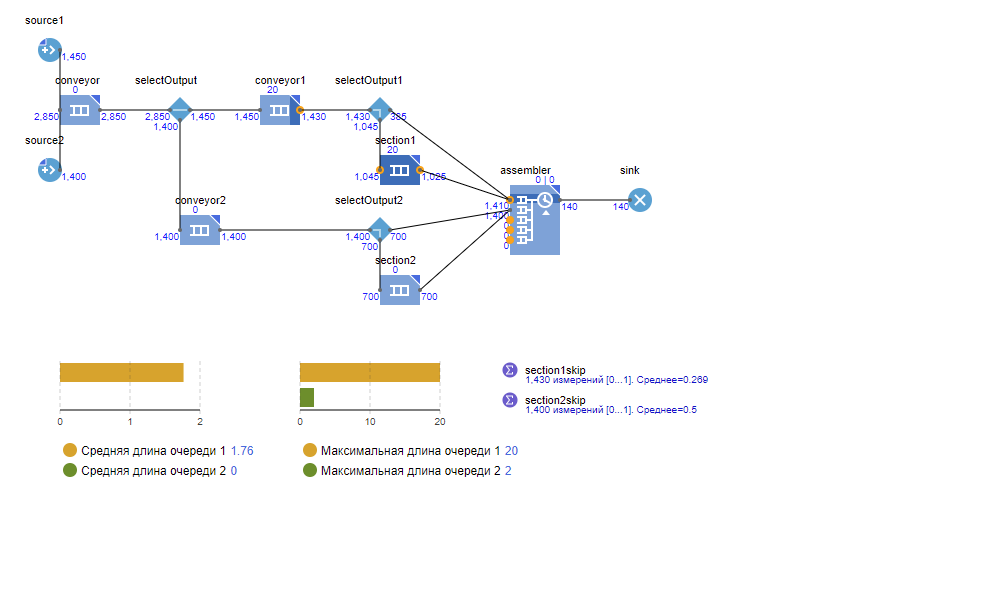
Рисунок 3.4. Состояние изменённой модели после симуляции в течение 1 дня.

Изменив частоту прихода деталей второго типа с 20 деталей за 20 ± 7 мин до 10 деталей за 10 ± 3,5 мин, получим стабильно работающую систему в течение 24 часов.

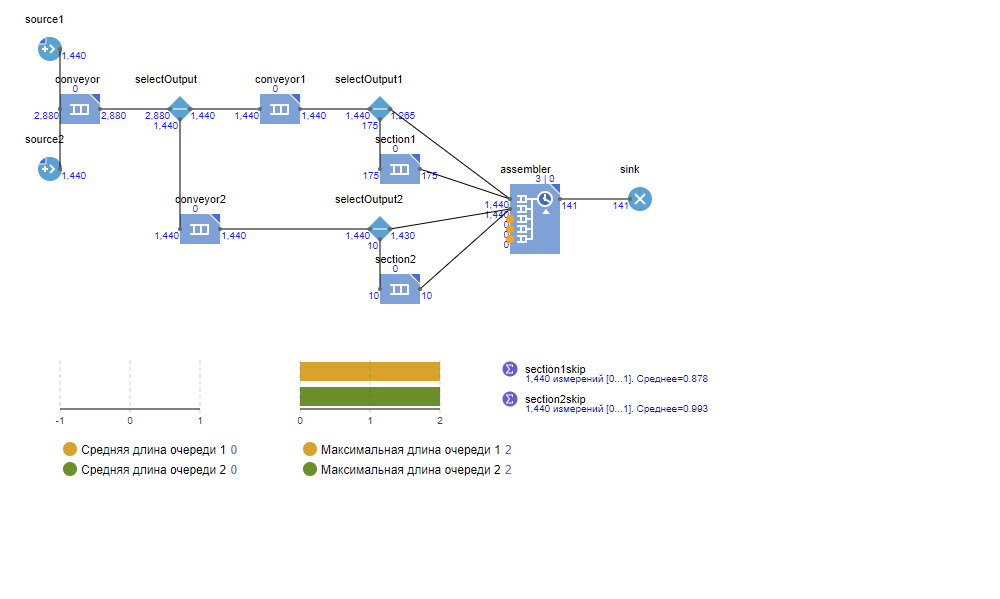
Рисунок 3.5. Состояние модели после симуляции в течение 1 дня после изменений в частоте прихода деталей второго типа.

4. Анализ результатов

Результаты системы после 8 часов работы:

• вероятность пропуска секции:

  • для первого типа — 0,625,

  • для второго типа — 0,5;

• средняя очередь секции:

  • для первого типа — 0,12,

  • для второго типа — 0;

• максимальная очередь секции:

  • для первого типа — 10,

  • для второго типа — 2.

После запуска модели на 24 часа длина очереди для деталей первого типа со временем возрастает (средняя: с 0,12 до 5,71; максимальная: с 10 до 30), и, соответственно, вероятность пропуска секции снижается (с 0,625 до 0,271). Изменение в характеристиках говорит о нестабильности системы.

Оценим целесообразность перехода на секции по 20 изделий с временем комплектации 20 минут. После изменения в модели очереди на конвейере пропали. Впрочем, система осталась нестабильной: в течение 24 часов очередь всё же появилась. Изменение времени сборки с 10 до 20 минут, в целом, ни на что не повлияло.

Рекомендации по реализации

В системе может образоваться очередь из деталей первого типа, поэтому при её реализации стоит избегать длительных запусков и увеличить частоту производства деталей второго типа в два раза.