
ИДЗ 3
.docx
|
Студент: Группа: Вариант: Дата: |
— 93— 7 12 июня 2021 г. |
Теория вероятностей и математическая статистика Индивидуальное домашнее задание №3
Случайная
величина
 имеет равномерное распределение в
области
имеет равномерное распределение в
области


Задача 1. Найти
 ,
функции и плотности распределения
компонент. Будут ли компоненты
независимыми?
,
функции и плотности распределения
компонент. Будут ли компоненты
независимыми?

Решение. Изобразим заданную область и найдём её площадь.

Тогда функция плотности такова:

Найдём плотности распределения компонент по следующим формулам:
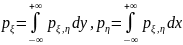
Таким образом, в области
 :
:


Вне этой области интегралы, очевидно, равны 0.
Поэтому:

Определим, независимые ли компоненты.

В точке
 выражение
выражение
 ,
когда же
,
когда же
 .
.
 ,
значит компоненты не являются независимыми.
,
значит компоненты не являются независимыми.
Ответ:

Задача
2. Найти распределения
случайных величин
 и
и
 ;
;
 ,
,
 ,
,
 ,
,
 .
.

Решение. Найдём распределение случайной величины .
Рассмотрим случай при
 (
( ):
):

В итоге:

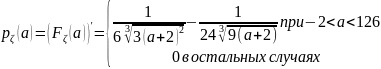
Вычислим и :




Найдём распределение случайной величины .
 при
при
 ;
;

Вычислим вероятности при остальных значениях по аналогии и заполним таблицу:
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
0,19 |
0,17 |
0,15 |
0,13 |
0,11 |
0,09 |
0,07 |
0,05 |
0,03 |
0,01 |
Найдём и :
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
0,19 |
0,17 |
0,15 |
0,13 |
0,11 |
0,09 |
0,07 |
0,05 |
0,03 |
0,01 |
|
0,95 |
1,02 |
1,05 |
1,04 |
0,99 |
0,9 |
0,77 |
0,6 |
0,39 |
0,14 |
|
4,75 |
6,12 |
7,35 |
8,32 |
8,91 |
9 |
8,47 |
7,2 |
5,07 |
1,96 |


Ответ:
-
5
6
7
8
9
10
11
12
13
14
0,19
0,17
0,15
0,13
0,11
0,09
0,07
0,05
0,03
0,01


Задача 3. Вычислить вектор
математических ожиданий и ковариационные
характеристики вектора
 .
.

Решение. Вычислим вектор математических ожиданий вектора .


Вычислим ковариационные характеристики вектора по следующей формуле:

Найдём величины
 и
и
 :
:



Ответ:
 .
.
Задача
4. Найти распределение
 ;
;
 ,
,
 .
.
Решение. Найдём распределение :

Рассмотрим три случая:
-



Тогда
 при
при
 .
.
Тогда
 при
при
 .
.
 При
При
 :
:
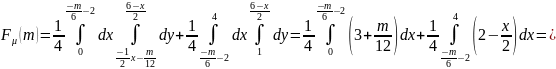

В итоге:


Найдём и :


Ответ:
 .
.



