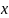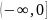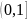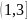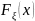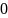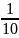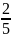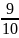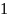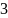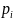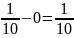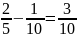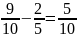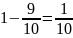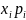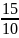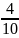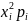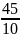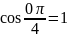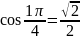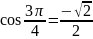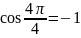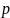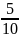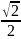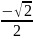ИДЗ 2
.docx
|
Студент: Группа: Вариант: Дата: |
— 93— 7 10 июня 2021 г. |
Теория вероятностей и математическая статистика Индивидуальное домашнее задание №2
Задача 1. Вероятность успеха в схеме Бернулли равна ½. Проводится 3000 испытаний. Написать точную формулу и вычислить приближённо вероятность того, что число успехов попадёт в интервал [1486, 1514].
Решение. Вероятность того, что в
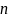 испытаниях успех наступит ровно
испытаниях успех наступит ровно
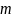 раз, можно вычислить по формуле Бернулли:
раз, можно вычислить по формуле Бернулли:
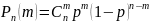
Чтобы число успехов попало в интервал
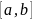 ,
нужно по теореме сложения вероятностей
вычислить выражение:
,
нужно по теореме сложения вероятностей
вычислить выражение:
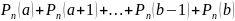
Тогда точная формула для вычисления «вероятности того, что число успехов попадёт в интервал [1486, 1514]» такая:
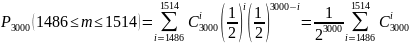
Для приближённого вычисления воспользуемся интегральной теоремой Лапласа:
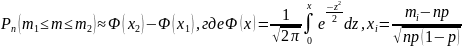
Вычислим
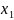 и
и
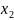 :
:
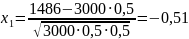
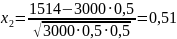
По таблице значений функции Лапласа
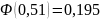 ;
;
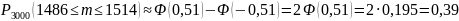
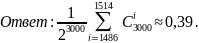
Задача
2. Дана функция распределения
случайной величины
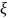 :
:
|
|
|
|
|
|
|
|
|
|
|
|
Вычислить
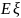 ,
,
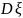 и распределение
и распределение
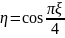 .
.
Решение. Найдём математическое ожидание и дисперсию .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
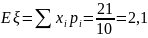
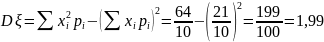
Составим закон распределения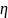 .
.
Ответ:
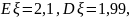
Задача 3. Дана плотность распределения
абсолютной непрерывной случайной
величины
: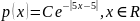 .
Вычислить
.
Вычислить
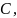 ,
и распределение
,
и распределение
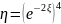 .
.
Решение. Найдём константу
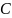 .
.
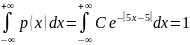
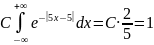
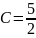
Получается, что
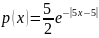 .
.
Найдём математическое ожидание и дисперсию .
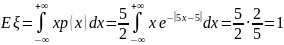
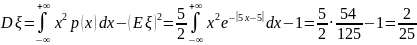
Вычислим распределение .
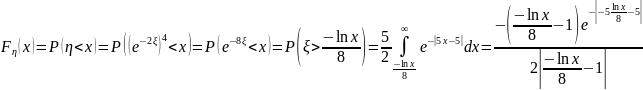
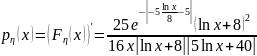
Ответ:
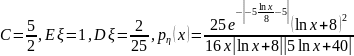 .
.