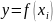ЛР7. 4.1. Аппроксимация функции по методу наименьших квадратов

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В. И. Ульянова (Ленина)

Кафедра ИС

отчет

по лабораторной работе №7

по дисциплине «Конструирование программ»

Тема: Аппроксимация функции по методу наименьших квадратов

Студент гр. 93—		—
Преподаватель		Копыльцов А. В.

Санкт-Петербург

2021

Цель работы.

Научится аппроксимировать функцию по методу наименьших квадратов.

Основные теоретические сведения.

Очень часто при анализе эмпирических данных необходимо найти явную функциональную зависимость между двумя величинам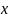и и 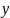, полученными в результате измерений. Поскольку опытные данные всегда содержат ошибки, то строить интерполяционный многочлен 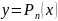не рационально, так как при интерполяции ошибки повторяются. Желательно по возможности сгладить и минимизировать ошибки наблюдений. Этот результат достигается построением многочлена наилучшего среднего квадратического приближения по методу наименьших квадратов.

Любая линейная функция может быть записана уравнением Аппроксимация заключается в отыскании коэффициентов a и b уравнения таких, чтобы все экспериментальные точки лежали наиболее близко к аппроксимирующей прямой.

С этой целью чаще всего используется метод наименьших квадратов (МНК), суть которого заключается в следующем: сумма квадратов отклонений значения точки от аппроксимирующей точки принимает минимальное значение: 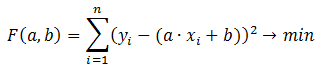Решение поставленной задачи сводится к нахождению экстремума указанной функции двух переменных. С этой целью находим частные производные функции по коэффициентам a и b и приравниваем их к нулю. 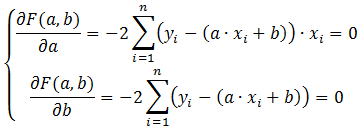Решаем полученную систему уравнений

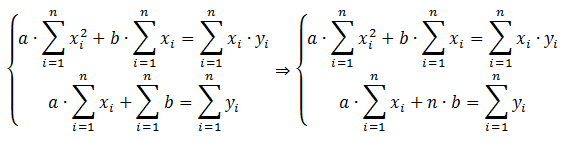
Определяем значения коэффициентов

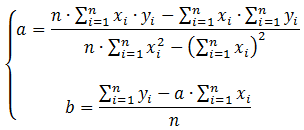
Для вычисления коэффициентов необходимо найти следующие составляющие:

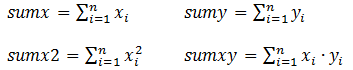
Тогда значения коэффициентов будут определены как

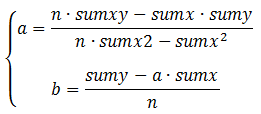
Экспериментальные результаты.

Задание № 1.

По методу наименьших квадратов аппроксимировать таблично заданную функцию .

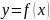0.1	12.28
0.2	12.53
0.3	12.50
0.4	12.53
0.5	12.75
0.6	12.85
0.7	12.77
0.8	12.76
0.9	12.73
1.0	12.85
1.1	12.51
1.2	12.34
1.3	12.22
1.4	11.84
1.5	11.67
1.6	11.27
1.7	11.06
1.8	10.73
1.9	10.35
2.0	10.09

Обработка результатов

Задание 1

y = -1.22x + 13.31

Выводы.

Были получены навыки аппроксимирования таблично заданной функции. Аппроксимация сгладила экспериментальные погрешности.

Приложение 1. Код программы

package j.softwareconstruction.lab4; public class Main { public static void main(String[] args) { task1(); } private static void task1() { System.out.println("Задание 1"); double[] x = {0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2.0}; double[] y = {12.28, 12.53, 12.50, 12.53, 12.75, 12.85, 12.77, 12.76, 12.73, 12.85, 12.51, 12.34, 12.22, 11.84, 11.67, 11.27, 11.06, 10.73, 10.35, 10.09}; double Sx = 0, Sx2 = 0, Sy = 0, Sxy = 0, Sx2y = 0; for (int i = 0; i < x.length; i++) { Sx += x[i]; Sx2 += x[i] * x[i]; Sy += y[i]; Sxy += x[i] * y[i]; Sx2y += x[i] * x[i] * y[i]; } final int n = x.length; double a = (n * Sxy - Sx * Sy) / (n * Sx2 - Sx * Sx); double b = (Sy - a * Sx) / n; String aFormat = String.format("%.2f", a); String bFormat = String.format("%.2f", Math.abs(b)); System.out.println("\ty = " + aFormat + "x " + (b < 0 ? "- " : "+ ") + bFormat); } }