5. Эффективное кодирование. Код Шеннона-Фано

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра информационных систем

отчЁт

по практической работе №5

по дисциплине «Теория информации, данные, знания»

Тема: Эффективное кодирование. Код Шеннона-Фано.

Студент гр. 93—		—
Преподаватель		Писарев И. А.

Санкт-Петербург

2020

Цель работы

Сформулировать ответы на вопросы с указанием источников информации.

Вопросы по теме:

1. Дайте определение методов эффективного (оптимального) кодирования.

2. Основная теорема Шеннона о эффективном кодировании.

3. Опишите метод Шеннона-Фано.

Решить задачи:

1. Закодировать сообщение методом Шенона-Фано.

Сообщение	a	b	c	d	e	f	g
Вероятность	0,4	0,2	0,2	0,05	0,05	0,05	0,05

2. Алфавит содержит 7 букв, которые встречаются с вероятностями 0,4; 0,2; 0,1; 0,1; 0,1; 0,05; 0,05. Осуществить кодирование по методу Шенона-Фано.

Выполнение работы

Вопрос 1.

Методы, сжимающие информацию, то есть уменьшающие количество бит, необходимых для хранения или передачи заданной информации, что даёт возможность и оперативнее передавать и экономней хранить сообщения.

Вопрос 2.

Доказано, что среднее количество бит, приходящихся на одно кодируемое значение д. с. в., не может быть меньшим, чем энтропия этой д. с. в., т. е. 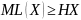для любой д. с. в. 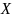и любого её кода. Кроме того, доказано утверждение, о том что существует такое кодирование, что

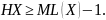
Рассмотрим д. с. в. 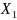и 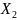, независимые и одинаково распределённые. 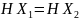и .

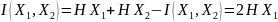Вместо и можно говорить о двумерной д. с. в. 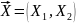. Аналогичным образом для 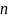-мерной д. с. в. 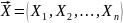можно получить, что .

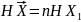Пусть 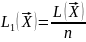, где , т. е. 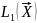— это количество бит кода на единицу сообщения 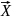. Тогда 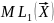— это средние количество бит кода на единицу сообщения при передаче бесконечного множества сообщений . Из 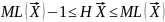для кода Шеннона-Фэно для следует 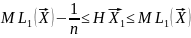для этого же кода.

(2, С. 31—32)

Вопрос 3.

Кодируемые знаки выписывают в таблицу в порядке убывания их вероятностей в сообщениях. Затем их разделяют на две группы так, чтобы значения сумм вероятностей в каждой группе были близкими. Все знаки одной из групп в соответствующем разряде кодируются, например, единицей, тогда знаки второй группы кодируются нулём. Каждую полученную в процессе деления группу подвергают вышеописанной операции до тех пор, пока в результате очередного деления в каждой группе не останется по одному знаку. (1, С. 57)

Задача 1.

Сообщение	Вероятность	Процесс кодирования				Код
a	0,4	0 (0,6)	0			00
b	0,2		1			01
c	0,2	1 (0,4)	0			10
d	0,05		1 (0,2)	0 (0,1)	0		1100
e	0,05				1		1101
f	0,05			1 (0,1)	0		1110
g	0,05				1		1111

Задача 2.

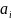
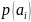
		Процесс кодирования				Код
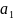
	0,4	0 (0,6)	0			00
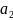
	0,2		1			01
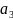
	0,1	1 (0,4)	0 (0,2)	0			100
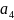
	0,1			1			101
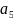
	0,1		1 (0,3)	0			110
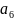
	0,05			1 (0,1)	0		1110
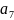
	0,05				1		1111

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Гошин Е.В. Теория информации и кодирования. Самара: Самарский университет. 2018. 124 с.

2. Лидовский В.В. Основы теории информации и криптографии. Учебное пособие. Изд. 2-е, испр. М. : Интернет-университет информационных технологий, 2016. 142 с.