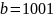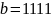4. Основы теории кодирования. Код Хемминга

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра информационных систем

отчЁт

по практической работе №4

по дисциплине «Теория информации, данные, знания»

Тема: Основы теории кодирования. Код Хемминга.

Студент гр. 93—		—
Преподаватель		Писарев И. А.

Санкт-Петербург

2020

Цель работы

Сформулировать ответы на вопросы с указанием источников информации.

Вопросы по теме:

1. Сформулируйте задачу надёжной передачи сообщений.

2. Объясните, почему кодирование с контрольной суммой позволяет обнаружить в процессе передачи только нечётное число ошибок

3. Дайте определение расстояния Хэмминга между двоичными словами.

4. Какова связь обнаруживающей способности кода с минимальным расстоянием Хэмминга?

Решить задачу:

Для слов длины 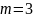в алфавите 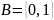используются кодовые слова длины 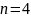( 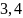– коды). Порождающая матрица 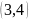имеет вид: 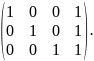Какую по кратности ошибку может обнаружить этот код?

1. Определить кодовое слово 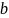для слова исходного сообщения .

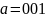2. Какое кодовое слово соответствует слову исходного сообщения

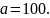
3. Какое кодовое слово соответствует слову исходного сообщения

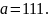
Выполнение работы

Вопрос 1.

Постановка задачи надёжной передачи сообщений состоит в следующем. Пусть по каналу связи требуется передавать слова в некотором алфавите 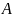. На вход канала подаётся слово 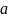, а на выходе принимается искажённое слово 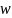. Требуется по слову восстановить слово . (1, С. 118)

Вопрос 2.

Ясно, что такое кодирование позволяет обнаружить в процессе передачи только нечётное число ошибок. Пусть надо передать слово 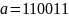, , 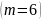тогда 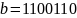(контрольная сумма 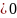). Если после передачи вместо кода будет получено слово 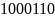, то будет обнаружено наличие ошибки. Если будет получено, например, слово 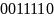, то ошибка обнаружена не будет. (1, С. 119)

Вопрос 3.

Пусть 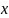и 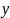– двоичные слова длины 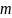в алфавите 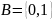. Введём расстояние Хемминга между и следующим образом: 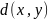равно числу несовпадений в соответствующих позициях слов и . (1, С. 120–121)

Кодовое расстояние выражается числом символов, в которых последовательности отличаются друг от друга. (2, С. 74)

Степень различия любых двух кодовых комбинаций характеризуется расстоянием между ними (по Хэммингу), или просто кодовым расстоянием. Оно выражается числом символов, в которых комбинации отличаются одна от другой, и обозначается через . (3, С. 11)

Вопрос 4.

Пусть при передаче кодовых слов происходит не более k ошибок. Для того чтобы код являлся обнаруживающим, необходимо и достаточно чтобы наименьшее расстояние между кодовыми словами удовлетворяло неравенству: 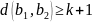(1, С. 121)

В общем случае при необходимости обнаружения ошибки кратности до 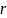включительно, минимальное кодовое расстояние должно удовлетворять условию 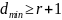. (2, С. 74)

В общем случае при необходимости обнаруживать ошибки кратности r минимальное хэммингово расстояние между разрешёнными кодовыми комбинациями должно быть по крайней мере на единицу больше , т. е, . (3, С. 12)

Задача.

Код может обнаружить ошибку по кратности 2 (нечётное число ошибок).

1. 

2. 

3. 

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Луковкин С. Б. Теоретические основы информатики: учебное пособие. Мурманск: Изд-во МГТУ. 2008. 125 с.

2. Гошин Е.В. Теория информации и кодирования. Самара: Самарский университет. 2018. 124 с.

3. Горбоконенко В.Д., Шикина В.Е. Кодирование информации. Методические указания. Ульяновск: УлГТУ. 2006. 56 с