
2. Количество информации. Формула Хартли. Формула Шеннона
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра информационных систем
отчЁт
по практической работе №2
по дисциплине «Теория информации, данные, знания»
Тема: Количество информации. Формула Хартли. Формула Шеннона.
Студент гр. 9300 |
|
ФИО |
Преподаватель |
|
Писарев И. А. |
Санкт-Петербург
2020
Цель работы
Сформулировать ответы на вопросы с указанием источников информации.
Вопросы по теме:
Формула измерения количества информации Р. Хартли.
Понятие информационной энтропии. Единицы измерения энтропии.
Развитие теории информации в работах Клода Шеннона. Формула Шеннона.
Решить задачи:
Привести пример вычисления формулы Хартли для определения числа вопросов в задаче угадывания задуманного числа из заданного интервала (например, 1-32, 1-100). Представить вопросы и ответы для данного примера.
Выбрать любое предложение из текста на русском языке, содержащее не менее 20 букв русского алфавита. Рассчитать количество энтропии, содержащееся в предложении текста по формулам Хартли и Шеннона. Для формулы Шеннона воспользуйтесь частотами встречаемости букв в Национальном Корпусе Русского языка, приведёнными в Приложении. Провести сравнение полученных значений.
Выполнение работы
Вопрос 1.
Пусть передаётся
последовательность из
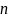 символов
символов
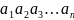 ,
каждый из которых принадлежит алфавиту
,
каждый из которых принадлежит алфавиту
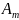 ,
содержащему
,
содержащему
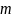 символов. Чему равно число
символов. Чему равно число
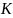 различных вариантов таких последовательностей?
Если передаётся один символ, то
различных вариантов таких последовательностей?
Если передаётся один символ, то
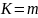 ;
если передаётся последовательность из
2-х символов, то
;
если передаётся последовательность из
2-х символов, то
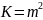 ;
в общем случае для последовательности
из
символов получим:
;
в общем случае для последовательности
из
символов получим:
 .
.
Количество
информации, содержащееся в такой
последовательности, Хартли предложил
вычислять как логарифм числа
по основанию
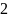 :
:
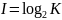 .
.
То есть, количество
информации, содержащееся в последовательности
из
символов из алфавита
,
в соответствии с формулой Хартли равно
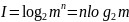 .
.
Замечание. Хартли предполагал, что все символы алфавита могут с равной вероятностью встретиться в любом месте сообщения. (3, С. 23)
При равномерном
распределении количество информации
задаётся формулой Хартли:
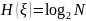 .
(2, С. 17)
.
(2, С. 17)
К количеству информации (неопределённости до опыта) можно предъявить три интуитивных требования.
Количество
получаемой информации больше в том
опыте, у которого большее число возможных
исходов. Обозначая количество информации
буквой
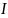 ,
а число возможных исходов
,
первый постулат запишем в виде:
,
а число возможных исходов
,
первый постулат запишем в виде:
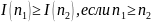 .
.
Опыт с единственным
исходом несёт количество информации,
равное нулю, т.е.
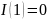 .
.
Количество
информации от двух независимых опытов
равно сумме количества информации от
каждого из них:
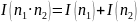 .
.
Очевидно, единственной
функцией аргумента n, удовлетворяющей
трём поставленным условиям, является
логарифмическая. Итак, количество
информации от опыта с N исходами при
условии, что после опыта неопределённость
отсутствует:
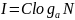 .
.
Выбор постоянной
С и основания логарифмов здесь
несущественен, так как определяет только
масштаб на единицу неопределённости.
Поэтому положим
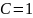 ,
,
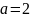 .
Тогда
.
Тогда
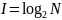 .
.
Указанная мера была предложена Р. Хартли в 1928г. для количественной оценки способности системы хранить или передавать информацию. (1, С. 39)
Вопрос 2.
Информационная энтропия – это мера неопределённости состояния некоторой случайной величины (физической системы) с конечным или счётным числом состояний.
Если все значения
случайной величины
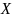 равновероятны, то энтропия величины
равна:
равновероятны, то энтропия величины
равна:
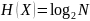 .
.
Энтропия и количество информации измеряются в одних и тех же единицах – в битах. 1 бит – это энтропия системы с двумя равновероятными состояниями. (3, С. 25)
Полученную величину
К. Шеннон назвал энтропией и обозначил
буквой
 ,
бит:
,
бит:

Энтропия представляет собой логарифмическую меру беспорядочности состояния источника сообщений и характеризует степень неопределённости состояния этого источника. (1, С. 41)
Вопрос 3.
К. Шеннон изучал вопросы передачи информации в телеграфии, телефонии или радиовещании в виде сигналов электромагнитных колебаний. Одна из задач, которую ставил перед собой К. Шеннон, заключалась в том, чтобы определить систему кодирования, позволяющую оптимизировать скорость и достоверность передачи информации. Так как в годы войны он служил в шифровальном отделе, где занимался разработкой криптографических систем, то это позже помогло ему открыть методы кодирования с коррекцией ошибок. В своих работах 1948-1949 годов К. Шеннон определил количество информации через энтропию - величину, известную в термодинамике и статистической физике как мера разупорядоченности системы, а за единицу количества информации принял то, что впоследствии назвали битом. (3, С. 30)
К. Шеннон, используя подход Р. Хартли, обратил внимание на то, что при передаче словесных сообщений частота использования различных букв алфавита не одинакова: некоторые буквы используются очень часто, другие – редко. (3, С. 31)
Общее количество
информации, содержащееся в сообщении
из n символов равно:
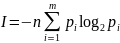 .
(3, С. 32)
.
(3, С. 32)
В общем случае
количество энтропии
произвольной системы
(случайной величины), которая может
находиться в
различных состояниях
 c вероятностями
c вероятностями
 ,
вычисленное по формуле Шеннона, равно
,
вычисленное по формуле Шеннона, равно
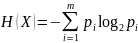 .
(3, С. 32–33)
.
(3, С. 32–33)
Количество
информации
 при наблюдении случайной величины
при наблюдении случайной величины
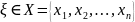 с распределением вероятностей
с распределением вероятностей
 задаётся формулой Шеннона:
задаётся формулой Шеннона:
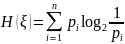 .
(2, С. 17)
.
(2, С. 17)
Задача 1.
Угадывание числа в диапазоне от 1 до 100.
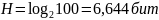
Значит, нужно задать 6–7 вопросов.
Загаданное число удовлетворяет условию
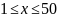 ?
Да.
?
Да.Загаданное число удовлетворяет условию
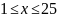 ?
Нет.
?
Нет.Загаданное число удовлетворяет условию
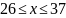 ?
Да.
?
Да.Загаданное число удовлетворяет условию
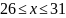 ?
Нет.
?
Нет.Загаданное число удовлетворяет условию
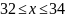 ?
Нет.
?
Нет.Загаданное число удовлетворяет условию
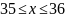 ?
Да.
?
Да.Загаданное число
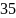 ?
Нет.
?
Нет.
Загаданное число — 36.
Задача 2.
Количество энтропии в предложении «Рассчитать количество энтропии, содержащееся в предложении текста по формулам Хартли и Шеннона».
По формуле Хартли:
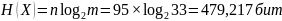
По формуле Шеннона:
 =
=
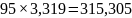 бит
бит
Как и предполагалось, количество энтропии по формуле Шеннона оказалось меньше.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Сорока Н.И., Кривинченко Г.А. Теория передачи информации. Минск: БГУИР, 2005. 301 с.
Зверева Е.Н., Лебедько Е.Г. Сборник примеров и задач по основам теории информации и кодирования сообщений. СПб: НИУ ИТМО, 2014. 76 с.
Луковкин С.Б. Теоретические основы информатики: учебное пособие. Мурманск: Изд-во МГТУ. 2008. 125 с.
