
лекции / KodRSLekciya7
.pdfДОПОЛНЕНИЕ К ЛЕКЦИИ №6 (СЛАЙД 11)

Получена система уравнений (с), из которой следуют 4 отдельных уравнений (d)
(d)

ПРИМЕР. Код БЧХ: n=15, t=3, GF(24), поле образовано по примитивному многочлену
P(x) 1 x x4 , корни : , 2 , 4 , 8 .
Корни порождающего многочлена G(x) : , 2 , 3 , 4 , 5 , 6 .
G(x) m1 (x)m3 (x)m5 (x).
Принятая комбинация:
h(x) h h x h x |
2 |
h x |
3 |
|
||
|
|
|||||
0 |
1 |
2 |
|
3 |
|
|
Многочлен локаторов ошибок:
... h |
14 |
x x |
2 |
x |
3 |
x |
5 |
x |
6 |
x |
8 |
12 |
x |
|
|
|
|
|
x . |
||||||
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
(z) (1 zi z) 1 1z 2 z2 3 z3.
i1
ЗАДАНИЕ: декодировать комбинацию по алгоритму Питерсона (ПГЦ), определить ошибочные позиции в комбинации и исправить ошибки при условии, что полученные декодером синдромы имеют вид:
S1= 13; S2= 11; S3= 12; S4= 7; S5=1; S6= 9;
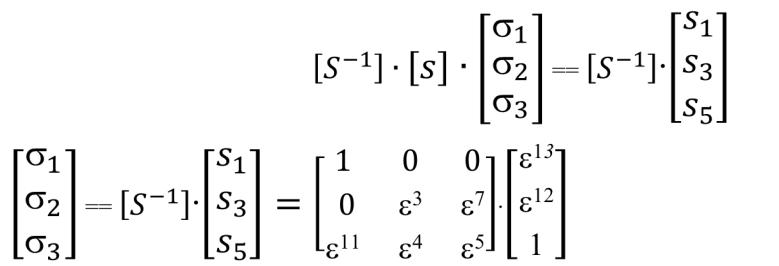
ИЛИ
Лекция 7 . Циклические коды Рида-Соломона (РС). |
7.1 |
|
Построение циклических кодов Рида-Соломона:
Исходные данные.
Образующий многочлен кода РС.
Образующая матрица систематического и несистематического кода РС. Проверочная матрица кода РС.
Декодирование комбинации кода РС.
Принципы обнаружения и исправления ошибок. Кратность исправляемых ошибок.
Многочлен локаторов ошибок.
Алгоритм исправления ошибок Питерсона-Горенстейна-Цирлера. Алгоритм Горнера вычисления синдромов.
Процедура Ченя определения ошибочных позиций кода. Алгоритм Евклида.
Алгоритм Берлекэмпа-Месси.

ЭЛЕМЕНТАМИ КОДА РИДА-СОЛОМОНА (недвоичного кода БЧХ) ЯВЛЯЮТСЯ ЭЛЕМЕНТЫ РАСШИРЕННОГО ПОЛЯ GF(2m)
Выберем в качестве порождающего поле GF(24) неприводимый по модулю 2 примитивный многочлен четвертой степени Р(х) = 1+ х + x4. Пусть является корнем данного многочлена, тогда он будет первообразным элементом поля GF(24). Все 15 ненулевых элементов поля будут
следующими (все степени приводятся по mod Р( )):
Таблица 2.1
В правой колонке таблицы элементы поля i
= a0 + a1 1+ a2 2+ a3 3
представлены в векторной форме записи (a0, a1, a2, a3), где коэффициенты aii принадлежат
простому полю GF(2).
Таблица 2.1 |
7.2 |
|
0 |
= |
1 |
|
|
|
= |
(1000) |
|
|
|
|
|
|
|
|
1 |
= |
|
|
|
|
= |
(0100) |
|
|
|
|
|
|
|
|
2 |
= |
|
|
2 |
|
= |
(0010) |
|
|
|
|
|
|
|
|
3 |
= |
|
|
|
3 |
= |
(0001) |
4 |
= |
1 |
|
|
|
= |
(1100) |
5 |
= |
|
|
2 |
|
= |
(0110) |
6 |
= |
|
|
2 |
3 |
= |
(0011) |
|
|
|
|
|
|
|
|
7 |
= |
1 |
|
|
3 |
= |
(1101) |
|
|
|
|
|
|
|
|
8 |
= |
1 |
|
2 |
|
= |
(1010) |
|
|
|
|
|
|
|
|
9 |
= |
|
|
|
3 |
= |
(0101) |
10 |
= |
1 |
|
2 |
|
= |
(1110) |
11 |
= |
|
|
2 |
3 |
= |
(0111) |
12 |
= |
1 |
|
2 |
3 |
= |
(1111) |
13 |
= |
1 |
|
2 |
3 |
= |
(1011) |
14 |
= |
1 |
|
|
3 |
= |
(1001) |
15 |
= |
1 |
|
|
|
= |
(1000) |

7.3
Недвоичные циклические БЧХ - коды Рида-Соломона (РС). Построение циклических кодов РС.
Для кодов РС характерны все основные свойства циклических кодов БЧХ, за
исключением формирования порождающего многочлена G(х). .
Коды РС предназначены для исправления независимых t -кратных ошибок, т.е. t
ошибочных элементов поля, образованного примитивным многочленом P(x).
В качестве корней порождающего многочлена кода Рида-Соломона G(х) выбирают 2t последовательных элементов ε j, ε j+1,…, ε j+2t-1 поля Галуа GF(рm), где 1≤ j ≤ рm -1.
Часто принимают j=0 или1. Пусть j=0, тогда в качестве корней выбирают элементы
1, ε, ε 2,…, ε2t-1 . Тогда порождающий многочлен G(х) будет
2t 1 |
|
). |
|
|
|
G(x) (x |
i |
|
|
|
|
|
|
|
|
|
|
i 0 |
|
|
|
|
(3.1 ) |
|
|
|
|
|
|
Максимальная длина комбинации равна |
n 2 |
m |
1. |
||
|
|||||
|
|
|
|||
При этом все ненулевые элементы поля Галуа GF(2m) εi будут корнями двучленного
уравнения |
x |
n |
1 x |
2 |
m |
1 |
1 |
0. |
|
|
|
|
|||||
|
|
|
|
|
||||
Следовательно, порождающий многочлен G(х), в свою очередь, будет делителем |
||||||||
двучлена |
(x2m 1 1) |
|
|
|
|
|
|
|
Таким образом, вектор, представленный многочленом f(x), будет кодовым тогда и
только тогда, когда он делится без остатка порождающий многочлен G(х). .
Тогда для любого из корней 1, ε, ε2, ..., ε2t-1 справедливо уравнение |
7.4 |
||||||||||||||||
f(εi) = с |
0 |
+ с |
1 |
ε i + с |
(εi)2+ ... + с |
n-1 |
(εi)n 1 = |
0, c |
GF(2m) |
|
|||||||
|
|
|
|
|
|
2 |
|
|
|
|
i |
|
|
||||
которое можно записать в виде произведения двух матриц |
|
|
|||||||||||||||
|
[c |
0 |
c |
1 |
c |
2 |
… c |
n–1 |
]∙ [1 εi (εi)2…(εi) n 1 |
]T = 0. |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Но так как корнями f(х) должны быть все элементы 1, ε, ε2, ...,ε2t-1 , то можно
сделать вывод, что вектор [c0 c1 …c n–1] будет кодовым тогда и только тогда, когда
он принадлежит нулевому пространству матрицы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
... |
|
|
1 |
|
|
|
|
||
|
1 |
|
|
( 2 ) |
|
... |
( 2 )n 1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
2 |
( |
2 |
|
2 |
|
|
( |
2 |
|
n 1 |
|
|
||||
1 |
|
|
) |
|
|
... |
|
) |
|
|
. |
(3.2) |
|||||||
|
. |
|
. |
|
|
. |
|
|
|
... |
|
|
. |
|
|
|
|
||
|
|
|
2t 1 |
( |
2t 1 |
) |
2 |
... |
( |
2t 1 |
) |
n 1 |
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
То есть [c0 c1 c2 … c n–1]∙ HT=0
7.5
Корректирующие свойства кода PC определяются минимальным кодовым расстоянием dmin, которое для кодов PC является максимально достижимым и
равным dmin=2t + 1.
Более широкое применение на практике находят систематические коды PC,
поэтому ограничимся рассмотрением только систематических циклических
кодов PC.
3.1. Принципы кодирования и декодирования кодов Pида-Cоломона
Процесс кодирования для систематического кода PC осуществляется по тем же правилам, что и для любого циклического систематического кода − путем деления на порождающий многочлен G(x) и получения остатка, представляющего собой проверочные элементы.
|
|
|
|
|
|
кл |
|
|
|
|
|
1 |
2 |
ε6 |
ε5 |
|
|
ε5 |
ε2 |
|
x0 |
x1 |
|
|
x2 |
x3 |
|
|
ЯП |
ЯП |
2 |
ЯП3 |
ЯП4 |
|
|
1 |
|
|
|
|
|
Вход |
|
|
|
|
|
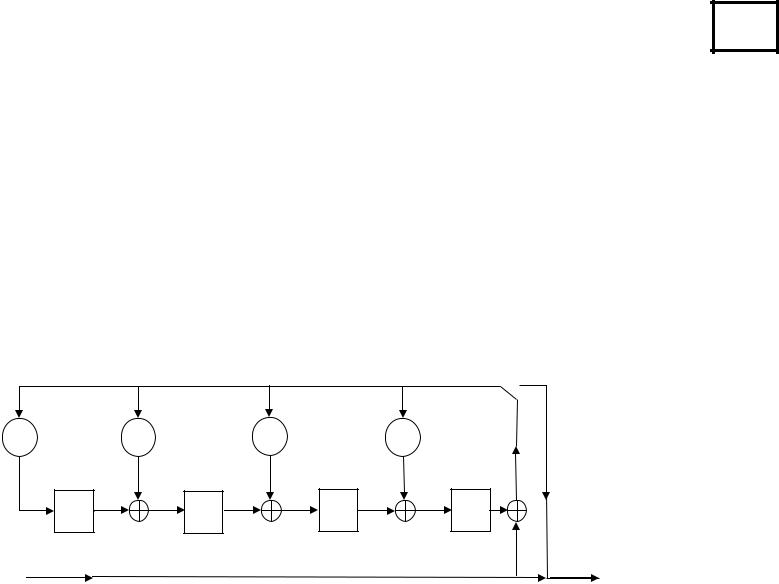
Выход |
Рис 4.1. Кодирующее устройство кода Рида-Соломона с t=2 и порождающим многочленом G(x)=(x +1)(x + ε)(x + ε2)(x + ε3) = ε6 + ε5 x+ ε5x2+ ε2x3+ x4 в поле GF(23)
