
вторая часть / практика / Пр6
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М.А. БОНЧ-БРУЕВИЧА» (СПБГУТ) Факультет информационных сетей и систем Кафедра сетей связи и передачи данных |
||||
|
||||
Практическая работа 6
|
||||
По дисциплине: |
Гетерогенные сети доступа |
|||
|
|
|||
Тема работы: |
Оценка потерь на трассе радиоканала в случае |
|||
|
дифракции на цилиндре |
|||
|
|
|||
|
||||
|
||||
Номер по списку: |
4 |
|
Работу выполнил студент |
|
|
|
|
группы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверил: |
|
|
|
|
Доцент кафедры ССиПД |
|
|
|
|
Владимиров Сергей Сергеевич |
|
Санкт-Петербург 2022 |
||||
Цель работы
Целью данной работы является ознакомление с механизмом дифракции радиосигнала на цилиндре и принципами оценки величины потерь, вызываемых данным типом дифракции. Выполнение
Выбрать из табл. 6.1 согласно своему номеру варианта исходные данные для расчета. Принять во внимание, что указана высота препятствия над уровнем моря.

Для заданных частоты f и расстояния b рассчитать (двумя способами, для каждого способа считать отдельно для гладкой поверхности с R = 1 и отдельно для неровной R = 0,65) и построить графики зависимости величины потерь на дифракцию на цилиндре в дБ от расстояния d = d1 +d2 при изменении расстояния a (диапазон 1–10 км, точки через 1 км) для высоты препятствия H = H + h0(a) (учесть кривизну земной поверхности). Для сравнения привести график потерь в свободном пространстве, посчитанный по формуле (3.3) для тех же расстояний d. Графики строить на одном рисунке (всего должно получиться пять кривых).
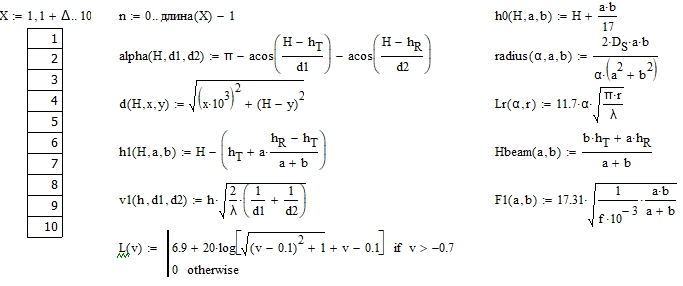
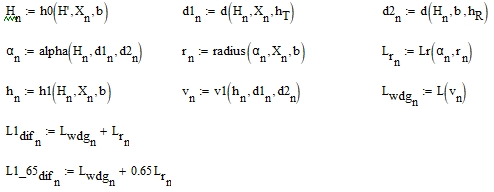
H, м |
d1, м |
d2, м |
α, рад. |
r, м |
Lr, дБ |
h, м |
v |
Lwdg, дБ |
70.353 |
1e3 |
6e3 |
0.024 |
298.417 |
16.407 |
20.496 |
1.896 |
18.614 |
70.706 |
2e3 |
6e3 |
0.015 |
853.25 |
17.951 |
23.206 |
1.623 |
17.388 |
71.059 |
3e3 |
6e3 |
0.013 |
1.386e3 |
18.777 |
25.392 |
1.538 |
16.975 |
71.412 |
4e3 |
6e3 |
0.011 |
1.791e3 |
19.061 |
27.212 |
1.505 |
16.808 |
71.765 |
5e3 |
6e3 |
0.011 |
2.052e3 |
18.977 |
28.765 |
1.492 |
16.744 |
72.118 |
6e3 |
6e3 |
0.01 |
2.191e3 |
18.668 |
30.118 |
1.49 |
16.732 |
72.471 |
7e3 |
6e3 |
9.693e-3 |
2.243e3 |
18.236 |
31.317 |
1.493 |
16.747 |
72.824 |
8e3 |
6e3 |
9.448e-3 |
2.235e3 |
17.745 |
32.395 |
1.499 |
16.778 |
73.176 |
9e3 |
6e3 |
9.271e-3 |
2.19e3 |
17.236 |
33.376 |
1.507 |
16.819 |
73.529 |
1e4 |
6e3 |
9.141e-3 |
2.124e3 |
16.733 |
34.279 |
1.516 |
16.867 |
L1dif, дБ |
L1_65dif, дБ |
35.022 |
29.279 |
35.339 |
29.056 |
35.752 |
29.18 |
35.869 |
29.198 |
35.722 |
29.08 |
35.4 |
28.866 |
34.982 |
28.6 |
34.523 |
28.312 |
34.055 |
28.023 |
33.6 |
27.743 |
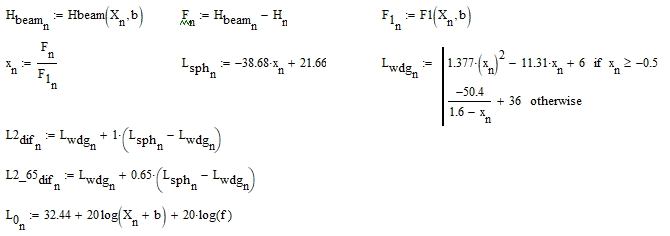
Hbeam, м |
F, м |
F1, м |
x |
Lsph, дБ |
Lwdg, дБ |
L2dif, дБ |
L2_65dif, дБ |
L0, дБ |
49.857 |
-20.496 |
15.28 |
-1.341 |
73.543 |
18.865 |
73.543 |
54.406 |
110.17 |
47.5 |
-23.206 |
20.214 |
-1.148 |
66.066 |
17.66 |
66.066 |
49.124 |
111.33 |
45.667 |
-25.392 |
23.341 |
-1.088 |
63.739 |
17.249 |
63.739 |
47.468 |
112.353 |
44.2 |
-27.212 |
25.569 |
-1.064 |
62.826 |
17.083 |
62.826 |
46.816 |
113.268 |
43 |
-28.765 |
27.256 |
-1.055 |
62.481 |
17.019 |
62.481 |
46.569 |
114.096 |
42 |
-30.118 |
28.587 |
-1.054 |
62.412 |
17.007 |
62.412 |
46.52 |
114.851 |
41.154 |
-31.317 |
29.666 |
-1.056 |
62.493 |
17.022 |
62.493 |
46.578 |
115.547 |
40.429 |
-32.395 |
30.56 |
-1.06 |
62.662 |
17.053 |
62.662 |
46.699 |
116.19 |
39.8 |
-33.376 |
31.315 |
-1.066 |
62.886 |
17.094 |
62.886 |
46.859 |
116.79 |
39.25 |
-34.279 |
31.961 |
-1.073 |
63.146 |
17.142 |
63.146 |
47.045 |
117.35 |

Для заданных частоты f и расстояния a рассчитать (двумя способами, для каждого способа считать отдельно для гладкой поверхности с R = 1 и отдельно для неровной R = 0,65) и построить графики зависимости величины потерь на дифракцию на цилиндре в дБ от расстояния d = d1 +d2 при изменении расстояния b (диапазон 1–10 км, точки через 1 км) для высоты препятствия H = H + h0(a) (учесть кривизну земной поверхности). Для сравнения привести график потерь в свободном пространстве, посчитанный по формуле (3.3) для тех же расстояний d. Графики строить на одном рисунке (всего должно получиться пять кривых).

H, м |
d1, м |
d2, м |
α, рад. |
r, м |
Lr, дБ |
h, м |
v |
Lwdg, дБ |
70.353 |
6e3 |
1.001e3 |
0.042 |
168.98 |
21.804 |
36.21 |
3.349 |
23.355 |
70.706 |
6e3 |
2e3 |
0.023 |
578.914 |
21.793 |
34.206 |
2.392 |
20.513 |
71.059 |
6e3 |
3e3 |
0.016 |
1.076e3 |
21.317 |
32.725 |
1.982 |
18.971 |
71.412 |
6e3 |
4e3 |
0.013 |
1.542e3 |
20.544 |
31.612 |
1.748 |
17.967 |
71.765 |
6e3 |
5e3 |
0.011 |
1.918e3 |
19.626 |
30.765 |
1.596 |
17.257 |
72.118 |
6e3 |
6e3 |
0.01 |
2.191e3 |
18.668 |
30.118 |
1.49 |
16.732 |
72.471 |
6e3 |
7e3 |
9.169e-3 |
2.371e3 |
17.736 |
29.624 |
1.412 |
16.33 |
72.824 |
6e3 |
8e3 |
8.532e-3 |
2.475e3 |
16.862 |
29.252 |
1.353 |
16.017 |
73.176 |
6e3 |
9e3 |
8.049e-3 |
2.523e3 |
16.06 |
28.976 |
1.308 |
15.77 |
73.529 |
6e3 |
1e4 |
7.674e-3 |
2.529e3 |
15.332 |
28.779 |
1.273 |
15.574 |
L1dif, дБ |
L1_65dif, дБ |
45.159 |
37.528 |
42.306 |
34.678 |
40.288 |
32.827 |
38.511 |
31.321 |
36.883 |
30.014 |
35.4 |
28.866 |
34.066 |
27.858 |
32.879 |
26.978 |
31.831 |
26.21 |
30.906 |
25.54 |
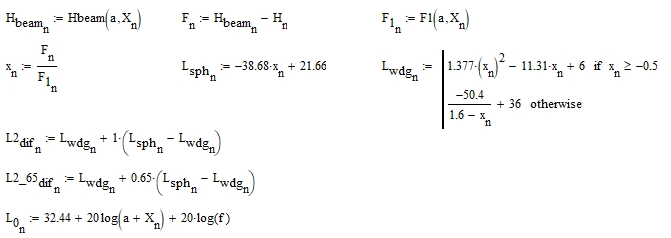
Hbeam, м |
F, м |
F1, м |
x |
Lsph, дБ |
Lwdg, дБ |
L2dif, дБ |
L2_65dif, дБ |
L0, дБ |
34.143 |
-36.21 |
15.28 |
-2.37 |
113.322 |
23.304 |
113.322 |
81.816 |
110.17 |
36.5 |
-34.206 |
20.214 |
-1.692 |
87.115 |
20.691 |
87.115 |
63.866 |
111.33 |
38.333 |
-32.725 |
23.341 |
-1.402 |
75.892 |
19.212 |
75.892 |
56.054 |
112.353 |
39.8 |
-31.612 |
25.569 |
-1.236 |
69.482 |
18.231 |
69.482 |
51.544 |
113.268 |
41 |
-30.765 |
27.256 |
-1.129 |
65.319 |
17.53 |
65.319 |
48.593 |
114.096 |
42 |
-30.118 |
28.587 |
-1.054 |
62.412 |
17.007 |
62.412 |
46.52 |
114.851 |
42.846 |
-29.624 |
29.666 |
-0.999 |
60.286 |
16.605 |
60.286 |
44.998 |
115.547 |
43.571 |
-29.252 |
30.56 |
-0.957 |
58.684 |
16.291 |
58.684 |
43.847 |
116.19 |
44.2 |
-28.976 |
31.315 |
-0.925 |
57.452 |
16.042 |
57.452 |
42.958 |
116.79 |
44.75 |
-28.779 |
31.961 |
-0.9 |
56.49 |
15.844 |
56.49 |
42.264 |
117.35 |
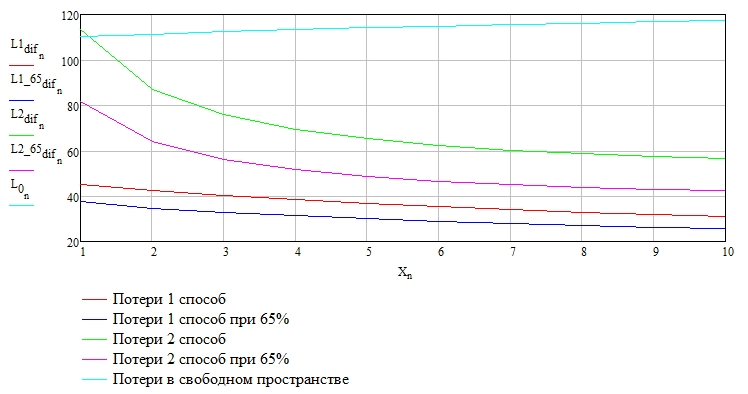
Выводы
Из полученных данных можно сделать вывод, что потери в свободном пространстве преобладают над потерями на дифракцию, которые обратно пропорциональны расстояниям до препятствий а и b.
