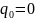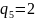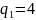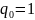ЭАиТЧ_ПР4

МИНОБРНАУКИ РОССИИ

Федеральное государственное образовательное учреждение высшего образования

“Юго–Западный государственный университет”

Кафедра информационной безопасности

Практическая работа №4

По дисциплине «Элементы алгебры и теории чисел»

По теме «Цепные дроби»

Выполнил: студент группы ИБ-11б

Гребенникова А.И.

Проверил проф. Добрица В.П.

Курск 2023г.

Цель: Познакомиться с понятиями цепных и подходящих дробей, способами их вычисления и применениями.

Ход работы:

Вариант 5.

Задание 1. Разложить простую дробь в правильную цепную дробь и найти все её подходящие дроби, если равно

Применим алгоритм Евклида:

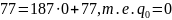
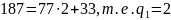
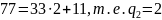
Таким образом (После ставится ;.) (Было: (После q₀ ставится ;.) (Почему убираете мои замечания?) Извиняюсь, видимо я пропустила письмо с вашим ответом, либо оно до меня не дошло по каким-то причинам, поэтому решила повторно отправить первоначальный вариант работы.

Составим таблицу вычисления подходящих дробей.

q
P	1	0	1	2	7
Q	0	1	2	5	17

Таким образом получаем

Задание 2. Сократить следующие дроби, пользуясь их разложением в цепную дробь

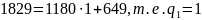
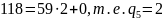
Таким образом

Составим таблицу вычисления подходящих дробей.

q
P	1	0	1	1	2	9	20
Q	0	1	1	2	3	14	31

Таким образом получаем

Подходящие дроби не сокращаются. В решении задачи мы получили, что , а значит, что исходная дробь сократима на 59.

(Было: (Как эти дроби связаны с исходным числом?). А значит надо ответ дать относительно всех дробей.) Пусть исходное число a. Тогда подходящие дроби 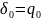, , … связаны с а следующим образом:

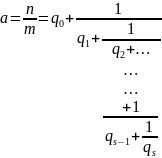
Кратко это принято записывать следующим образом:

(Имелось в виду как подходящие дроби связаны с исходным числом и между собой. Посмотрите свойства подходящих дробей.)

Для любого i 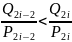и 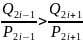, т.е. подходящие дроби с четными номерами только возрастают, а с нечетными – убывают.

Для i >1 выполняется равенство и неравенство

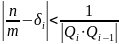
(Так пользуясь этим свойством, расположите все дроби и исходное число по возрастанию)

Задание 3. Найти значение несократимой дроби по значению цепной дроби:

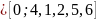
Составим таблицу для вычисления подходящих дробей.

q
P	1	0	1	1	3	16	99
Q	0	1	4	5	14	75	464

Таким образом получаем

Последняя подходящая дробь равна исходному числу, а подходящие дроби являются несократимыми дробями. Следовательно исходная дробь является несократимой.

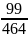
Сделаем проверку

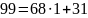
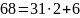
Ответ:

Задание 4. Разложить в цепную дробь и заменить подходящей дробью , если

Применим алгоритм Евклида

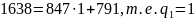
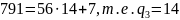
Составим таблицу для вычисления подходящих дробей.

q
P	1	1	2	3	44	355
Q	0	1	1	2	29	234

Таким образом получаем

Задание 5. Для задания № 1 с помощью подходящих дробей найти приближение к дроби с точностью до 0,001.

Чтобы получить точность 0,001 у нас должно быть произведение быть более, или равно 1000.

Таблица из задания 1.

q
P	1	0	1	2	7
Q	0	1	2	5	17

Будем находить эти произведения последовательно для разных i.

i=1: .

i=2: .

i=3: .

i=4: . (Но это же не дает требуемой оценки.) Но я никак не могу получить 1000 при и , это ведь последние элементы таблицы. (Но это не соответствует таблице.) Соответствует, по таблице и

q
P	1	0	1	2	7
Qi	Q0=0	Q1=1	Q2=2	Q3=5	Q4=17

Для оценки погрешности при замене дроби = подходящей дробью 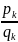используется формула:

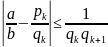
Данное условие выполняется при k=3.

Отсюда

(Было: Данное условие выполняется при k=3.

(Это неравенство выполняется только при k=3? На поставленный вопрос в задаче Вы не ответили.) Замечание осталось.) В моём случае данное неравенство выполняется и при других значениях k. Однако равенство 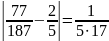выполняется только при k=3.

(Вам надо подобрать подходящую дробь такую, чтобы погрешность была меньше или равна 0,001.)

Если пользоваться методом подбора, то подходящая дробь, удовлетворяющая условию, равна

Ответ: 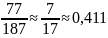(А что в первом случае приближенное равенство?)

Ошиблась, там строгое равенство. Дробь - это дробь , сокращенная на 11.

Ответ: