
ОТСС / О. А. Козлова, Л. П. Козлова 'Основы теориии сложных систем' ОТСС СПбГУТ бонч методичка
.pdf
−технологические защиты, обеспечивающие своевременное выявление факта возникновения аварийной ситуации и формирование управляющих воздействий, обеспечивающих защиту персонала и предотвращение повреждения оборудования.
К вспомогательным (сервисным) функциям относят:
−непрерывный автоматический контроль программных и технических средств и контроль выполнения информационной и управляющей функций АСУТП;
−самодиагностика программных и технических средств АСУТП, включая анализ отказов, неисправностей и ошибок оборудования АСУТП;
−обеспечения функционирования баз данных, включая нормативнотехническую;
−метрологический контроль и аттестацию информационных каналов;
−предоставление рекомендаций, справочной информации при настройке, наладке и эксплуатации программных и технических средств АСУТП;
−другие необходимые функции.
2.5. Типовые схемы управления АСУТП
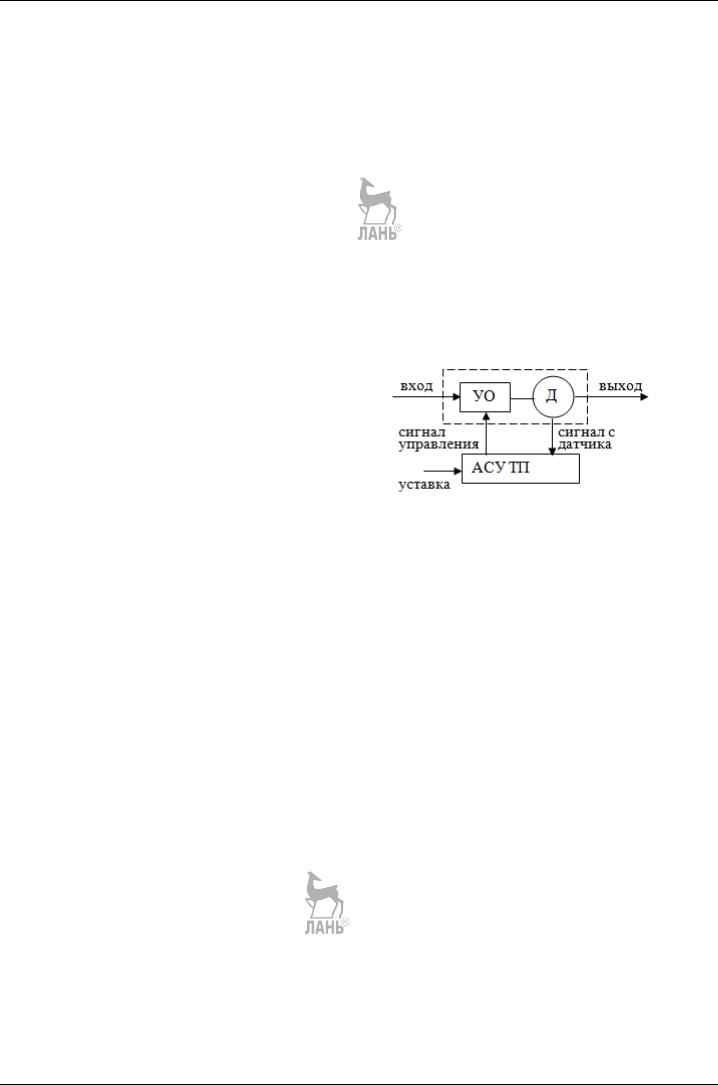
Управление в режиме сбора данных. Наиболее простой является схема управления технологическим процессом (ТП) в режиме сбора данных. При этом АСУ подсоединяется к процессу способом, выбранным ин- женером-технологом (рис. 2.6).
Интересующие инженера-технолога переменные преобразуются в цифровую форму, воспринимаемую системой ввода, и помещаются в задающее устройство ЭВМ. Величины на этом этапе являются цифровыми представлениями напряжения, генерируемого датчиками. Эти величины по соответствующим формулам преобразуются в технические единицы. Результаты вычислений регистрируются устройствами вывода АСУ ТП для последующего использования инженером-технологом.
Главной целью сбора данных является изучение ТП в различных условиях. В результате инженер-технолог получает воз-
можность построить и (или) уточнить математическую модель ТП, которым нужно управлять. При этом сбор данных не оказывает прямого воздействия на ТП и является осторожным подходом к внедрению методов управления, основанных на применении ЭВМ. Однако даже в самых сложных схемах управления ТП система сбора данных для целей анализа и уточнения модели ТП используется как одна из обязательных подсхем управления.
41

Рис. 2.7. Схема управления в режиме советчика оператора
Управление в режиме советчика опе-
ратора. Управление в режиме советчика предполагает, что ЭВМ в составе АСУТП работает в разомкнутом контуре, т. е. выходы АСУТП не связаны с органами, управляющими ТП. Управляющие воздействия фактически осуществляются оператором-техноло- гом, получающим указания от ЭВМ (рис. 2.7).
Все необходимые управляющие воздействия вычисляются ЭВМ в соответствии
смоделью ТП, результаты вычислений представляются оператору в печатном виде (или в виде сообщений на дисплее). Оператор управляет процессом, изменяя установки регуляторов. Регуляторы являются средствами поддержания оптимального управления ТП, причем оператор играет роль следящего и управляющего звена. АСУ ТП играет роль устройства, безошибочно и непрерывно направляющего оператора в его усилиях оптимизировать ТП. Основной недостаток этой схемы управления заключается в постоянном наличии человека в цепи управления. При большом числе входных и выходных переменных такая схема управления не может применяться из-за ограниченных психофизических возможностей человека. Однако управление этого типа имеет и преимущества. Оно удовлетворяет требованиям осторожного подхода к новым методам управления. Режим советчика обеспечивает хорошие возможности для проверки новых моделей ТП. АСУ ТП может следить за возникновением аварийных ситуаций, так что оператор имеет возможность уделять больше внимания работе
сустановками, при этом АСУ ТП следит за большим числом аварийных ситуаций, чем оператор.
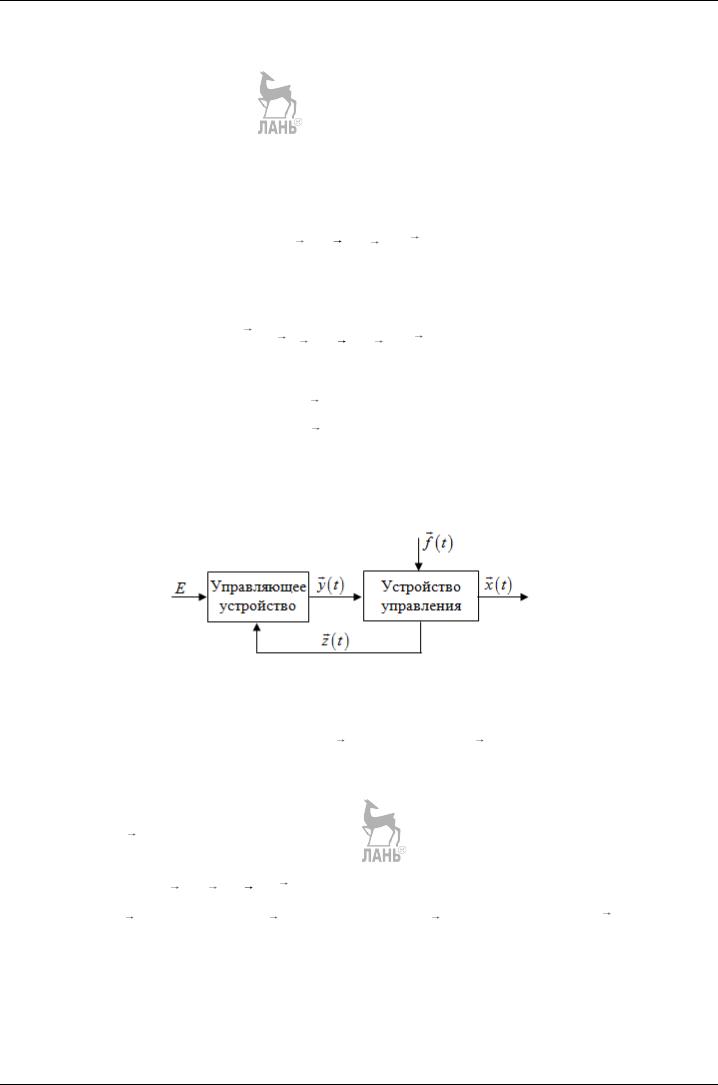
Супервизорное управление.
В этой схеме АСУ ТП используется в замкнутом контуре, т. е. установки регуляторам задаются непосредственно системой (рис. 2.8).
Задача режима супервизорно-
го управления – поддержание ТП вблизи оптимальной рабочей точки путем оперативного воздейст-
вия на него, что является одной из главных преимуществ данного режима. Работа входной части системы и вычисление управляющих воздействий мало отличается от работы системы управления в режиме советчика. Однако, после вычисленных значений установок, последние преобразовываются в величины, которые можно использовать для изменения настроек
42
регуляторов. Если регуляторы воспринимают напряжения, то величины, вырабатываемые ЭВМ, должны быть преобразованы в двоичные коды, которые с помощью цифроаналогового преобразователя превращаются в напряжения соответствующего уровня и знака. Оптимизация ТП в этом режиме выполняется периодически. Должны быть введены новые коэффициенты в уравнения контуров управления. Это осуществляется оператором посредством клавиатуры или считыванием результатов новых расчетов, выполненных на ЭВМ более высокого уровня. После этого АСУ ТП способна работать без вмешательства извне в течение длительного времени.
Пример АСУ ТП в супервизорном режиме. Управление автоматизированной транспортно-складской системы. ЭВМ выдает адреса стеллажных ячеек, а система локальной автоматики кранов-штабелеров отрабатывает перемещение их в соответствии с этими адресами.
Цифровое управление. В режиме непосредственного цифрового управления (НЦУ) (рис. 2.9) сигналы, используемые для приведения в действие управляющих органов, поступают непосредственно из АСУ ТП, и регуляторы вообще исключаются из системы. В сущности, регуляторы – это малые аналоговые вычислители, которые решают одно-единственное уравнение.
Концепция НЦУ позволяет заменить регуляторы с задаваемой установкой, АСУ ТП рассчитывает реальные воздействия и передает соответствующие сигналы непосредственно на управляющие органы.
Установки вводятся в АСУ оператором или ЭВМ, выполняющей расчеты по оптимизации процесса. При наличии системы НЦУ оператор должен иметь возможность изменять установки, контролировать некоторые избранные переменные, варьировать диапазоны допустимого изменения измеряемых переменных, изменять параметры настройки и вообще должен иметь доступ к управляющей программе. Одно из главных преимуществ режима НЦУ заключается в возможности изменения алгоритмов управления для контуров простым внесением изменений в хранимую программу. Наиболее очевидный недостаток НЦУ проявляется при отказе ЭВМ.
Вопросы для самопроверки
1.Дать определение АСУ.
2.Какова цель информационных систем?
3.Какие существуют виды информационных систем?
43

4.Какие функции осуществляет управляющая система?
5.Какие существуют разновидности управляющих систем?
6.Как подразделяются управляющие устройства по виду используемой информации ?
7.Как подразделяются АСУ по характеру изменения задающего воздействия?
8.Как подразделяются адаптивные АСУ?
9.Как подразделяются АСУ по характеру изменения параметров сиг-
налов?
10.Как классифицируются АСУ сложных систем?
11.Дайте определение АСУ ТП.
12.Из каких элементов состоит стандартная двухуровневая АСУ ТП?
13.Какие задачи может решать современная интегрированная АСУ?
14.Сколько уровней содержит современная интегрированная АСУ?
15.Какие существуют функции АСУ ТП.
16.Что относится к информационным функциям АСУ ТП?
17.Что относится к управляющим функциям АСУ ТП?
18.Что относится к вспомогательным функциям АСУ ТП?
44
3. ЛОКАЛЬНЫЕ ОПТИМИЗАТОРЫ И РЕГУЛЯТОРЫ
3.1. Обобщенная структура локального оптимизатора САУ
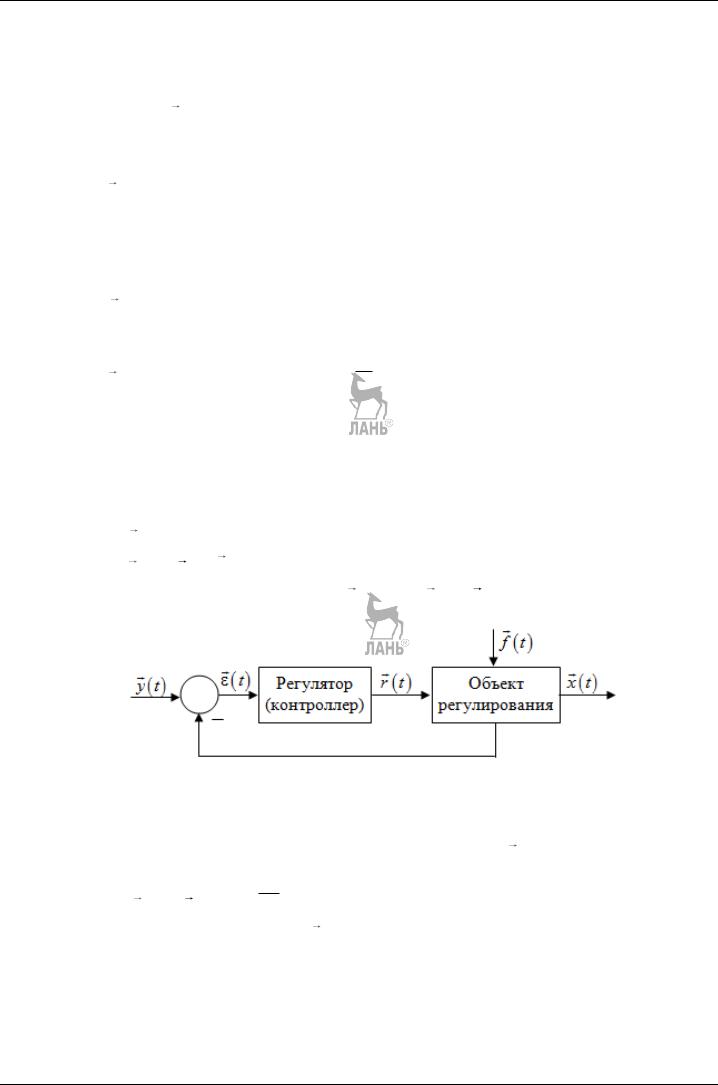
Пусть в структурной схеме локального оптимизатора (рис. 3.1) известны:
1. Цель управления (Е) в виде показателя – функционала
E E |
|
|
(3.1) |
|
x(t), y(t), z (t), f (t) ... |
2. Математическая модель (ММ) в виде системы дифференциальных уравнений
dx |
X x(t), y(t), z(t), |
f (t) ... |
(3.2) |
|
|||
|
|
|
|
dt
3. Ограничения:
x(t) A(t),
y(t) B(t),
(3.3)
A(t) X , B(t) Y.
Рис. 3.1. Структурная схема локального оптимизатора
Изменение векторов состояния x(t) , управления y(t) ограничено замк-
нутыми областями А и В, которые в свою очередь являются составляющими соответственно пространств состояний Х и управления Y.
Тогда задача управления состоит в определении такого вектора управления y(t) , который обеспечивал бы экстремум функционала (3.1) при известной ММ (3.2) и ограничениях (3.3).
При этом x(t), y(t), z(t), f(t) – многомерные векторные функции соответствия x(t) – состояния; y(t) – управления; z (t) – наблюдения; f (t) – возмущения.
45
Powered by TCPDF (www.tcpdf.org)
|
|
x1(t) |
|
|
|
|
|
|
|
|
|
|
x (t) |
|
|
|
|
|
|
|
|
То есть x(t) |
|
|
|
i 1, n , – переменные состояния. |
||||||
2 |
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
xn (t) |
|
|
|
|
|
|
|
|
z(t) z (t), z |
|
|
|
(t) T , i |
|
– наблюдаемые переменные, т. е. |
||||
2 |
(t), ..., z |
k |
1, k |
|||||||
1 |
|
|
|
|
|
|
|
|
||
переменные состояния, информация об изменении которых поступает в управляющую систему.
y1(t) |
|
|
|
|
|
|
|
|
|
|
|
y(t ) y2 |
(t) |
|
|
|
|
, |
i 1, m – управляющие воздействия (уставки); |
||||
|
|
|
|
|
|
... |
|
|
|
|
|
ym (t) |
|
|
|
|
|
f(t) f1(t), f2 (t), ..., fl (t) T , i 1,l – возмущающие воздействия.
3.2. Обобщенная структура локального регулятора САР
В обобщенной структурной схеме локального регулятора (рис. 3.2) известны:
1)y(t) – вектор входного воздействия;
2)r(t) [ (t), f (t)] – вектор регулирования;
3)показатель точности e (t) y(t) x(t) .
Рис. 3.2. Обобщенная структура локального регулятора
При известных параметрах, указанных выше, задача регулирования состоит в определении такого вектора регулирования r(t) (алгоритма), который обеспечивал бы минимум n частных показателей эффективности ei i yi (t) xi (t) , i 1, , каждый из которых зависит от одной из составляющих вектора ошибки ε(t) , при изменяющихся связях (3.2) и ограничениях (3.3).
46

Задача регулирования – это частный случай проблемы управления, а локальный регулятор является объектом локального оптимизатора
(рис. 3.1, 3.2).
3.2.1. Типовая функциональная схема локального регулятора
Типовая функциональная схема локального регулятора (рис. 3.3) состоит из преобразующего устройства (ПУ), последовательного корректирующего устройства (Пос. КУ), объекта управления (ОУ), объекта регулирования (ОР), параллельного корректирующего устройства (Пар. КУ) и датчика обратной связи (ДОС).
Рис. 3.3. Типовая функциональная схема локального регулятора
Локальные регуляторы содержат в своей структуре измерительные, усилительные, исполнительные и корректирующие устройства. Следовательно, САР – замкнутая динамическая система использования получающихся сигналов для управления источниками энергии, стремящаяся сохранить в допустимых пределах ошибки между требуемыми и действительными значениями регулируемых переменных путем их сравнения.
3.2.2. Основные типы локальных регуляторов
Классификация локальных регуляторов по приведенным признакам: 1. В зависимости от характера информации, используемой в регуляторе: а) с регулированием по разомкнутому циклу (рис. 3.4), т. е. по возму-
щениям.
Рис. 3.4. Регулирование по разомкнутому циклу
47

Задача состоит в определении регулирующего воздействия, где регулятор настраивается в зависимости от основного возмущения f(t).
«+»: высокое быстродействие, так как регулятор настраивается сразу по возмущению, а не так, как в случае регулирования по замкнутому циклу.
«–»: трудность программирования регулятора на возможные возмущения, следовательно, невысокая точность;
б) с регулированием по замкнутому циклу (рис. 3.5), т. е. по отклонениям.
Рис. 3.5. Регулирование по замкнутому циклу
«+»: в независимости от причин появления ошибки (t) система рабо-
тает по принципу ее (ошибки) компенсации.
«–»: быстродействие ниже, чем в случае с регулированием по разомкнутому циклу;
в) с комбинированным регулированием (рис. 3.6).
Рис. 3.6. Комбинированное регулирование
2. В зависимости от уставки y(t):
а) системы стабилизации y(t) = const;
б) программные системы y(t) = Y(t), причем Y(t) известно;
в) следящие системы y(t) = Y(t), причем Y(t) – заранее неизвестная функция.
3.В зависимости от размерности n вектора состояния x(t): а) одномерные n = 1;
б) двумерные n = 2; в) многомерные n = 3.
4.В зависимости от количества контуров в системе:
а) одноконтурные (используется только главная обратная связь, нет местных связей);
48

б) двухконтурные (используются одна главная и одна местная обратные связи);
в) многоконтурные (используются одна главная и много местных обратных связей).
5. В зависимости от установившегося значения ошибки:
а) статические lim (t) const 0 ;
t
б) астатические lim (t) 0 .
t
Система называется астатической по управляющему (или возмущающему) воздействию, если при подаче на вход постоянного управляющего (или возмущающего) воздействия ошибка в установившемся состоянии не зависит от величины этого воздействия и равна нулю.
6. В зависимости от характеров сигналов, циркулирующих в системе: а) непрерывные; б) импульсные; в) релейные;
г) релейно-импульсные (кодово-импульсные); д) на переменном токе (с гармонической модуляцией).
Вопросы для самопроверки
1.Какие элементы включает локальный оптимизатор?
2.Запишите цель управления в виде функционала оптимизатора.
3.Запишите математическую модель в виде системы дифференциальных уравнений.
4.Какие элементы включает обобщенная схема локального регулятора?
5.Какие существуют основные виды локальных регуляторов?
6.По каким признакам классифицируются регуляторы.
7.Приведите схему регулирования по разомкнутому циклу.
8.Приведите схему регулирования по замкнутому циклу.
9.Как подразделяются регуляторы в зависимости от уставки y(t) ?
10.Как подразделяются регуляторы в зависимости от размерности n вектора состояния x t ?
11.Как подразделяются регуляторы в зависимости от количества контуров в системе?
12.Как подразделяются регуляторы в зависимости от установившегося значения ошибки?
13.Какая система называется астатической?
14.Как подразделяются регуляторы в зависимости от характеров сигналов, циркулирующих в системе?
49

4. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СЛОЖНЫХ СИСТЕМ 4.1. Основные виды математических моделей
Математические модели (ММ) сложных систем подразделяются на линейные и нелинейные.
В свою очередь каждая из ММ может быть:
1)непрерывной (система дифференциальных или интегро-дифферен- циальных уравнений);
2)дискретной (система разностных уравнений);
3)дискретно-непрерывной (сочетание непрерывной и дискретной систем).
В свою очередь каждая из них может быть стационарной и нестационарной.
Математическая модель нестационарна, если хотя бы один из параметров системы изменяется с течением времени.
В свою очередь каждая из них может быть:
1)с сосредоточенными параметрами;
Физические параметры системы (например, масса, скорость, потенциал и др.) обычно сосредоточены в точке (так можно считать), коэффициенты дифференциальных уравнений зависят от этих параметров. В результате, математическая модель будет, например, системой дифференциальных
d
уравнений в полных производных ;
dt
2) с сосредоточенными и распределенными параметрами.
Если система содержит одну из подсистем (например, канал связи, трубопровод), параметры которой распределены в пространстве, то математическая модель такой системы будет содержать, например, систему
дифференциальных уравнений в частных производных .
t
В свою очередь каждая из них может быть детерминированной и стохастической или со случайными параметрами (если хотя бы один из параметров или воздействий является случайной функцией или величиной).
4.2. Описание систем управления моделями пространства состояний
4.2.1. Уравнения состояния САУ
Пространство состояний САУ – это бесконечная совокупность временных моментов состояния системы, описанная конечной совокупностью переменных состояния.
50
