Молчанов (ответы) / 7. Оценка вероятности потерь в системе с ожиданием (вторая формула Эрланга)

Для систем с ожиданием вероятность ожидания для поступившего вызова p(γ > 0) – это отношение математических ожиданий числа задержанных в обслуживании за отрезок времени [t₁,t₂] вызовов к числу поступивших за рассматриваемый промежуток времени вызовов находится из выражения:

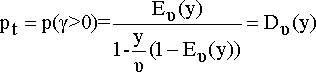,                        (6.2)

Выражение (6.2) называется второй формулой Эрланга. Формула табулирована. Таблицы позволяют по любым двум из трех параметров y, υ, p_t – определить третий. Выражение (6.2) показывает, что потери по времени p_t , численно равные условным потерям p(γ > 0), могут быть определены и с помощью таблиц первой формулы Эрланга. Используя эти таблицы, p_t можем определить из следующего соотношения:

.

Потери измеряются в процентах или в промилле [0,1%]. Нормативы: На ГТС между двумя ТА на одной ГТС  р ≤ 0,03; на ЗТС между двумя ТА разных местных сетей одной зоны р ≤ 0,03 – 0,13; на МТС между двумя ТА разных зон семизначной нумерации р ≤ 0,1. Если потери меньше 10 %, то абоненты на них не реагируют. Основная задача инженерных расчетов – установление оптимального количества обслуживающих приборов при заданной интенсивности нагрузки и качестве обслуживания: V = f [Y, р].