

Лекция 5. Непрерывность функции
5-1 Понятие непрерывности функции
5-2 Свойства функций, непрерывных на отрезке
5-3 Точки разрыва
23 сентября 2007 г.

Эпиграф
Я знаю, что это такое, только
до той поры, пока меня не
спросят – что это такое!
Блаженный
Августин
© Иванов О.В., Кудряшова Л.В., 2005
2

5-1.
Понятие непрерывности функции
Определение на языке пределов
Определение на языке приращений
Непрерывность на промежутке
23 сентября 2007 г.

Интуитивное определение непрерывности
Если линию можно построить, не отрывая карандаша от бумаги,
эта линия непрерывна.
Наше интуитивное представление о непрерывности следует
подкрепить точными математическими определениями.
Существует два определения непрерывности функции: на языке
пределов и на языке приращений. Мы рассмотрим их, а затем
убедимся в их эквивалентности.
© Иванов О.В., Кудряшова Л.В., 2005
4

Определение непрерывности
Функция f (x) называется непрерывной в точке a, если:
1)функция f (x) определена в точке a,
2)имеет конечный предел при x → a,
3)этот предел равен значению функции в этой точке:
lim f (x) = f (a)
x→a
© Иванов О.В., Кудряшова Л.В., 2005
5
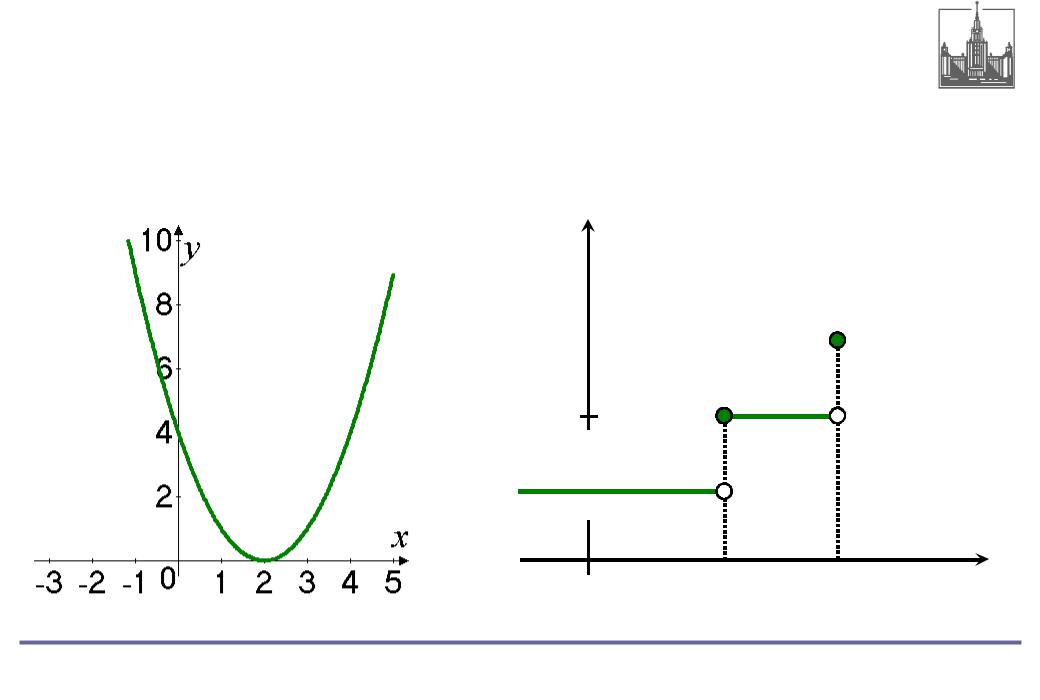
Примеры
|
|
|
|
|
|
|
Непрерывная функция |
Не непрерывная функция |
|||
|
|
(разрывная) |
|||
|
|
y |
|||
|
|
|
|
|
|
4
2 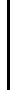
x
a b
© Иванов О.В., Кудряшова Л.В., 2005
6
Второе определение непрерывности
Функция f (x) называется непрерывной в точке a, если она определена в этой точке и бесконечно малому приращению
аргумента |
соответствует |
бесконечно |
малое |
приращение |
||
функции: |
lim ∆y = 0 |
|
|
|
||
|
∆x→0 |
|
|
|
|
|
Приращение функции: |
|
f (a+∆ x) |
y |
y=f (x) |
||
|
|
|
|
|||
∆ y = f (a+∆ x) – f (a) |
|
∆ y |
|
|
||
|
|
|
|
|||
|
|
|
f (a) |
|
|
|
Определение означает, что |
|
|
|
|
||
|
|
|
∆ x |
|
||
при ∆ x → 0 |
|
|
|
|
||
|
0 |
a |
a+∆ x x |
|
||
∆ y → 0 |
|
|
||||
|
|
|
||||
© Иванов О.В., Кудряшова Л.В., 2005
7
Доказательство эквивалентности
Докажем равносильность двух определений непрерывности.
1 lim f (x) = f (a) |
lim ( f (x) − f (a)) = 0 |
|
x→a |
|
x−a→0 |
lim |
( f (a +∆x) − f (a)) = 0 |
|
(a+∆x−a)→0 |
|
|
|
|
|
lim ∆y = 0 |
2 |
|
∆x→0 |
|
|
|
|
|
© Иванов О.В., Кудряшова Л.В., 2005
8

Непрерывность на промежутке
Функция f (x) называется непрерывной на промежутке X, если она непрерывна в каждой точке этого промежутка.
Утверждение. Все элементарные функции непрерывны в
области их определения.
© Иванов О.В., Кудряшова Л.В., 2005
9

Непрерывность функции x2
Используем для доказательства непрерывности определение 2.
∆y = (x +∆x)2 − x2
lim ∆y = lim (x2 +2x ∆x +(∆x)2 − x2 ) =
∆x→0 ∆x→0
= lim (2x ∆x +(∆x)2 ) = 0
∆x→0
Получили, что функция x2 непрерывна.
Задание. Докажите непрерывность функции sin x.
© Иванов О.В., Кудряшова Л.В., 2005
10
