5.3. Описание идеи расчета

Как пример решения прямой постановки используем задачу из английского учебника [10]. В ее решении заложены 2 основные формулы.

Для случая, когда для поверхности заданы потоки 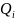[10]:

Поверхности с заданными температурами [10]:

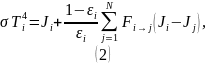
В которых, если переводить на наше обозначения: 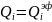, , 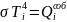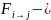угловой коэффициент 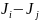– поток эффективного излучения с i на j поверхность.

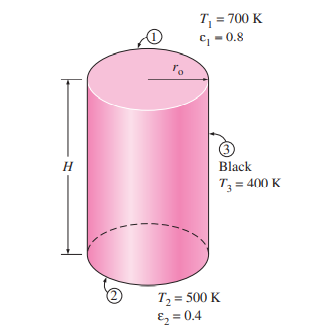
Рисунок 2 – цилиндрический объект для решения условной задачи [10]

Рассмотрим цилиндрический объект с , как показано на рисунке 2. Верхняя часть (поверхность 1) и основание (поверхность 2) цилиндра имеют степень черноты 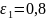и 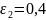соответственно и поддерживаются при постоянных температурах 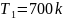и 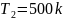. Боковая поверхность вплотную приближается к абсолютно черному телу и поддерживается при температуре 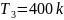. Необходимо определить суммарную скорость теплопередачи излучения на каждой поверхности во время стационарной работы и объясните, как можно поддерживать эти поверхности при заданных температурах.

Решение [10]: на поверхностях цилиндра поддерживается равномерная температура. Необходимо определить суммарную скорость теплопередачи излучения на каждой поверхности во время стационарной работы.

Допущения:

1. Существуют устойчивые условия эксплуатации.

2. Поверхности непрозрачные и серые.

3. Конвекционный теплообмен не учитывается.

Анализ: мы будем решать эту проблему систематически, используя прямой метод, чтобы продемонстрировать его применение. Цилиндр можно рассматривать как корпус с тремя поверхностями, площадь поверхности которого составляет [10]:

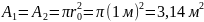
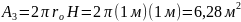
Далее определим угловой коэффициент от основания до верхней поверхности, как видно из рисунка 2.1 [10]:

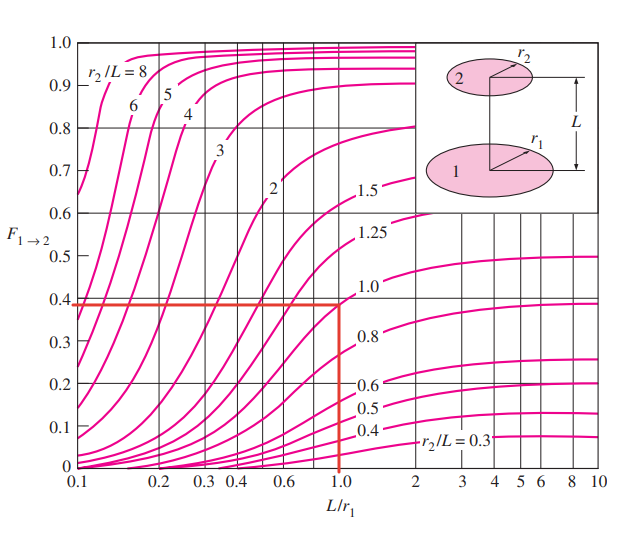
Рисунок 2.1 – номограмма угловых коэффициентов для двух [10] параллельных круглых поверхностей. В данной задаче соотношение 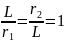, соответственно

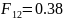
Затем угловой коэффициент от основания до боковой поверхности определяется путем применения правила суммирования, которое имеет следующий вид [10]:

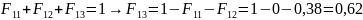
поскольку базовая поверхность плоская и, следовательно, 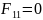. Отмечая, что верхняя и нижняя поверхности симметричны относительно боковой поверхност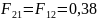и, и 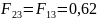. Угловой коэффициент 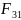определяется из соотношения взаимности [4,6,10]:

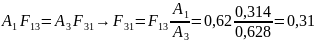
Кроме того, 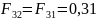из-за симметрии. Теперь, когда доступны все угловые коэффициенты, мы применяем уравнения 12-35 к каждой поверхности, чтобы определить радиусы [10]:

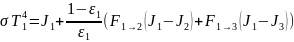
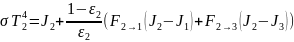
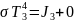
Подставляя известные величины получим:

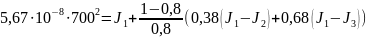
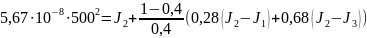
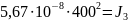
Решение для приведенных выше дает:

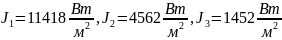
И из полученных потоков можно найти необходимое количество теплоты для каждой поверхности:

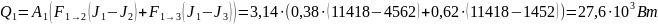
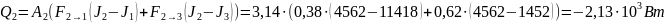
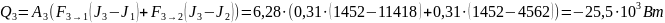
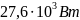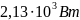Полученные значения показывают какое количество тепла необходимо подвести/отвести от поверхностей: на первую (верхнюю) поверхность необходимо непрерывно подавать , со 2 (нижней) поверхности отводить и также отводить тепло от 3 (боковой) поверхности

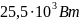
Данный пример представляет собой прямое решение задачи радиационного теплообмена. В нашем же случае будет поставлена обратная задача, то есть зная только мощность (результирующий поток) греющей поверхности сможем найти температуры всех поверхностей.