Лаб_10

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Санкт-Петербургский государственный университет телекоммуникаций

им. проф. М.А. Бонч-Бруевича»

(СПБГУТ)

__________________________________________________________________

Факультет ИКСС

Кафедра ЗСС

Отчет к лабораторной работе № 10 по дисциплине:

«Математические основы защиты информации»

Тема: «Квадратичные сравнения»

Выполнил студент Группа ИКБ-14:

Травкина Е. А.

Проверил:

Кушнир Д.В.

г. Санкт-Петербург

2023

Квадратичные сравнения

Рассмотрим случай x^2=a mod n

Частный случай. Сравнение по модулю простого числа p.

x^2=a mod p. (p-простое, a-целое, НОД(a,p)=1).

Такое сравнение имеет либо два решения, либо не имеет решений.

Пример x^2=3 mod 11 => решения x=5 mod 11 и x=-5 mod 11 (-5=6 mod 11). Т.о. решения 5 и 6.

Пример x^2=2 mod 11 => не имеет решения.

В уравнении

x^2=a mod p, a- называют квадратичным вычетом, если уравнение имеет решения; a- называют квадратичным невычетом, если уравнение не имеет решения. Если p – простое, то (p-1)/2 элементов поля Z_p квадратичные вычеты и (p-1)/2 – квадратичные невычеты.

Пример:

p=7, Z*₇={1,2,3,4,5,6} (все ненулевые элементы)

1²=1 mod 7 2²=4 mod 7 3²=2 mod 7 4²=2 mod 7 5²=4 mod 7 6²=1 mod 7

Числа 1,2,4 – квадратичные вычеты, а числа 3,5,6 – квадратичные невычеты.

Символ Лежандра

Определение. Для любого простого нечётного «p» и целого «a» символ Лежандра определяется как:

0, если a=0 mod p = 1, если «a» квадратичный вычет по mod p -1, если «a» квадратичный невычет по mod p

Свойства символа Лежандра (см. лекции)

Алгоритм вычисления символа Лежандра (см. лекции)

Критерий Эйлера. (позволяет определить, является ли число a по mod p квадратичным вычетом или невычетом)

Если a^(p-1)/2 = 1 mod p, то «a» – квадратичный вычет по модулю «p».

Если a^(p-1)/2 = -1 mod p, то «a» – квадратичный невычет по модулю «p».

При составном «n» возможно получение значения a^(n-1)/2 = 0 mod n, что означает, что «a» делит «n» (уравнение не имеет решений).

Т.о. один из способов вычисления символа Лежандра:

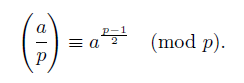
Решение квадратичного сравнения (модуль – простое).

Случай 1. p = 4k+3, т.е. p=3 mod 4, тогда:

X₁= a^(p+1)/4 mod p и X₂= - a^(p+1)/4 mod p

Пример.

x^2=3 mod 23. Решение: x=±16 mod 23. x^2=1 mod 11. Решения нет.

Случай 2. p = 4k+1. (Решение относительно сложное – в данной работе не будет рассмотрено)

Решение квадратичного сравнения (модуль – составной).

Квадратичное сравнение по составному модулю может быть приведено к решению системы сравнений по модулю в виде простого числа. Другими словами, мы можем анализировать x^2=a mod n, если имеем разложение n на множители. Теперь мы можем решить каждое анализируемое уравнение (если оно разрешимо) и найти k пар ответов для x.

Пример:

X^2=36 mod 77; 77=7*11.

X^2=36 mod 7=1 mod 7 X^2=36 mod 11=3 mod 11.

Так как каждое из чисел 7 и 11, являются числами вида 4k+3, то возможно использовать указанный выше способ решения.

Далее необходимо проверить, что 1 и 3 квадратичные вычеты. Проверка выполняется (a^(p-1)/2 = 1 mod p) и далее решаем каждое уравнение в отдельности, получаем: x=±1 mod 7 и x=±5 mod 11

В итоге формируется 4-ые отдельные системы, каждая из которых даст по одному ответу. Ответ находим по модулю 77.

Система 1: x= +1 mod 7 и x= +5 mod 11 => x= -6 = 71 mod 77; Система 2: x= +1 mod 7 и x= -5 mod 11 => x=-27 = 50 mod 77; Система 3: x= -1 mod 7 и x= +5 mod 11 => x= 27; Система 4: x= -1 mod 7 и x= -5 mod 11 => x= 6.

Итоговый ответ x=±6 и x=±27

Задание.

Задание 1. Выбрать простое число большее 30-ти из набора:.

Вариант 23(3)

P = 41

(p-1)/2 = 20

1	1
2	4
3	9
4	16
5	25
6	36
7	8
8	23
9	40
10	18
11	39
12	21
13	5
14	32
15	20
16	10
17	2
18	37
19	33
20	31

Вычеты: 1 2 4 5 8 9 10 16 18 20 21 23 25 31 32 33 36 37 40

Невычеты: 3 6 7 11 12 13 14 15 17 19 22 24 26 27 28 29 30 34 35 38 39

Задание 2. Студент с номером 23(3), выбирает числа p: 300<p>400

4*78+1 = 313. Числа меньше половины: 153, 154, 155, 156. Числа больше половины: 157, 158, 159, 160.

4*82+3 = 331. Числа меньше половины: 162, 163, 164, 165. Числа больше половины: 166, 167, 168, 169.

Для числа 313	Квадрат числа	Остаток (mod 313)	Символ Лежандра
153	23409	247	-1
154	23716	241	-1
155	24025	237	1
156	24336	235	1
157	24649	235	1
158	24964	237	1
159	25281	241	-1
160	25600	247	-1

Для числа 331	Квадрат числа	Остаток (mod 331)	Символ Лежандра
162	26244	95	-1
163	26569	89	1
164	26896	85	-1
165	27225	83	1
166	27556	83	-1
167	27889	85	1
168	28224	89	-1
169	28561	95	1

Пример расчёта символа Лежандра для a = 153 p = 313

153/313 = (-1)^(((313-1)/2)*((153-1)/2)) * (313/153) = 313/153 = 7/153 = (-1)^(((7-1)/2)*((153-1)/2)) * (153/7) = 153/7 = 6/7 = (-1)^((7^2-1)/8) * (6/7) = 3/7 = (-1)^(((7-1)/2)*((3-1)/2)) * (3/7) = 7/3 = -1/3 = -1

Вывод:

Видно, что для числа вида 4*k+1 числа а повторяются при переходе от чисел меньше половины числа p, к числам больше половины числа p. Символы Лежандра чередуются и “зеркально отражаются” при переходе от чисел меньше половины числа p, к числам больше половины числа p.

В случае числа вида 4*k+3 при переходе числа а “зеркально отражаются”. Символы Лежандра в каждой половине чередуются “два через два”, и при переходе из одной половине к другой эта последовательность “инвертируется”.

Задание 3. Решаем ДВА квадратичных сравнения.

p = 47, a = 2; a = 3.

x^2 = 2 mod 47

x = ± 2^(47+1/4) mod 47 = ± 7 mod 47

x^2 = 3 mod 47

x = ± 3^(48/4) mod 47 = ± 12 mod 47

Задание 4. Решить квадратичное сравнение по составному модулю.

Выбрать составной модуль. Сомножители составного модуля должны быть двумя простыми числами вида 4k+3.

Параметр «а» выбираем самостоятельно, по двум условиям:

1. квадратичное сравнение по каждому сомножителю составного модуля должно иметь решение;

2. число «a» не должно иметь общих множителей ни с одним из сомножителей составного модуля.

Далее решить составленное квадратичное сравнение по составному модулю.

n = 133

x^2 = 36 mod 133;

133 = 7*19

x^2 = 36 mod 7 = 1 mod 7 x^2 = 36 mod 19 = 17 mod 19

x = ± 1 mod 7 и x = ± 6 mod 19

Система 1:

x = +1 mod 7 и x = +6 mod 19 => x = - 13 = 120 (mod 133)

Система 2:

x = +1 mod 7 и x = -6 mod 19 => x = -6 = 127 (mod 133)

Система 3: x = -1 mod 7 и x = +6 mod 19 => x = 6

Система 4: x = -1 mod 7 и x = -6 mod 19 => x = 13 Ответ: x = ±6 и x = ± 13

n = 319

4л+3 = 319

x^2 = 36 mod 319;

341 = 11*31

x^2 = 36 mod 11 = 3 mod 11

x^2 = 36 mod 31 = 5 mod 31

x = ± 3 mod 11 и x = ± 6 mod 19

Система 1:

x = +1 mod 7

x = +6 mod 19 => x = - 13 = 120 (mod 133)

Система 2:

x = +1 mod 7

x = -6 mod 19 => x = -6 = 127 (mod 133)

Система 3:

x = -1 mod 7

x = +6 mod 19 => x = 6

Система 4:

x = -1 mod 7

x = -6 mod 19 => x = 13

Ответ: x = ±6 и x = ± 13

9