
Практика
.pdfпроизводства продукции (х1, х2), обеспечивающий максимальную прибыль
при реализации продукции:
F 2x |
4x |
2 |
max |
1 |
|
|
при ограничениях:
3х |
5х |
2 |
40 |
||||
|
|
1 |
|
|
|
||
2 |
х |
х |
|
|
15 |
||
|
2 |
|
|||||
|
1 |
|
|
|
|
||
|
4 |
х |
х |
|
|
28 |
|
|
2 |
|
|||||
|
1 |
|
|
|
|
||
х |
0, х |
2 |
0 |
||||
|
1 |
|
|
|
|
||
Математическая модель исходной задачи составлена.
2) Решим исходную задачу симплексным методом.
Приведем задачу к канонической форме.
Чтобы перейти от общей формы записи ЗЛП к канонической, нужно
ограничения-неравенства исходной ЗЛП преобразовать в ограничения-
равенства добавлением к их левой части дополнительной неотрицательной переменной со знаком «+» в случае неравенства вида « » и со знаком «-» - в
случае неравенства вида « ».
В первое ограничение системы добавим переменную |
x |
3 |
со знаком «+», |
||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
во второе ограничение системы добавим переменную |
x |
4 |
со знаком «+» и в |
||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
третье ограничение |
системы добавим переменную x5 |
|
со |
|
знаком «+». В |
||||||||
результате получаем следующую систему ограничений: |
|
|
|
|
|
|
|||||||
3х1 5х2 х3 40 |
|
|
|
|
|
|
|||||||
|
|
|
х2 |
х4 15 |
|
|
|
|
|
|
|||
2х1 |
|
|
|
|
|
|
|||||||
4х |
х |
2 |
х |
5 |
28 |
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
||
х |
j |
0, |
|
j 1,...,5 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, исходная задача может быть записана в канонической
форме так: найти максимум функции
F 2x |
4x |
2 |
max |
1 |
|
|
при ограничениях:
3х1 5х2 х3 40 |
|||||||
|
|
|
х2 |
х4 |
|
||
2х1 |
15 |
||||||
4х |
х |
2 |
х |
5 |
28 |
||
|
|
1 |
|
|
|
||
х |
j |
0, |
|
j 1,...,5 |
|||
|
|
|
|
|
|
|
|
В полученной системе уравнений системы ограничений имеются три базисные переменные. Решим систему уравнений относительно базисных переменных x3, x4 и x5. Запишем базисное решение в стандартной форме:
х3 40 3х1 5х2х4 15 2х1 х2х5 28 4х1 х2
или
Х |
0 |
|
0; 0;
40; 15;
28
.
Составим симплекс-таблицу:
Базис |
Свободный |
x1 |
x2 |
x3 |
x4 |
x5 |
|
член |
|||||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x3 |
40 |
3 |
5 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
x4 |
15 |
2 |
1 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
x5 |
28 |
4 |
1 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
F(X0) |
0 |
-2 |
-4 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
Переходим к основному алгоритму симплекс-метода.
Итерация 1. Текущий опорный план не является оптимальным, так как в индексной строке находятся отрицательные коэффициенты.

В индексной строке F(х) выбираем максимальный отрицательный элемент. В качестве генерального столбца будет выступать x2. Вычислим значения Di по строкам как частное от деления: bi / ai2 и из них выберем наименьшее:
min |
|
40 |
; |
15 |
; |
|
|
5 |
1 |
||||
|
|
|
||||
|
|
|
|
1
8
.
Таким образом, строка х3 является генеральной. Разрешающий элемент равен РЭ = 5 и находится на пересечении генерального столбца и генеральной строки.
Формируем следующую часть симплексной таблицы. Вместо переменной x3 в план 1 войдет переменная x2.
Строка, соответствующая переменной x2 в плане 1, получена в результате деления всех элементов строки x3 плана 0 на разрешающий элемент РЭ=5. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули. Таким образом, в новом плане 1
заполнены строка x2 и столбец x2.
Все остальные элементы нового плана, включая элементы индексной строки, определяем по правилу прямоугольника.
Элементы разрешающей строки делим на разрешающий элемент и записываем в соответствующей по номеру строке новой таблицы:
a |
|
arj |
|
|
, при i = r. |
||
rj |
|
|
|
|
|
ark |
|
Все остальные элементы новой таблицы рассчитываем по формулам:
aij/ aij |
|
aik arj |
, |
при i ≠ r |
|
ark |
|||||
|
|
|
|

где |
a |
/ |
- элемент новой симплекс-таблицы, aij, - элемент предыдущей |
|
ij |
||||
|
симплекс-таблицы, ark - разрешающий элемент , aik - элемент разрешающего столбца, arj - элемент разрешающей строки.
Представим расчет каждого элемента в виде таблицы:
|
Свободный член |
|
x1 |
|
x2 |
||
|
|
|
|
|
|
|
|
40 / 5 |
|
3 / 5 |
|
|
5 / 5 |
|
|
|
|
|
|
|
|
|
|
15-(40 * 1)/5 |
|
2-(3 * 1)/5 |
|
|
1-(5 * 1)/5 |
|
|
|
|
|
|
|
|
|
|
28-(40 * 1)/5 |
|
4-(3 * 1)/5 |
|
|
1-(5 * 1)/5 |
|
|
|
|
|
|
|
|
|
|
0-(40 * (-4))/5 |
|
-2-(3 * (-4))/5 |
|
-4-(5 * (-4))/5 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
x4 |
|
|
x5 |
|
|
|
|
|
|
|
||
|
1 / 5 |
0 / 5 |
|
0 / 5 |
|
||
|
|
|
|
|
|
||
|
0-(1 * 1)/5 |
1-(0 * 1)/5 |
|
0-(0 * 1)/5 |
|
||
|
|
|
|
|
|
||
|
0-(1 * 1)/5 |
0-(0 * 1)/5 |
|
1-(0 * 1)/5 |
|
||
|
|
|
|
|
|
||
|
0-(1 * (-4))/5 |
0-(0 * (-4))/5 |
|
0-(0 * (-4))/5 |
|
||
|
|
|
|
|
|
|
|
После перерасчета получаем новую таблицу:
Базис |
Свободный член |
x1 |
x2 |
x3 |
x4 |
x5 |
|
|
|
|
|
|
|
x2 |
8 |
0,6 |
1 |
0,2 |
0 |
0 |
|
|
|
|
|
|
|
x4 |
7 |
1,4 |
0 |
-0,2 |
1 |
0 |
|
|
|
|
|
|
|
x5 |
20 |
3,4 |
0 |
-0,2 |
0 |
1 |
|
|
|
|
|
|
|
F(X1) |
32 |
0,4 |
0 |
0,8 |
0 |
0 |
|
|
|
|
|
|
|
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальное решение задачи.
Таким образом, получаем:

|
Х |
опт |
0; 8 |
; |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
Fmax |
F 0; 8 2 0 4 8 32 . |
||||||||
Ответ. |
Х |
опт |
0; 8 |
; |
F |
32 |
. Для получения максимальной прибыли от |
|||
|
|
|
|
max |
|
|||||
реализации выпускаемой продукции на предприятии необходимо производить 8 единиц продукции вида П2, а продукцию вида П1 производить не требуется. При использовании данного плана выпуска продукции предприятие получит наибольшую прибыль, которая составит 32 ден.ед.
РЕШЕНИЕ ГРАФИЧЕСКИМ СПОСОБОМ:
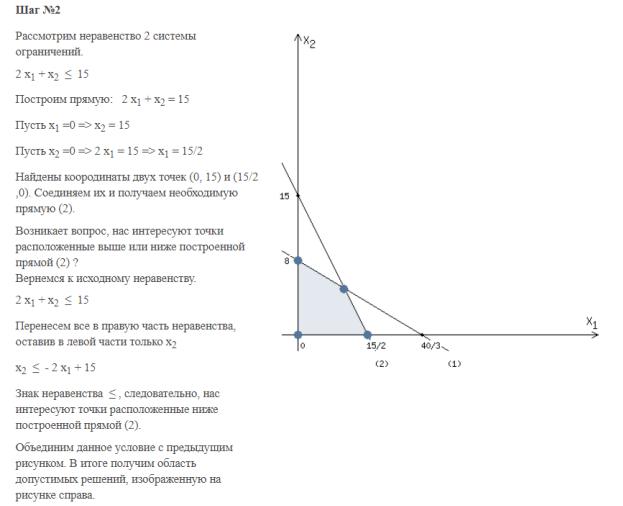
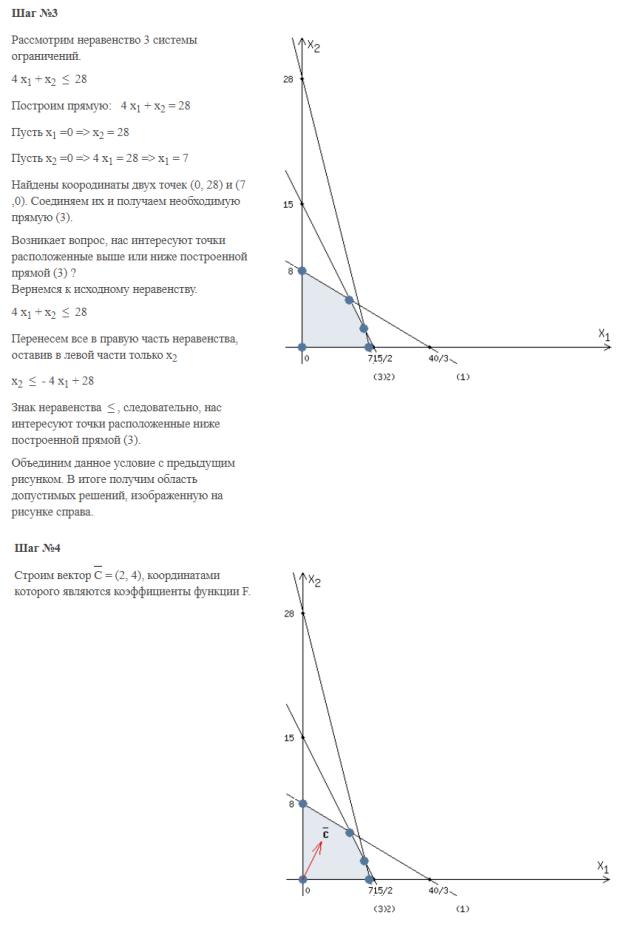


Задача 18
Завод тяжелого машиностроения производит станки двух видов 3СБШ и 6СБШ. Для данного производства используется три вида сырья: металлопрокат в объеме 77 усл.ед., трубы в объеме 78 усл.ед, чугуны в объеме 54 усл.ед. На производство одного станка вида 3СБШ расходуется 1 усл.ед. металлопроката, 4 усл.ед. труб, 4 усл.ед. чугунов. Выпуск одного станка вида 6СБШ требует затрат металлопроката в количестве 7 усл.ед, труб в количестве 5 усл.ед. и 1 усл.ед. чугунов. Прибыль завода от реализации одного станка вида 3СБШ составит 3 ден.ед., а прибыль от реализации одного станка вида 6СБШ равна 4 ден.ед. Составит план производства станков указанного вида, который приносил бы заводу наибольшую прибыль.
РЕШЕНИЕ:
1) Построим математическую модель задачи.
Представим исходные данные в виде таблицы:
|
Нормы расхода сырья на |
|
|
Вид сырья |
производство одного станка |
Запасы |
|
|
|||
|
|
сырья |
|
|
|
|
|
|
3СБШ |
6СБШ |
|
|
|
|
|
Металлопрокат, усл.ед. |
1 |
7 |
77 |
|
|
|
|
Трубы, усл.ед. |
4 |
5 |
78 |
|
|
|
|
Чугуны, усл.ед. |
4 |
1 |
54 |
|
|
|
|
Прибыль от реализации |
3 |
4 |
|
одного станка, ден.ед. |
|
||
|
|
|
|
|
|
|
|
Объектом моделирования является процесс получения максимальной прибыли дохода от реализации выпускаемых станков, а целью – оптимизация структуры и объема выпуска станков.
Задача относится к классу оптимизационных задач. Математическая модель для задач такого класса состоит в построении целевой функции, для которой надо найти экстремум, при ограничениях.
Для решения поставленной задачи введем обозначения:
х1 – количество производства станков вида 3СБШ;
х2 – количество производства станков вида 6СБШ.
Общую прибыль завода от реализации выпускаемых станков можно определить по формуле:
F(X ) 3x |
4x |
2 |
1 |
|
(ден.ед.)
Функция F называется целевой, ее следует максимизировать. Поэтому получаем:
F 3x |
4x |
2 |
max |
1 |
|
|
На целевую функцию накладываются следующие ограничения:
а) ограничение по запасу металлопроката:
х |
7х |
2 |
77 |
1 |
|
|
(усл.ед.);
б) ограничение по запасу труб:
4х |
5х |
2 |
78 |
1 |
|
|
(усл.ед.);
в) ограничение по запасу чугунов:
4х |
х |
2 |
54 |
1 |
|
|
(усл.ед.);
д) условия неотрицательности количества производства:
х |
0, |
1 |
|
х |
2 |
|
0
.
е) условия целочисленности количества производства (с учетом того, что завод производит станки):
х |
, х |
2 |
1 |
|
целые
числа
.
Математическая модель задачи: составить оптимальный план производства (х1, х2), обеспечивающий максимальную прибыль от реализации
