
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра АПУ
отчет
по практической работе №1
по дисциплине «Программирование систем реального времени»
Тема: Расчет изменения энтропии системы
Студент гр. 8391 |
|
Маликов А.А. |
Преподаватель |
|
Доцент, к.т.н. Писарев А.С. |
Санкт-Петербург
2021
Цель работы.
Расчет изменения энтропии системы при переходе от начального состояния к установившемуся.
Основные теоретические положения.
Организация и энтропия
Введем в рассмотрение понятие «состояние» элемента или системы.
Количество состояний (мощность множества состояний) может быть конечно, счётно (количество состояний измеряется дискретно, но их число бесконечно); мощности континуум (состояния изменяются непрерывно и число их бесконечно и несчетно).
Состояния можно описать через переменные состояния. Если переменные – дискретные, то количество состояний может быть либо конечным, либо счетным. Если переменные – аналоговые (непрерывные), тогда – мощности континуум.
Минимальное количество переменных, через которые может быть задано состояние, называется фазовым пространством. Изменение состояния системы отображается в фазовом пространстве фазовой траекторией.
Уравнение состояния системы:
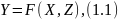
где Z – переменные состояния (вектор аналоговых или дискретных величин), Х – входные переменные, Y – выходные переменные системы.
Одной из наиболее часто используемых характеристик организации является энтропия (поворот, превращение – греч.).
Энтропия систем
Степень организации элементов в системе связывается с изменением (снижением) энтропии системы по сравнению с суммарной энтропией элементов. Понятие энтропии введено Больцманом для термодинамических систем:
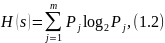
где
 -
вероятность j-го состояния (в теории
информации – события); m - возможное
число состояний (событий).
-
вероятность j-го состояния (в теории
информации – события); m - возможное
число состояний (событий).
Для расчета изменения энтропии системы через вероятности состояний очень часто используется метод Колмогорова.
Допустим, дана структурная схема (граф) состояний подсистемы S (см. рис. 1.2). Исходным состоянием системы с равной степенью вероятности может быть одно из четырех состояний, т.е.
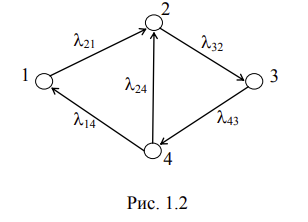

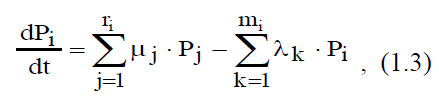 Будем
считать, что интенсивности переходов
Будем
считать, что интенсивности переходов
 заданы. Тогда можно показать, что скорости
изменения вероятности нахождения
системы в i-м состоянии определяются
как
заданы. Тогда можно показать, что скорости
изменения вероятности нахождения
системы в i-м состоянии определяются
как
Где


 число узлов графа (количество состояний);
число узлов графа (количество состояний);

 интенсивности
переходов по дугам, входящим в i-й узел;
интенсивности
переходов по дугам, входящим в i-й узел;
 – число дуг,
входящих в i-й узел;
– число дуг,
входящих в i-й узел;

 -
интенсивности переходов по дугам,
исходящим из i-го узла;
-
интенсивности переходов по дугам,
исходящим из i-го узла;
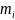 – число дуг,
выходящих из i-го узла;
– число дуг,
выходящих из i-го узла;
 и
и
 – вероятности нахождения системы в i-м
и j-м состояниях соответственно.
– вероятности нахождения системы в i-м
и j-м состояниях соответственно.
Заметим, что

Установившееся значение вероятности нахождения системы в i-м состоянии определяется из условия

Тогда для системы с n состояниями имеем систему из (n + 1) уравнений с n неизвестными:
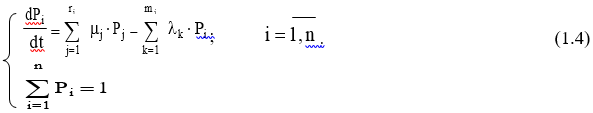
Одно из уравнений
(1.4) можно отбросить, так как оно может
быть получено из
 оставшихся.
оставшихся.
Вариант.
11 |
Исх. |
1 |
2 |
2 |
3 |
3 |
4 |
5 |
6 |
6 |
Вх. |
2 |
3 |
5 |
4 |
5 |
3 |
6 |
4 |
1 |
|
Вес |
0,9 |
0,1 |
0,8 |
0,9 |
0,2 |
0,9 |
0,5 |
0,3 |
0,9 |
Выполнение работы.
Построим граф состояний для указанного варианта:
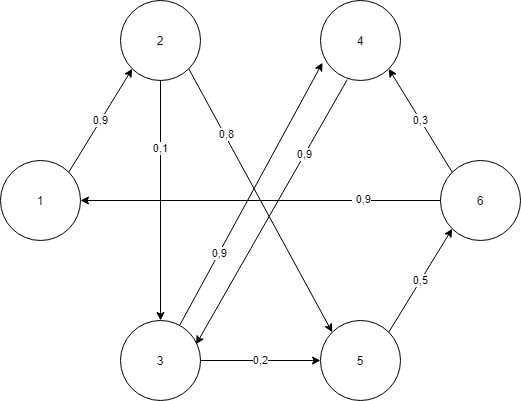
Рис. 1. Граф состояний согласно вар. 11.
Рассчитаем энтропию системы в исходном состоянии, приняв все состояния равновероятными:

Составим систему уравнений для расчета вероятностей состояний в установившемся режиме в соответствии с графом, заменив отрицательные переходы на положительные:

Исключим 6-ое уравнение из системы за ненадобностью и ради упрощения. Решим данную систему уравнений с помощью средств MATLAB:
Зададим матрицу коэффициентов.
>>A = [-0.9 0 0 0 0 0.9;
0.9 -0.9 0 0 0 0;
0 0.1 -1.1 0.9 0 0;
0 0 0.9 -0.9 0 0.3;
0 0.8 0.2 0 -0.5 0;
1 1 1 1 1 1;];
Зададим столбец свободных членов.
>>B = [0; 0; 0; 0; 0; 1;];
Проверим определитель на ненулевое значение.
>>det(A)
ans = -0.7096
Найдем корни СЛАУ методом Крамера.
>>x=inv(A)*B
x =
0.1027
0.1027
0.2055
0.2397
0.2466
0.1027
Определим энтропию системы в установившемся режиме и изменение энтропии.

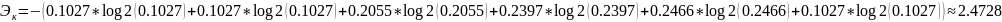

Выводы.
В ходе выполнения данной практической работы были изучены такие понятия, как переменные состояния, фазовые траектории, фазовые пространства, энтропия системы, а также рассчитаны вероятности состояний системы в установившемся режиме и изменение её энтропии. Таким образом, энтропия выступает в качестве меры беспорядка и ее снижение означает повышение уровня организации.
