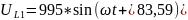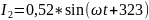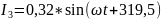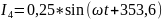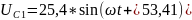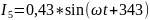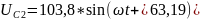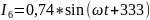3.6 Результаты анализа во временной форме

Напряжения на элементах и токи в ветвях во временной форме:

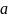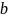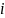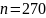Где – действительная часть числа, – мнимая часть (без ), – 90 или 270 градусов, в зависимость от того, с каким знаком переменная (если она отрицательна, то , если она положительна, то 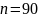. Эти значения определены по тригонометрическому кругу, т.к. переменная принимается, как ось ).

Токи ветвей:	Напряжение на элементах:

3.7 Векторная диаграмма напряжений на комплексной области путем обхода первого контура

Ниже (см.рис.5) представлены векторные диаграммы напряжений на комплексной области путём обхода первого контура .

Следуя из показаний на диаграммах, второй закон Кирхгоффа выполняется, что и требовалось доказать.

Рисунок 5 – Векторные диаграммы на комплексной области путём обхода первого контура .

На рисунке представлены векторные диаграммы напряжений на комплексной области первого контура : , 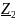и (см.рис.6).

Рисунок 6 - Векторные диаграммы напряжений , и .

4. Построение частотных характеристик входного сопротивления и передаточной функции

Преобразуем исходную схему в такую, где отсутствуют источники тока (см.схем.8).

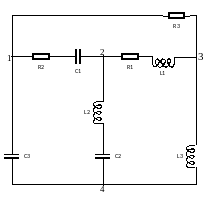
Схема 8 – Схема без источников тока.

Упрощаем схему из «звезды» в треугольник (см.схем.9) в 3 шагах.

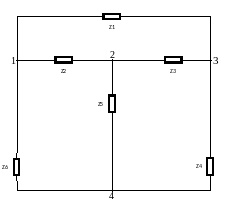
Схема 9 – Преобразование в треугольник Шаг-1.

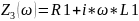
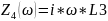
Следующий шаг преобразования из «звезды» в треугольник (см.схема.10).

Схема 10 – Преобразование в треугольник Шаг-2.

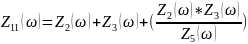
Схема 11 – Преобразование в треугольник Шаг-3.

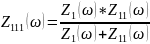
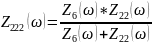
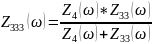
Ниже указаны формулы и схема для построения необходимых графиков зависимостей с помощью программ Mathcad и Microcap (см.схем.12).

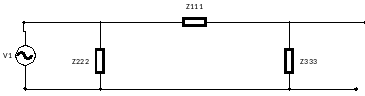Схема 12 – Схема, используемая для расчетов.

Ниже показаны формулы, используемые для расчетов.

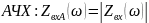
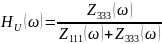
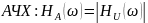
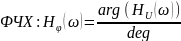
На рисунке показаны графики АЧХ и ФЧХ от , принятым от 10 до 500 (см.рис.7).

Рисунок 7 – Графики зависимости от .

На рисунке показаны графики АЧХ и ФЧХ от , принятой от 10 до 500 (см.рис.8).

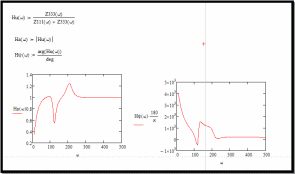
Рисунок 8 - Графики зависимости от

На рисунке показаны сопоставления вышеописанных графиков АЧХ и ФЧХ для и соответственно (см.рис.9).

Рисунок 9 – Графики АЧХ и ФЧХ для и на одной плоскости.

На рисунке показаны графики АЧХ и ФЧХ, нарисованные в программе Microcap (см.рис.10).

Рисунок 10 – Графики АЧХ и ФЧХ в программе Microcap.

На рисунке показаны графики АЧХ и ФЧХ, нарисованные в программе Microcap, но на одной координатной плоскости (см.рис.11).

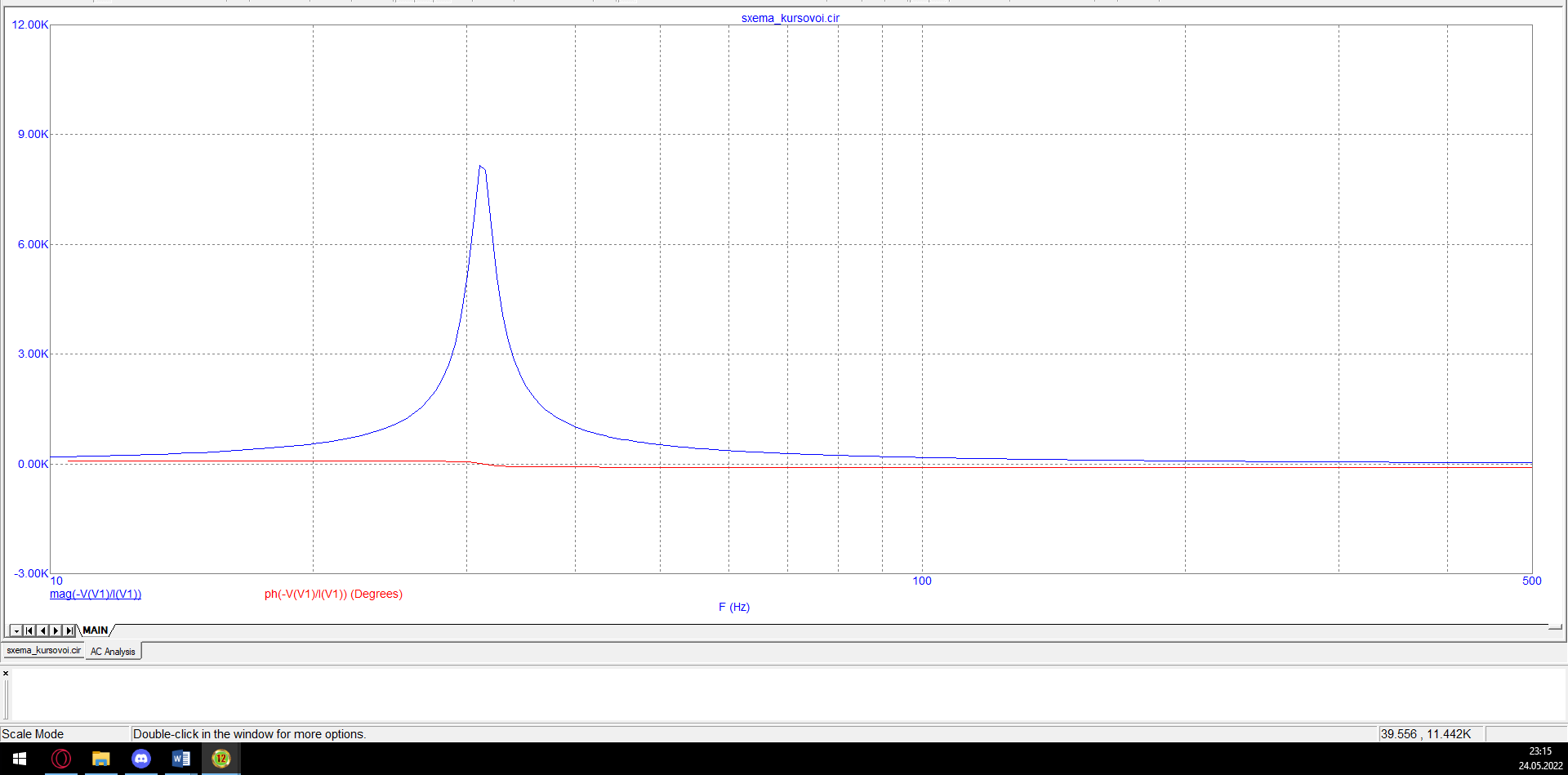
Рисунок 11 – Графики АЧХ и ФЧХ в программе Microcap на одной координатной плоскости.

Вывод

Был проведён анализ электрической цепи: найдены напряжения на катушках индуктивности, конденсаторы, составлены эквивалентные схемы при законах коммутации, составлены матрицы сопротивлений в вещественном и комплексном виде, найдены значения токов и напряжений на элементах в комплексной, экспоненциальной и временной формах, построены графики в программах Mathcad и Microcap, доказаны первый и второй законы Кирхгоффа и проведены преобразования схем. Проведена работа в Mathcad и Micro-cup. Найдены фчх, ачх передаточной функции и входного сопротивления.