лабы / Laba_varik12_7

СОДЕРЖАНИЕ

1)ЦЕЛЬ РАБОТЫ

2)ФОРМУЛИРОВКА ЗАДАЧИ №12

3)ФОРМАЛИЗАЦИЯ ЗАДАНИЯ

4)РАЗРАБОТКА АЛГОРИТМОВ РЕШЕНИЯ ЗАДАЧИ

5)РАЗРАБОТКА ПРОГРАММНОГО КОДА ПРОЕКТА

6)РЕЗУЛЬТАТЫ ВЫПОЛНЕНИЯ ПРОГРАММЫ

7)ДОКАЗАТЕЛЬСТВО ПРАВИЛЬНОСТИ РАБОТЫ ПРОГРАММЫ

1

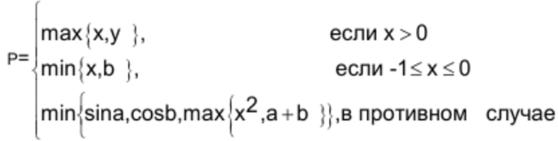
ЦЕЛЬ РАБОТЫ

1)Разработать и написать консольный проект, содержащий два алгоритма, которые вычисляют выражение. Первый с помощью базовых алгоритмов нахождения минимального и максимального, а второй с помощью вспомогательных функций.

2)Оформить отчет по работе.

ФОРМУЛИРОВКА ЗАДАЧИ №12

Рисунок 1 – формулировка задачи №12

ФОРМАЛИЗАЦИЯ ЗАДАНИЯ

Чтобы решить данную задачу требуется написать два алгоритма, отличающихся тем, что один из них будет использовать базовые алгоритмы нахождения максимума и минимума, а другой для этой задачи будет использовать созданные нами функции max и min, которые значительно упрощают запись кода. Для переменных, вводимых пользователем, а также выдающих результат, будем использовать тип double.

2

РАЗРАБОТКА АЛГОРИТМОВ РЕШЕНИЯ ЗАДАЧИ

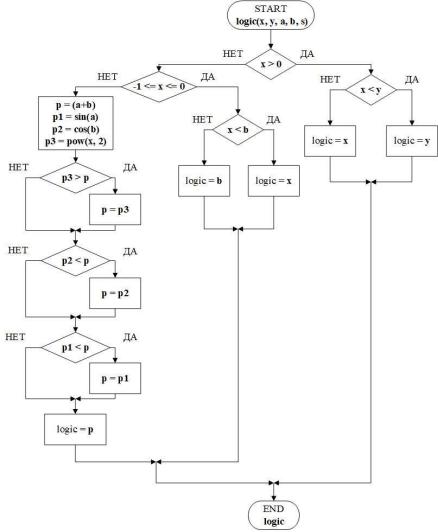
Первый алгоритм – алгоритм решения задачи, использующий вложенные разветвления с базовыми алгоритмами нахождения наибольшего и наименьшего значений без использования библиотечных функций. (см. рис. 2)

Рисунок 2 – схема алгоритма logic

Для второго алгоритма решения задачи потребуются библиотечные функции нахождения минимального и

максимального значения. (см. рис. 3)

3

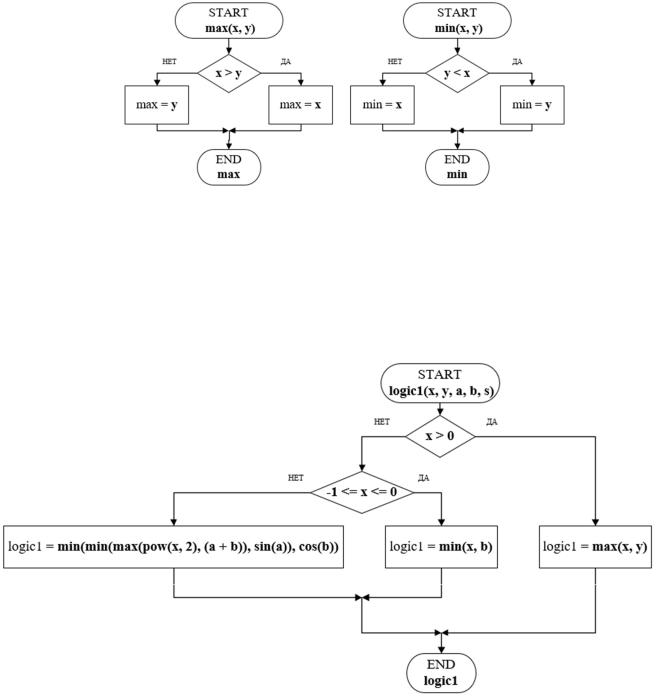
Рисунок 3 – алгоритмы для нахождения максимума и минимума

Второй алгоритм - алгоритм, использующий для решения задачи заданные нами библиотечные функции, находящие наибольшее и наименьшее значения. (см. рис. 4)

Рисунок 4 – схема алгоритма logic1

Для основной функции мы будем использовать оператор switch для выбора пользователем варианта алгоритма решения. (см. рис. 5)

4

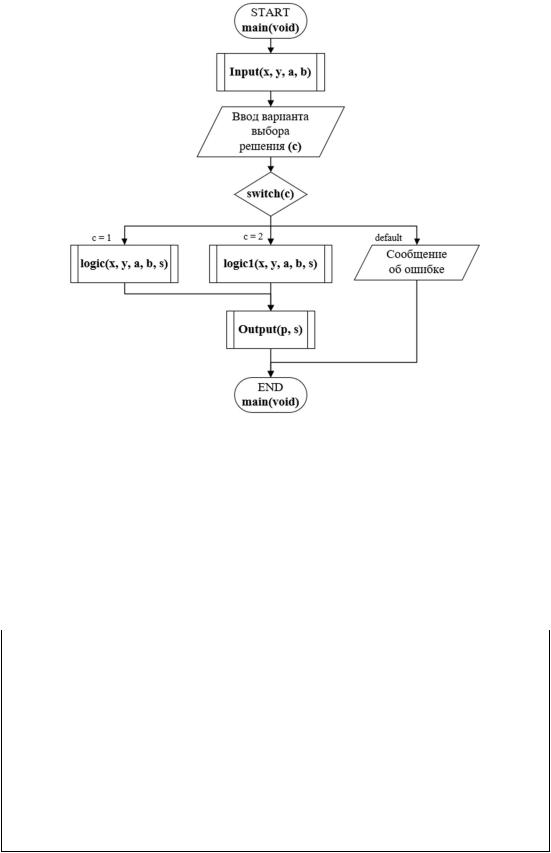
Рисунок 5 – схема главной процедуры main

РАЗРАБОТКА ПРОГРАММНОГО КОДА ПРОЕКТА

Напишем код для библиотеки “minmax.h” с двумя функциями. (см. рис. 6)

1.#pragma once

2.double min(double x, double y)

3.{

4.double f;

5.if (x > y) f = y;

6.else f = x;

7.return f;

8.}

9.double max(double x, double y)

10.{

11.double f;

12.if (x > y) f = x;

13.else f = y;

14.return f;

15.}

Рисунок 6 – код библиотеки “minmax.h”

5

Теперь напишем код главной функции main и в отдельный файл код функций Input и Output. (см. рис. 7, 8)

1.#include <iostream>

2.#include "inpoutp.h"

3.#include "logic.h"

4.#include "minmax.h"

6.using namespace std;

7.void main(void)

8.{

9.double x, y, a, b, p;

10.int s, c;

11.Input(x, y, a, b);

12.cout << "Каким способом решать задачу?\n";

13.cout << "1 - с вложенными разветвлениями";

14.cout << " без дополнительных функций max min\n";

15.cout << "2 - со своими фунцкиями max и min\n" << "Способ - ";

16.cin >> c;

17.switch (c)

18.{

19.case 1:

20.p = logic(x, y, a, b, s);

21.break;

22.case 2:

23.p = logic1(x, y, a, b, s);

24.break;

25.default:

26.cout << "Такого способа решения нет!";

27.break;

28.}

29.Output(p, s);

30.}

Рисунок 7 – код файла с исходным кодом “lab7.2.cpp”

1.#pragma once

2.#include <iostream>

4.using namespace std;

5.void Input(double& x, double& y, double& a, double& b)

6.{

7.setlocale(LC_ALL, "rus");

8.cout << "Введите пременную x = ";

9.cin >> x;

10.cout << "\nВведите пременную y = ";

11.cin >> y;

12.cout << "\nВведите пременную a = ";

13.cin >> a;

14.cout << "\nВведите пременную b = ";

15.cin >> b;

16.}

17.void Output(double p, int& s)

18.{

19.setlocale(LC_ALL, "rus");

20.cout << "Ответ = " << p << endl;

21.cout << "Номер ветки разветвления - " << s;

22.}

Рисунок 8 – код библиотеки “inpoutp.h”

6

И наконец, в библиотеку под названием “logic.h” напишем программный код функций logic и logic1, выполняющих все логические операции и вычисления. (см. рис. 9, 10)

1.double logic(double x, double y, double a, double b, int& s)

2.{

3.double p;

4.if (x > 0)

5.{

6.if (x < y)

7.p = y;

8.else

9.p = x;

10.s = 1;

11.}

12.else

13.if (((-1 < x) && (x < 0)) || (x == -1) || (x == 0))

14.{

15.if (x > b)

17.else

19.s = 2;

20.}

21.else

22.if (pow(x, 2) > (a + b))

23.{

33.}

34.else

35.{

44.}

45.return p;

46.}

Рисунок 9 – код функции logic

7

1.double logic1(double x, double y, double a, double b, int& s)

2.{

3.double p;

4.if (x > 0)

5.{

6.p = max(x, y);

7.s = 1;

8.}

9.else

10.if (((-1 < x) && (x < 0)) || (x == -1) || (x == 0))

11.{

12.p = min(x, b);

13.s = 2;

14.}

15.else

16.{

17.p = min(min(max(pow(x, 2), (a + b)), sin(a)), cos(b));

18.s = 3;

19.}

20.return p;

21.}

Рисунок 10 – код функции logic1

РЕЗУЛЬТАТ ВЫПОЛНЕНИЯ ПРОГРАММЫ

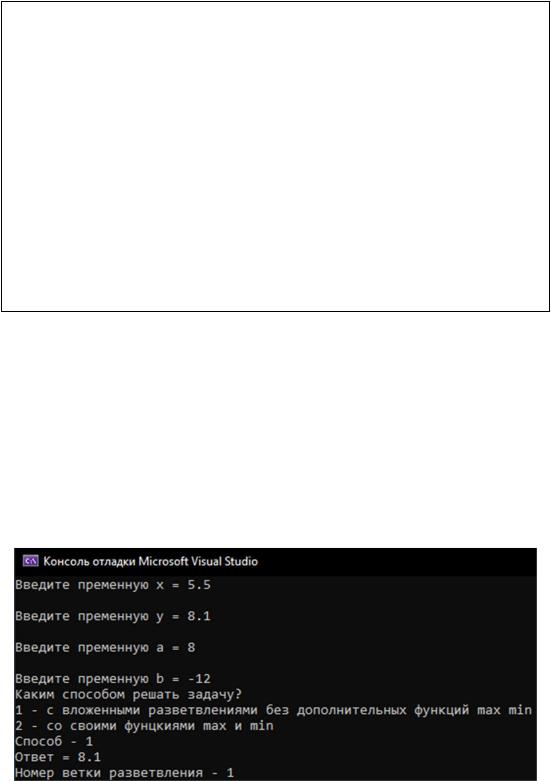
Возьмем дважды четыре числа. Пусть для 1 способа решения переменные будут такие: x1 = 5.5; y1 = 8.1; a1 = 8; b1 = 12.

Тогда результат будет такой – (см. рис. 11)

Рисунок 11 – результат работы программы при использовании 1- го способа решения задачи

8

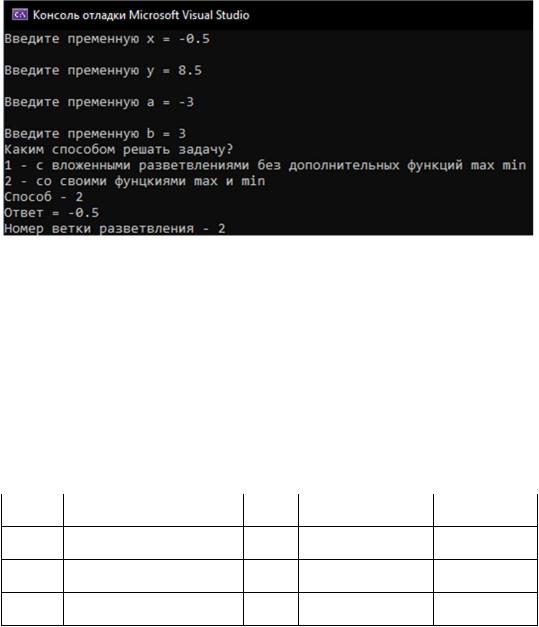
Пусть для 2-го способа решения переменные будут такие: x2 = -0.5; y2 = 8.5; a2 = -3; b2 = 3.

Тогда результат будет такой – (см. рис. 12)

Рисунок 12 – результат работы программы при использовании 2- го способа решения задачи

ДОКАЗАТЕЛЬСТВО ПРАВИЛЬНОСТИ РАБОТЫ ПРОГРАММЫ

Таблица 1 – доказательство правильности работы программы

При тестовых данных результаты ручного расчета и вычисления компьютера совпадают.

9