книги / 949

21

=qA2 (0,125 −0,0625)= 0,0625 qA2 .

3.Из условия прочности в опасном сечении определяем несущую способность обрешётины, т. е. величину расчетной нагрузки qрасч .

=1,508 кН/м.

Второй способ решения

4. Строим эпюру изгибающих моментов в силовой плоскости (рис. 2.8).

Рис. 2.8

22

Изгибающие моменты в плоскостях осей x и y сечения обрешётины:

M x = Mu cosα, M y = Mu sin α.

Из условия прочности в опасном сечении рассчитываем несущую способность обрешётины, т. е. определяем величину расчетной нагрузки qрасч :

или

откуда

5. Определяем полный прогиб в середине пролета. Используем известную зависимость прогиба в середине пролета для заданного нагруже-

ния [9, табл. 27. С. 297]:

f = 5qA4 . 384EJ

Тогда полный прогиб для заданного косого изгиба обрешётины определяется как геометрическая сумма прогибов в плоскостях осей x и y :

= 83777,78108 0,999978 =83775,94 10−8 м= 0,84 мм.

Ответ: наибольшая допускаемая величина нагрузки составила qрасч =1,5 кН/м, а полный прогиб обрешётины в середине её пролета –

f = 0,84 мм.

Пример 2.3

Деревянная балка прямоугольного поперечного сечения, шарнирно опертая по концам (шаровые шарниры), нагружена в середине пролета сосредоточенной силой F =8 кН (рис. 2.9, а, 2.10, а). Плоскость действия

нагрузки составляет угол ϕ =12D с вертикальной плоскостью, проходящей через ось балки (рис. 2.9, а). Определить нормальные напряжения в точках A , B , C и D сечения; построить эпюры напряжений по сторонам сечения балки при величине расчетного сопротивления R =10 МПа; A =1,5 м; b =12 см; h = 20 см. Проверить прочность балки.

Рис. 2.9

Решение

1. Определяемосновныегеометрическиехарактеристикисечениябалки:

• осевые моменты инерции:

2. Рассчитываем внутренние изгибающие моменты в сечении балки и строим их эпюры в вертикальной (рис. 2.10, б) и горизонтальной (рис. 2.10, в) плоскостях.

Из построенных эпюр очевидно, что опасным сечением является сечение в середине пролета балки. При этом вертикальная проекция приложенной силы Fy растягивает нижние волокна балки, а верхние сжимает.

Горизонтальная проекция силы Fx растягивает правые волокна, а левые – сжимает (рис. 2.9, б).

а

б

в

Рис. 2.10

3. Определяем нормальные напряжения в угловых точках опасного сечения.

Формула нормальных напряжений для любой точки сечения имеет вид

25

или

= ±0,0368 y ±0,0195 x .

Первое слагаемое в полученном выражении соответствует изгибающему моменту в вертикальной плоскости M x , второе – моменту в горизонтальной плоскости M y . Знаки слагаемых принимаем в зависимости от

действия соответствующего изгибающего момента на рассматриваемом волокне – растяжение « +», сжатие «–» (рис. 2.9, б, 2.11). Координаты точки x и y принимаем c положительным знаком вне зависимости от поло-

жения рассматриваемой точки относительно осей Ox и Oy .

Рис. 2.11

26

Напряжение в точке A ( xA = −6 см; yA =10 см):

σA = −0,0368 10 +0,0195 6 = −0,251 кН/см2 = −2,51 МПа.

Напряжение в точке B ( xB = 6 см; y B =10 см):

σB = −0,0368 10 −0,0195 6 = −0,485 кН/см2 = −4,85 МПа.

Напряжение в точке C ( xC = 6 см; yC = −10 см):

σC = 0,0368 10 −0,0195 6 = 0,251 кН/см2 = −2,51 МПа.

Напряжение в точке D ( xC = −6 см; yC = −10 см):

σC = 0,0368 10 +0,0195 6 = 0,485 кН/см2 = 4,85 МПа.

Строим эпюру нормальных напряжений σ в точках сечения балки (рис. 2.11) и в аксонометрии (рис. 2.12).

4. Проверяем прочность балки.

В опасной точке поперечного сечения

σmax = σD = 4,85 МПа< R =10 МПа;

так как условие выполняется, прочность балки обеспечена.

Рис. 2.12

27

Из рис. 2.12 видно, что через точки пересечения эпюры напряжений поперечного сечения проходит нейтральная линия (II и IV четверти сечения и центр тяжести).

Ответ. Напряжения в характерных точках сечения составляют:

σA = −2,51 МПа; σB = −4,85 МПа; σC = 4,85 МПа; σD = 2,51 МПа. Проч-

ность балки в опасных точках обеспечена.

3. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ (СЖАТИЕ) СТЕРЖНЯ

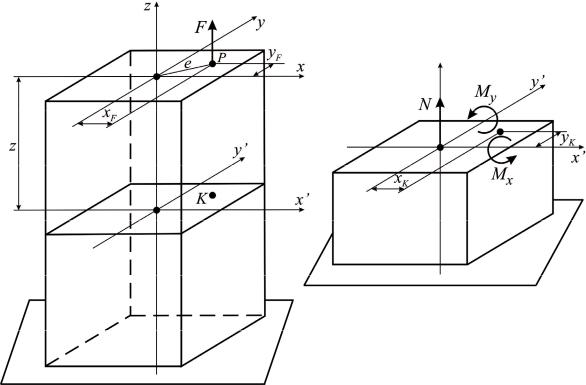
Этот вид нагружения прямолинейного бруса возникает тогда, когда линия действия внешней силы параллельна оси стержня, а точка ее приложения не совпадает с центром тяжести его сечения.

В общем случае внецентренное растяжение (сжатие) можно рас-

сматривать как комбинацию чистого косого изгиба и центрального растяжения (сжатия). На рис. 3.1, а представлен случай внецентренного растяжения бруса. Точка приложения силы F называется полюсом, расстояние от центра тяжести сечения до полюса − эксцентриситетом ( e ).

Рис. 3.1

28

Из рис. 3.1, а видно, что N = +F ; M x = F yF ; M y = F xF . Внутренние силовые факторы не зависят от z , и их действие распро-

страняется на любое поперечное сечение. Напряжение в точке K, находящейся в I четверти, определяется по формуле

σK = σK (N )+σK (M x )+σK (M y );

где Jx , J y − главные центральные моменты инерции; N, M x , M y − внут-

ренние усилия.

xF , yF и xK , yK − координаты полюса и исследуемой точки K; они

положительны, так как находятся в I четверти (рис. 3.1, б). От каждого внутреннего силового фактора σ будут растягивающими, поэтому все слагаемые входят в формулу σK с положительными знаками. При определе-

Знак «+» или «−» перед формулой зависит от направления силы F и от того, растяжение или сжатие создает эта сила. Координаты полюса и исследуемых точек ставятся с соответствующими знаками в системе координат главных центральных осей.

Положение нейтральной линии определяется из условия, что напря-

29

Из аналитической геометрии известно уравнение прямой линии в отрезках:

где

Выражения (3.2) называются уравнением нейтральной линии в от-

резках. Из него видно, что нейтральная линия при внецентренном растяжении (сжатии) представляет собой прямую, не проходящую через центр тяжести сечения и отсекающую от осей координат отрезки ax и ay со сто-

роны, противоположной полюсу. Нейтральная линия делит плоскость сечения бруса на две зоны: растянутую и сжатую. Для конструкций, выполненных из хрупкого материала, наличие этих двух зон нежелательно, так как материал сопротивляется растяжению хуже, чем сжатию.

Наибольшие напряжения будут в точках, наиболее удаленных от нейтральной линии сечения. Для этих точек должны выполняться условия прочности:

соответственно.

Если полюс силы лежит на одной из главных осей инерции сечения, то перед нами плоский случай внецентренного растяжения (сжатия).

Из условий прочности (3.3) можно выполнить любой расчет на прочность: проверочный, проектировочный, и вычислить несущую способность.

30

На основе формул (3.2) можно определить форму и размеры ядра сечения. Ядром сечения называется область вокруг центра тяжести, обладаю-

щая таким свойством: если приложенная нагрузка расположена в области ядра, то нормальные напряжения во всех точках сечения имеют один знак, а нейтральная линия либо касается поперечного сечения, либо выходит за его пределы. И тогда напряжения будут одного знака, образуя только одну зону − растяжения или сжатия, в зависимости от приложенной нагрузки.

Положение ядра сечения важно знать для конструкций, выполненных из хрупкого материала, который сопротивляется растяжению и сжатию неодинаково.

Примеры расчета

Пример 3.1

Для чугунного короткого стержня заданного поперечного сечения, сжимаемого продольной силой F , приложенной параллельно оси стержня в точке K (рис. 3.2), требуется:

• установить положение главных центральных осей инерции сечения (положение центра тяжести т. C ) и вычислить главные моменты ( Jx , J y ) и главные радиусы инерции сечения (ix , iy );

•определить положение нейтральной линии и показать ее на чертеже поперечного сечения стержня;

•определить по чертежу координаты точек сечения, наиболее удаленных от нейтральной линии (опасные точки);

•вычислить наибольшие растягивающие и сжимающие напряжения, выразив их через силу F и параметры сечения;

•исходя из условия прочности, найти величину нагрузки F , если

расчетные сопротивления материала растяжению и сжатию R t =55 МПа, R c =160 МПа; коэффициент условий работы γc =1;

• построить эпюру нормальных напряжений от полученной нагрузки Fн , коэффициент надёжности по нагрузке γf =1,1;

• определить размеры ядра сечения и изобразить его на чертеже поперечного сечения.

Исходные данные: b =20 см; xF = b =20 см.