
книги / 830
.pdf
О пределах упругости и прочности горных пород
стояния характеризуется отношением минимального и максимального главных напряжений c =σ1 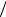 σ3 . Как это часто принимается в теорети-
σ3 . Как это часто принимается в теорети-
ческих расчетах, предел упругости будем отождествлять с пределом пропорциональности и пределом текучести. Пределы прочности определим, используя критерий Мора.
Следуя Мору [4], будем считать, что первоначальные локальные скольжения возникают на площадке, на которой касательное τν и нор-
мальное σν напряжения связаны следующим соотношением:
τν =S0 −µσν , |
(1) |
где S0 и µ – параметры материала; ν – нормаль к рассматриваемой
площадке. Правая часть выражения представляет собой сопротивление скольжению (сдвигу).
Нормальное и касательное напряжения в плоскости, повернутой относительно площадки действия максимального касательного напряжения на угол β, определяются по формулам
|
|
σβ =σ0 |
+Тsin2β, |
|
(2) |
||
|
|
τβ =Тcos2β, |
|
|
|||
|
|
|
|
|
|||
где σ0 – среднее напряжение; T |
– максимальное касательное напря- |
||||||
жение, т.е. |
|
|
|
|
|
|
|
σ = 1 |
(σ +σ ) , T = 1 |
(σ −σ ) . |
(3) |
||||
0 |
2 |
1 |
3 |
2 |
1 |
3 |
|
Согласно определению сопротивление сдвигу ( Sβ ) выражается в дан- |
|||||||
ном контексте следующим образом: |
|
|
|
||||
|
Sβ =S0 −µ(σ0 +T sin2β) . |
|
(4) |
||||
При первом скольжении |
|
касательные |
к кривым |
Sβ =Sβ (β) |
|||
и τβ =τβ (β) совпадут, т.е. касательное напряжение τβ (β) достигает значения сопротивления сдвигу в направлении этого скольжения:
dSβ |
= |
dτβ |
при β=β , |
(5) |
|
|
|||
dβ |
|
dβ |
0 |
|
|
|
|
||
|
|
|
|
111 |

Б.А. Рычков, Н.М. Комарцов, Т.А. Лужанская
где β0 – угол, определяющий направление первого скольжения, отсчи-
тываемый от направления действия максимального касательного напряжения T .
Из (5), учитывая (1), (2), (3) и (4), вытекает, что |
|
µ=tg2β0 . |
(6) |
Таким образом, величина угла β0 определяется параметром µ,
величину которого будем считать зависящей от вида напряженного состояния.
Естественно считать, что при пропорциональном нагружении в площадках, отмечаемых углом β0 , интенсивность скольжений с рос-
том уровня напряжений наибольшая, и именно по этим площадкам происходит срез при разрушении образца.
Согласно опытным данным [5], начиная с напряженного состояния c =1 3 и выше, угол β0 =0 , т.е. при данном напряженном состоя-
3 и выше, угол β0 =0 , т.е. при данном напряженном состоя-
нии срез происходит по плоскости максимального касательного напряжения (Т), и горные породы деформируются как пластичный материал. Тогда при c =1 3 из соотношений (2) и (3) вытекает, что
3 из соотношений (2) и (3) вытекает, что
|
|
|
|
|
|
|
|
|
|
σβ0 |
=2 . |
|
|
(7) |
||
|
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
При с, отличных от 1 3, это отношение выглядит следующим об- |
||||||||||||||||
разом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σβ |
|
(1+c)+(1−c)sin2β |
|
|||||||||
|
|
|
|
|
0 |
= |
|
|
|
|
|
0 =k (c). |
(8) |
|||
|
|
|
|
τ |
|
|
1−c |
cos2β |
||||||||
|
|
|
|
β0 |
|
|
( |
) |
|
0 |
|
|
|
|||
Предположим, что отношение (8) линейно изменяется от значе- |
||||||||||||||||
0 |
=k |
( ) |
( |
|
) |
=2 . |
Исходя из геометрических построений в |
|||||||||
ния k |
0 |
до k 1 3 |
||||||||||||||
круге Мора на сжатие (рис. 1), величина k0 |
определяется по формуле |
|||||||||||||||
|
|
|
|
|
|
|
|
k |
= |
1+cos2α0 |
, |
|
(9) |
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
0 |
|
|
sin2α0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где угол α0 =45°−β0 определяется экспериментально.
112

О пределах упругости и прочности горных пород
Рис. 1. Круг Мора при одноосном сжатии
На этом рисунке Оц – центр круга Мора при одноосном сжатии; σ0 ,τ0 – координаты точки касания огибающей круга на одноосное сжатие; σc – предел прочности при одноосном сжатии; α0 – угол среза.
Из приведенного выше предположения, что α→45° при с=1 3 получим, что в плоскости среза соотношение между нормальным и касательным напряжениями все время изменяется с изменением вида напряженного состояния. Это обстоятельство можно учесть, если для коэффициента k ввести интерполяционную формулу:
3 получим, что в плоскости среза соотношение между нормальным и касательным напряжениями все время изменяется с изменением вида напряженного состояния. Это обстоятельство можно учесть, если для коэффициента k ввести интерполяционную формулу:
k =k(c) =113 ckn +(13−c)k0 ,
где kn равно значению, получаемому для предельного напряженного состояния ( с=1 3 ), при котором еще справедлив критерий Кулона–
3 ), при котором еще справедлив критерий Кулона–
Мора.
Из соотношения (8), учитывая формулы (2) и (3), можно определить угол среза β0 при произвольном с:
|
− 1+c |
) |
+k 1+k2 |
1−c 2 |
− 1+c 2 |
|
|||
sin2β = |
( |
( |
|
)( ) |
( ) |
. |
(10) |
||
|
|
( |
)( |
|
) |
|
|||
0 |
|
|
|
|
|
|
|||
|
|
1−c |
1+k2 |
|
|
|
|
||
Учитывая (2),(3) и (7), условие (1) можно представить в следующем виде:
113

Б.А. Рычков, Н.М. Комарцов, Т.А. Лужанская
s |
s |
(с)= |
|
|
2S0 |
|
|
|
σ1 |
=σ1 |
|
|
|
, |
(11) |
||
1−c |
)( |
cos2β +k sin2β |
||||||
|
|
( |
0 |
0 ) |
|
|
||
где σ1s – предел прочности при произвольном напряженном состоянии для c ≤1 3.
3.
Величина S0 определяется из сопоставления с экспериментальными данными. Подобно аналогичному методу [5] выражения пределов прочности, S0 представляется в следующем виде:
S0 =S00 exp(ξc +ηc2 ), |
(12) |
где ξ и η в общем случае определяются [6] по экспериментальным данным для пределов прочности при каких-либо двух видах напряженного состояния.
При c =0 параметр S0 должен быть равен пределу прочности на одноосное сжатие σс . Согласно этому условию и учитывая (11) и (12), получим
S0 |
= 1 |
σ |
cos2β0 |
+k |
sin2β0 |
β0 |
=β |
|
|
, k =k |
|
. |
|
|
|||||||||||
0 |
2 |
c ( |
0 |
0 |
0 ) |
( 0 |
0 |
|
c=0 |
0 |
|
c=0 ) |
|
|
Входящие в выражение для S0 параметры ξ и η можно опреде-
лить в первом приближении, используя только эксперимент на одноосное сжатие. Для этого вначале надо рассмотреть построение огибающей к кругам Мора.
Уравнение кругов Мора можно представить в виде [6]
ϕ(σ,τ,с) =σ2 +τ2 −(1+c)σ σ+cσ2 |
=0, |
(13) |
|
1 |
1 |
|
|
где в качестве параметра данного семейства кругов фигурирует с. Согласно известной теореме [7] огибающая семейства вида (13)
должна также удовлетворять уравнению
или |
ϕс(σ,τ,с) =0 |
( ϕс =∂ϕ/ ∂с) |
|
(14) |
||
|
|
|
|
|
|
|
ϕ (σ,τ,с) =−(σ ) (1+c)σ−σ σ+σ2 |
+2σ c(σ ) =0. |
(15) |
||||
с |
1 c |
1 |
1 |
1 1 |
c |
|
Из системы уравнений (11) и (15) определяется совокупность точек ( σ,τ ) данной огибающей:
114

О пределах упругости и прочности горных пород
σ= |
σs [σs |
+2c(σs ) ] |
, |
τ= |
|
(1−c)σs |
[σs |
+c(σs ) ](σs ) . |
(16) |
|||
1 |
1 |
1 c |
|
1 |
||||||||
σs |
+(1+c)(σs ) |
|||||||||||
|
σs |
+(1+c)(σs ) |
|
|
1 |
1 c |
1 c |
|
||||
|
1 |
|
1 c |
|
|
1 |
1 c |
|
|
|
|
|
Используя (11), найдем |
|
|
|
|
|
|
|
|||||
|
|
|
(σs ) =σs R(c), |
|
|
|
|
|
|
(17) |
||||||||
где |
|
|
|
|
1 c |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k −tg2β0 )(sin2β0 )c +kc sin2β0 |
|
|
|
|
||||||||||
|
R(c) =ξ+2cη+ |
1 |
|
− |
. |
|
(18) |
|||||||||||
|
1−c |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
cos2β +k sin2β |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
||||
Сопоставляя выражения (16) и (17), получим |
|
|
|
|
|
|||||||||||||
|
|
σ |
|
|
1+2cR |
|
|
|
|
|
|
|
(19) |
|||||
|
|
τ = |
|
(1−c) (1+cR)R . |
|
|
|
|
|
|
|
|
||||||
В случае одноосного сжатия ( с = 0 ) из (19) имеем |
|
|
|
|
|
|||||||||||||
|
|
R =R(0) =1 (σ0 / τ0 )2 , |
|
|
|
|
|
|
(20) |
|||||||||
где |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ0 / τ0 =(σ/ τ) |
|
c=0 . |
|
|
|
|
|
|
(21) |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Из (17), учитывая (11) и (18), при с = 0 получим выражение для |
||||||||||||||||||
параметра ξ : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(sin2β0 )c (k −tg2β0 )+kc sin2β0 |
|
|
|
|
|
∂ |
|
|
|
∂ |
|||||||
ξ=R+ |
|
|
|
|
|
((sin2β0 )c |
= |
|
sin2β0 |
; kc |
= |
|
k(c)). |
|||||
cos2β +ksin2β |
|
|
|
∂c |
∂c |
|||||||||||||
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Второе условие (для определения параметра η) получим, используя свойства огибающей к кругам Мора.
Координаты точки касания огибающей круга на одноосное сжатие (σ0 ,τ0 ) определяется двумя методами.
1. Рассмотрим геометрическое построение (см. рис. 1).
При известном экспериментальном значении угла среза α0 и пределе прочности на сжатие σc с помощью тригонометрических соотношений из круга Мора на сжатие определяются σ0 ,τ0 , что дает
σ0 / τ0 = |
1−cos2α |
(22) |
||
|
0 |
. |
||
sin2α |
|
|||
|
0 |
|
|
|
115

Б.А. Рычков, Н.М. Комарцов, Т.А. Лужанская
2. Выразим отношение σ0 ,τ0 как функцию от истинной пористости (Р) ряда горных пород [8]:
σ0 ,τ0 = f (P).
Предварительно отношение σ0 ,τ0 для каждой конкретной породы определяется методами, изложенными в [9]:
σ0 ,τ0 = |
2σс σp |
|
, |
1+(σ σ |
)2 |
||
|
с p |
|
|
где σp – предел прочности при растяжении.
При известных данных пористости горных пород можно получить графическую зависимость σ0  τ0 − f (P) , при аппроксимации которой получаем аналитическое выражение вида
τ0 − f (P) , при аппроксимации которой получаем аналитическое выражение вида
σ0  τ0 =a +bln P ,
τ0 =a +bln P ,
где a и b имеют определенные значения для конкретных горных пород. Определив тем или иным способом величину σ0 / τ0 , условие для параметра η, входящего в формулу (12), получим следующим образом. Максимальное касательное напряжение при переходе за указанное выше предельное состояние cn (т.е. при c > cn ) остается постоян-
ным. Иначе говоря,
|
∂ |
τ |
|
|
|
|
=0. |
|
|
(23) |
|||
|
|
|
|
||||||||||
|
∂c |
|
max |
c>c |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
Из этого равенства вытекает |
|
|
|
|
|
|
|
|
|
|
|
||
(σs ) =σs |
|
1 |
|
|
|
( c ≥ c |
n |
). |
(24) |
||||
1−c |
|||||||||||||
1 c |
1 |
|
|
|
|||||||||
Для большинства горных пород, как известно, |
cn =1/ 3 . При этом |
||||||||||||
и угол β0 с ростом c не изменяется, т.е. |
|
|
|
||||||||||
(sin2β0 )c |
|
с≥1/3 =0. |
|
|
(25) |
||||||||
|
|
|
|||||||||||
|
|
|
|
||||||||||
Таким образом, из условия (24), с учетом (17) и (18), при с =1 3 получаем выражение для параметра η:
3 получаем выражение для параметра η:
116

О пределах упругости и прочности горных пород
η=−32 ξ.
Графики зависимостей расчетных (сплошная линия) и полученных А.Н. Ставрогиным экспериментально (штриховая линия) значений пределов прочности приведены для некоторых горных пород в виде предельных кругов Мора и огибающих к этим кругам на рис. 2.
а
б
в
Рис. 2. Предельные круги Мора и огибающие к ним для талькохлорита (а); мрамора-II (б); кварцевого диорита Д-2 (в)
117

Б.А. Рычков, Н.М. Комарцов, Т.А. Лужанская
Примечание. Координаты огибающих, полученные А.Н. Ставрогиным, построены согласно прил. 5 [5]. Каким образом вычислены эти координаты в монографии [5], не указано. Возможно, в данном приложении имеются некоторые ошибки (опечатки), что наглядно проявилось в изображении соответствующей огибающей для кварцевого диорита Д-2.
Аналогично можно определить предел упругости при произвольном напряженном состоянии, заменив во всех представленных выше соотношениях пределы прочности на соответствующие пределы упругости для рассматриваемых горных пород.
Особое место занимает вопрос определения предела упругости горных пород при одноосном сжатии. Кроме того, необходимо установить, к каким материалам следует их отнести: к изотропным или анизотропным.
Как показано в [1], для многих горных пород приемлемо предположение об ортотропной симметрии в исходном состоянии.
Закон Гука для ортотропного материала представляется в виде
е = |
|
1 |
σ − |
ν12 σ − |
ν13 σ , |
|||||||||
|
|
|||||||||||||
1 |
Е |
1 |
Е |
2 |
Е |
3 |
||||||||
|
|
1 |
|
|
|
|
2 |
|
|
|
3 |
|
|
|
е =− |
ν21 |
σ + |
1 |
|
σ − |
ν23 |
σ , |
|||||||
Е |
|
Е |
||||||||||||
2 |
|
Е |
1 |
|
|
2 |
|
|
3 |
|||||
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
||
е =− |
ν31 |
σ − |
|
ν32 |
σ + |
1 |
|
σ , |
||||||
|
Е |
Е |
||||||||||||
3 |
|
Е |
1 |
|
|
2 |
|
|
3 |
|||||
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
||
Еi ,νij =const; i, j =1, 2, 3.
Как определить константы, входящие в этот закон, показано в [1]. Их значения для талькохлорита и мрамора-II взяты здесь именно из [1], а для кварцевого диорита Д-2 [10]. Для этих пород константы упругости в предположении изотропности материала приведены в [11].
А.Н. Ставрогин [5] для определения пределов упругости предлагал использовать зависимость объемной деформации от среднего напряжения ( θ~ σ, где θ=ε1 +2ε2 , σ=(σ1 +2σ2 ) 3 ), причем за предельные
3 ), причем за предельные
упругие состояния принимаются точки, когда экспериментальные кривые этой зависимости отходят от линии гидростатического сжатия ( с =1). При этом на начальном участке диаграммы деформирования
118

О пределах упругости и прочности горных пород
осевая деформация ( ε1 ) должна быть пропорциональна осевому на-
пряжению. Анализируя полученные таким образом значения пределов упругости при различных видах напряженного состояния, приходим к выводу: точки, отвечающие значениям ( σ1e , ε1e ), действительно распо-
лагаются на соответствующем начальном участке диаграмм деформирования, но эти участки не отвечают закону Гука ни для изотропного, ни для ортотропного материала.
Иначе говоря, для каждого напряженного состояния значения предела упругости определялись эмпирически при использовании линейной аппроксимации начальных участков диаграмм σ1 ~ ε1 и зависи-
мости θ~ σ, что, в свою очередь, зависит в определенной мере от воли экспериментатора. Кроме того, остается непонятным, каким образом определять пределы упругости для тех напряженных состояний, для которых нет экспериментальных данных.
В данной работе предлагается следующий метод определения величин пределов упругости.
Предел упругости при одноосном сжатии определяем по методике А.Н. Ставрогина, т.е. для рассматриваемых материалов принимаем те их значения, которые даны в [5]. Но точку ( σ1e , ε1e ) на диаграмме
σ1 ~ ε1 откладываем не на экспериментальной кривой деформирования,
а на линии, отвечающей закону Гука для ортотропного материала. Затем таким же образом отмечаем пределы упругости (вычисляемые по указанным выше зависимостям) при произвольных напряженных состояниях.
Ниже, на рис. 3, приведены диаграммы деформирования, построенные по экспериментальным данным (сплошная линия) [5] для талькохлорита, мрамора-II и кварцевого диорита Д-2, линейные зависимости, построенные по закону Гука для ортотропного материала (штрихпунктирная линия) и для изотропного материала (штриховая линия), отмечены табличные (кругом) и расчетные (ромбом) значения пределов упругости.
119

Б.А. Рычков, Н.М. Комарцов, Т.А. Лужанская
а
б
Рис. 3. Диаграммы деформирования талькохлорита (а); мрамора-II (б); диорита Д-2 (в) при различных напряженных состояниях (см. также с. 120)
120
