книги / 635

21. Yamashita J., Asano S. Electronic structure of CsCl-type transition metal alloys // Progr. Theor. Phys. B. – 1972. – Vol. 48. – P. 2119–2131.

22. Алямовский С.И., Зайнулин Ю.Г., Швейкин Г.П. Оксикарбиды и оксинитриды металлов IVa и Va подгрупп. – М.: Наука, 1981. – 144 с.

Получено 3.09.2012

Жиляев Виктор Александрович – доктор технических наук, ведущий научный сотрудник лаборатории физико-химических методов анализа, Института химии твердого тела УрО РАН (620990, г. Екатеринбург, ул. Перво-

майская, 91, е-mail: zhilyaev@ihim.uran.ru).

Zhilyaev Victor Aleksandrovich – Doctor of Technical Sciences, Leading Research Associate, Institute of Solid State Chemistry, Ural Branch of RAS (620990, Yekaterinburg, Pervomayskaya st., 91, е-mail: zhilyaev@ihim.uran.ru).

21

УДК 621.1.9

Т.Р. Абляз, В.А. Иванов

T.R. Ablyaz, V.A. Ivanov

Пермский национальный исследовательский политехнический университет

Perm National Research Polytechnic University

РАСЧЕТ ВИБРАЦИИ ЭЛЕКТРОДА-ИНСТРУМЕНТА В ПРОЦЕССЕ ЭЛЕКТРОЭРОЗИОННОЙ ОБРАБОТКИ

CALCULATION OF WIRE ELECTROD VIBRATION

DURING ELECTRICAL DISCHARGE MACHINING

Представлено математическое описание вибрации электрода-инструмента в процессе электроэрозионной обработки.

Ключевые слова: электроэрозионная обработка, проволочно-вырезная электроэрозионная обработка, вибрация электрода-инструмента, электрод-инструмент, электрод-деталь.

In this work the mathematical description of the electrode-tool vibration in the EDM is presented.

Keywords: electrical discharge machining, wire electrical discharge machining, electrode vibration, electrod-tool, electrod-detail.

Задачей настоящего исследования является разработка математических моделей для расчета прогибов проволоки-электрода в процессе обработки детали на проволочно-вырезном электроэрозионном оборудовании.

Одним из существенных недостатков процесса электроэрозионной обработки (ЭЭО) является вибрация электрода-инструмента (ЭИ) в процессе резки. Данный недостаток сказывается на технологических параметрах электроэрозионного формообразования. Снижение влияния вибрации ЭИ на точность обработки является одной из основных задач в области развития ЭЭО.

Деформация ЭИ оказывает влияние на точность обработки в случае, когда он обладает малой жесткостью. Это в основном относится к операциям электроэрозионного вырезания (ЭЭВ). При ЭЭВ в качестве инструмента используется проволока диаметром 0,25–0,03 мм. Под воздействием силы, возникающей в межэлектродном зазоре при пробое, проволока прогибается на некоторую величину, в результате прогиба электрода-инструмента возникают погрешности обработки.

В нашей работе ЭИ рассматривается как металлическая струна, закрепленная на концах. Под струной в математической физике понимают гибкую упругую нить. Пусть струна натянута и закреплена на отрезке [0, l] оси ОХ.

22

Если усилием струну отклонить и придать ее точкам некоторую скорость, а затем отпустить, то точки струны будут совершать колебания.

При малых отклонениях струны от начального положения можно полагать, что точки струны движутся перпендикулярно оси ОХ и в одной плоскости, а функция, описывающая процесс колебаний, имеет вид u = u(x; t).

Рассмотрим элемент струны ММ1 (рисунок). На концах этого элемента по касательным к струне действуют силы Т. Пусть касательные образуют с осью ОХ углы φ и φ+∆ϕ. Тогда проекция на ось Ou сил, действующих на элемент ММ1, Тsin(ϕ+∆ϕ) −T sin(ϕ).

Рис. Профиль колебаний струны

Всилу малости φ и ∆x c точностью до O (∆x2 +∆ϕ2 ) можно записать

Тsin(ϕ+∆ϕ) −T sin(ϕ) =T tg(ϕ+∆ϕ) −T tg(ϕ) =

Для получения уравнения движения необходимо внешние силы, приложенные к элементу, приравнять к силе инерции. Если ρ – линейная плотность струны, то масса струны – ρ∆x. Cледовательно,

ρ∆x ∂2u =T ∂2u ∆x. ∂t2 ∂x2

Обозначая Tρ = a2 , получаем уравнение свободных колебаний струны

∂2u = a2 ∂2u . ∂t2 ∂x2

23

Если колебания вынужденные, то равнодействующая внешних сил, приложенных к участку струны ММ1 в момент времени t будет определяться как

F ≈ g(x,t)MM1 ≈ g(x,t)∆x.

Уравнение вынужденных колебаний струны

где форма записи g(x,t) зависит от участка, на котором действует данная си-

ла, и от закона распределения данной нагрузки.

Для приближения расчета к реальным условиям процесса ЭЭО необходимо рассмотреть колебания струны с учетом сопротивления окружающей среды. Силу сопротивления, возникающую при этом, примем пропорциональной скорости. Тогда на бесконечно малый участок струны M1M2 действует сила

Fсопр =α∂∂ut ∂x,

где α – коэффициент пропорциональности.

Сила сопротивления всегда направлена против движения, следовательно,

24

отсюда получаем

Поскольку краевые условия для функций X(х) остались такими же, как и для случая колебаний без сопротивления, то равенство (4) будет возможно,

если обе его части равны λ2k , где λk = nlπ – собственные числа (k = 1, 2, ...); при этом собственные функции Xk(x) определяются по формуле

Xk(x) = sin kπl x .

Для определения функций Tk(t) получим дифференциальное уравнение

Характеристическое уравнение имеет вид

Предположим, что коэффициент трения m настолько мал, что подкоренное выражение отрицательно для любых значений k. Данное условие будет

решение уравнения (1) будет иметь вид

25

Таким образом, решение уравнения (5) позволит определить деформацию ЭИ в процессе ЭЭО с учетом сопротивления окружающей среды.

Список литературы

1. Fundamental geometry analysis of wire electrical discharge machining in corner cutting / W.J. Hsue [et al.] // International Journal of Machine Tools & Manufacture. – 1999. – № 39. – Р. 651–667.

2.Абляз Т.Р. Изучение погрешности формы, возникающей при обработке криволинейных поверхностей на проволочно-вырезном электроэрозионном станке // Вестник ПГТУ. Машиностроение, материаловедение. – Пермь, 2011. – Т. 13, № 3. – С. 51–54.

3.Altpeter F., Perez R. Relevant topics in wire electrical discharge machining

control // Journal of Materials Processing Technology. – 2004. – № 149. – Р. 147–151.

Получено 3.09.2012

Абляз Тимур Ризович – аспирант, лауреат премии «Инженер года», Пермский национальный исследовательский политехнический университет

(614990, г. Пермь, Комсомольский пр., 29, е-mail: lowrider11-13-11@mail.ru).

Иванов Владимир Александрович – доктор технических наук, профес-

сор, Пермский национальный исследовательский политехнический универси-

тет (614990, г. Пермь, Комсомольский пр., 29, е-mail: msi@pstu.ac.ru).

Ablyaz Timur Rizovich – Postgraduate Student, Engineer of the Year award winner, Perm National Research Polytechnic University (614990, Perm, Komsomolsky av., 29, е-mail: lowrider11-13-11@mail.ru).

Ivanov Vladimir Aleksandrovich – Doctor of Technical Sciences, Professor, Perm National Research Polytechnic University (614990, Perm, Komsomolsky av., 29, е-mail: msi@pstu.ac.ru).

26

УДК 574.5

И.В. Анциферова, А.И. Зенков

I.V. Antsiferova, A.I. Zenkov

Пермский национальный исследовательский политехнический университет

Perm National Research Polytechnic University

ИДЕНТИФИКАЦИЯ ПОТЕНЦИАЛЬНО ОПАСНЫХ АСПЕКТОВ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА ПОЛУЧЕНИЯ ВЫСОКОПОРИСТОГО ПРОНИЦАЕМОГО ЯЧЕИСТОГО МАТЕРИАЛА НА ОСНОВЕ ХРОМАЛЯ

IDENTIFICATION OF POTENTIALLY DANGEROUS ASPECTS OF THE PROCESS OF OBTAINING HIGHLY POROUS PERMEABLE CELLULAR MATERIAL ON THE HROMAL BASIS

С использованием техники менеджмента качества и техники по оценке риска с учетом специфики производства проведена идентификация технологических аспектов, приводящих к возникновению дефектов, брака при производстве высокопористого проницаемого ячеистого материала на основе хромаля, а также проведена оценка воздействия ультрадисперсных порошков на окружающую среду и персонал, в результате которой можно принять объективные управленческие решения, направленные на постоянное улучшения процесса.

Ключевые слова: менеджмент качества, ультрадисперсные порошки, функциональное моделирование, шликерный способ, диаграмма Парето, ранжирование.

The article shows how to use quality management techniques and technology of risk assessment, taking into account the specifics of the production were identified by the technological aspects that lead to the appearance of defects in the production of highly porous marriage permeable porous material based on hromal, and an assessment of the impact of ultrafine powders of environmental environment and staff, as a result of which it is possible to make objective management decisions to continually improve the process.

Keywords: quality management, ultrafine powders, functional modeling, slip way, Pareto chart, ranking.

Система всеобщего менеджмента качества в настоящее время практически неразрывно связывается в цивилизованных странах с качеством и экологической безопасностью продукции. Экологический менеджмент и менеджмент качества понимаются как составная часть всеохватывающей системы, всеобщего менеджмента качества (рис. 1).

27

Всеобщий менеджмент качества

Менеджмент безопасности труда

Менеджмент безопасности производства

Менеджмент безопасности информации

Рис. 1. Области всеобщего менеджмента качества

Объем и содержание менеджмента качества, а также мероприятия по планированию, управлению, обеспечению и улучшению качества описаны в специальных руководствах по менеджменту качества. Внедрение менеджмента качества успешно осуществляется в рамках системы управления качеством окружающей среды. Важнейшими принципами этой системы являются:

–взаимосвязь всех действий по обеспечению качества;

–единодушное, целенаправленное планирование и проведение этих мероприятий и управление ими на предприятии.

Получить сертификат соответствия качества продукции экологическим стандартам можно лишь тогда, когда экологическим требованиям будет соответствовать вся технологическая цепочка ее изготовления, начиная с подготовки сырья и заканчивая последней технологической операцией. А для этого должна эффективно работать система экологического менеджмента [1].

В качестве основного фактора анализа выбираем внешние и внутренние требования к качеству процесса. Внешние требования устанавливаются, например, законами и нормативными документами, а также требованиями заказчика к сырью и материалам, эмиссии, производственной безопасности, возможности переработки отходов и экономичности.

Технологический процесс включает в себя прием в работу заготовок пенополиуретана, порошков, химических реактивов и материалов; подготовку щелочного раствора и щелочную обработку пенополиуретана; приготовление раствора поливинилового спирта; размол лигатуры Х52А20 до необходимого размера и приготовление смеси металлических порошков лигатуры, железа

икобальта; приготовление суспензии смеси порошков лигатуры, железа

28

и кобальта; нанесение шликерного покрытия на поверхность пенополиуретановой подложки; сушку и термообработку заготовки со шликерным покрытием; удаление структурообразующей пенополиуретановой подложки

иВМС-связки; окончательное спекание заготовки; деформацию спеченной заготовки; механическую обработку, калибровку ВПЯМ-пластин.

Для получения ВПЯМ-сплавов сложного состава пригодны шликерный

икомбинированный способы. Основные достоинства шликерного формования – возможность получения ВПЯМ с пористостью 85–96 % строго заданного состава с высокой гомогенностью и однородностью микроструктуры

имакроструктурой, подобной структуре пенополиуретана, т.е. с диаметрами открытых ячеек от 0,6 до 5 мм. Состав матрицы ВПЯМ полностью определяется составом использованного порошка или смеси порошков. Недостатком способа является то, что существуют ограничения на размеры получаемых изделий. Связаны они с величиной неизбежной усадки заготовок при спекании и с возрастающими при увеличении габаритов короблениями и деформациями.

Идентификация потенциальных несоответствий в процессе производства

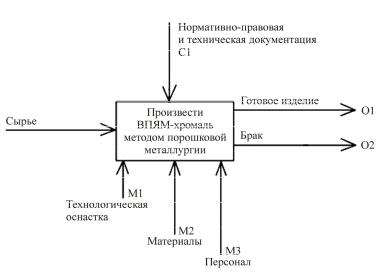
ивыделение проблемных вопросов в работе по контролю качества с помощью методологии функционального моделирования представлены в виде функциональной модели. В моделях (рис. 2, 3) описан процесс производства изделий методом порошковой металлургии.

Рис. 2. Модель А-0

Ввиду того, что основное количество брака наблюдается на стадии спекания, детально будет рассмотрен только узел операции спекания порошков

(рис. 4).

29