7

В частном случае, когда отрезок параллелен плоскости проекций, например отрезок МN, его проекция М1N1 конгруэнтна самому отрезку, так как они параллельны между собой. Прямые, параллельные плоскости проекций, называются прямыми уровня.

Из этого следует, что, если плоская фигура ограничена прямыми одного уровня, то она проецируется на параллельную плоскость проекций в конгруэнтную фигуру без искажения, в остальных случаях

–с искажением.

1.2.Теорема о частном случае проецирования прямого угла

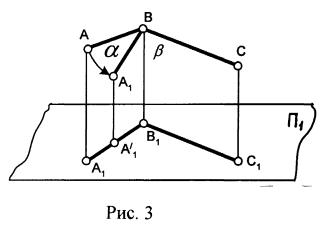
При прямоугольном проецировании прямой угол между отрезками прямых проецируется без искажений (прямым углом), если одна из его сторон параллельна плоскости проекций, а другая – не перпендикулярна к ней (рис. 3).

Доказательство: АВ^ С = 90°, допустим, что АВ и ВС || П1 Проеци-рующие плоскости α и β П1, (α β)∩П1 = А1 В^ 1 С1 = 90°.

Повернём в плоскости α прямую АВ в положение А1В, так, чтобы А1В стала прямой общего положения, сохранив при этом угол А1ВС = 90°. Эта теорема справедлива и для двух скрещивающихся прямых.

2. КОМПЛЕКСНЫЙ ЧЕРТЁЖ ТОЧКИ (ЭПЮР МОНЖА)

Две и более прямоугольные проекции геометрического образа, определяющие его форму, размеры и положение в пространстве, составляют комплексный чертёж, который называют метрически определённым, или обратимым.

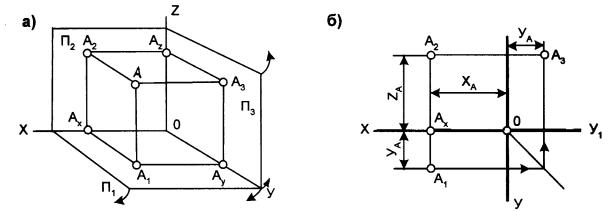
Положение точки в пространстве определяется её расстоянием (координатами) от выбранных трёх взаимно перпендикулярных плоскостей проекций. На рис. 4,а представлено аксонометрическое изображение плоскостей проекций: П1 – горизонтальная плоскость

8

проекций; П2 – фронтальная плоскость проекций; П3 – профильная плоскость проекций. Кроме этого, представлена точка А с

координатами (ХА, УА, ZА).

На рис.4,б показано построение комплексного чертежа точки А.

проекций: П1, П2, П3. Проекцию А1 называют горизонтальной проекцией точки А, проекцию А2 – фронтальной проекцией точки А, а проекцию А3 – профильной проекцией точки А (рис. 4,а).

Пользоваться для изображения предметов пространственной системой взаимно перпендикулярных плоскостей проекций сложно, поэтому её приводят к плоскому виду. Для этого горизонтальную плоскость проекций П1 вращением вниз вокруг оси Х совмещают с фронтальной плоскостью проекций П2. Профильную плоскость проекций П3 располагают справа от наблюдателя перпендикулярно одновременно горизонтальной П1 и фронтальной П2 плоскостям проекций (произошло совмещение плоскостей проекций с плоскостью чертежа). В результате получается трёхпроекционный комплексный чертёж точки А с осями х, у, z, где А1, А2, А3 соединяются прямой, называемой линией связи (см. рис. 4,б). Линия связи всегда перпендикулярна к оси проекций.

Основные свойства трёхпроекционного комплексного чертежа

(см. рис. 4,б):

две проекции точки принадлежат одной линии связи; линии связи перпендикулярны к соответствующей оси

проекций; две проекции точки определяют положение её третьей

проекции. Некоторые свойства прямоугольных проекций точки: точка в пространстве удалена от плоскостей проекций П1, П2 на величину удаления от оси соответственно её горизонтальной и

фронтальной проекций; положение точки в пространстве определяется её

ортогональными проекциями на две плоскости проекций (или тремя

9

координатами); если точка принадлежит плоскости, то одна из её проекций

совпадает с точкой, а две другие находятся на осях проекций.

Вопросы для самопроверки

1.В чём заключается сущность метода проекций ?

2.Какими плоскостями ограничены четверти пространства ?

3.По каким осям пересекаются плоскости проекций ?

4.Что называется комплексным чертежом точки ?

5.Что такое линия связи ?

3.ПРОЕКЦИИ ПРЯМОЙ

Прямая может быть задана аналитически (уравнением) и графически (проекциями). На чертежах прямую линию задают проекциями двух её точек.

Образование комплексного чертежа прямой аналогично образованию комплексного чертежа точки.

Прямые относительно плоскостей проекций занимают такие положения: общее, уровня, проецирующее.

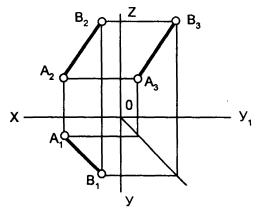
Прямые, не параллельные ни одной из плоскостей проекций, называются прямыми общего положения. Все проекции прямой общего положения не параллельны и не перпендикулярны линиям проекционной связи чертежа (рис. 5).

Рис. 5

3.1. Прямые уровня

Прямые, параллельные горизонтальной, фронтальной или профильной плоскостям проекций, называют соответственно горизонталь, фронталь, профильная прямая. Это – линии уровня.

Проекция отрезка прямой уровня на параллельную ему плоскость равна натуральной величине (НВ) отрезка, а углы, которые составляет эта проекция с линиями проекционной связи, равны углам

10

между самими отрезками и непараллельными им плоскостями проекций (рис. 6). Здесь α – угол наклона прямой к плоскости проекций П1, β – угол наклона прямой к плоскости проекций П2, γ – угол наклона прямой к плоскости проекций П3.

Рис. 6

3.2. Проецирующие прямые

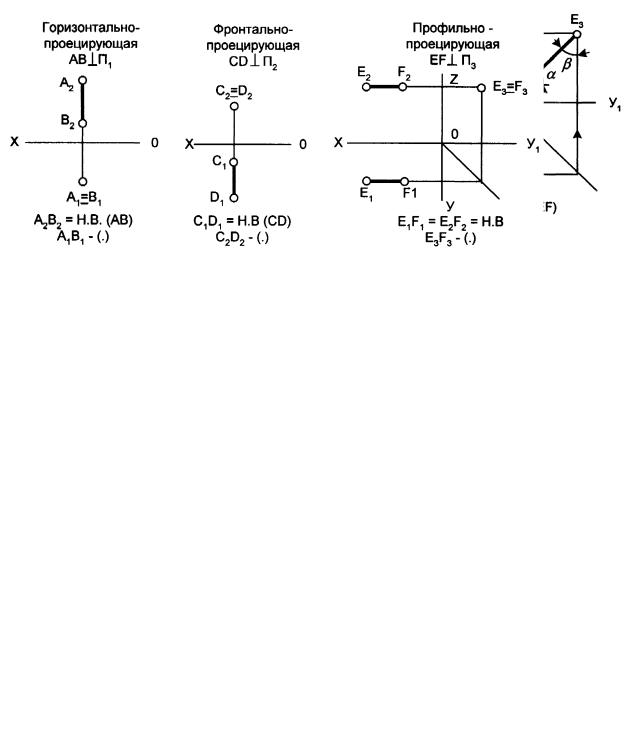
Проецирующие прямые – это прямые, перпендикулярные одной из плоскостей проекций. Эти прямые, будучи перпендикулярными одной плоскости проекций, оказываются параллельными двум другим плоскостям проекций. Поэтому у проецирующих прямых одна проекция превращается в точку, а две другие проекции совпадают на чертеже с направлением линии связи (рис. 7).

Рис. 7

Точки проецирующих прямых называют конкурирующими относительно соответствующих плоскостей проекций. Точки А и В,С и D, Е и F будут конкурирующими относительно П1; П2; П3.

11

Конкурирующие точки применяют при определении видимости на чертежах. Из двух горизонтально конкурирующих точек А и В на плоскости П1 видима та, которая выше, то есть А, а точка В оказывается под точкой А. Из двух фронтально конкурирующих точек С и D (рис. 7) на плоскости П2 видима та, которая ближе к наблюдателю, то есть точка D, а точка С невидима, так как расположена за точкой D.

Из двух профильно конкурирующих точек Е и F (рис. 7) на плоскости П3, видима та, которая левее, то есть точка Е.

3.3. Взаимное расположение двух прямых

Две прямые в пространстве могут пересекаться, скрещиваться и быть параллельными

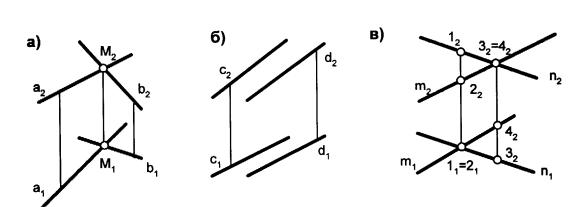
Пересекающиеся прямые – прямые, имеющие одну общую точку пересечения (а ∩ b = М, рис. 8,а). Следовательно, на основании свойства проецирования на комплексном чертеже точки М1 и М2 пересечения одноименных проекций прямых должны находиться на одной линии связи.

Рис. 8

Параллельные прямые – прямые, пересекающиеся в бесконечно удалённой точке (с || d, рис. 8,б). Следовательно, на основании свойства проецирования на комплексном чертеже одноименные проекции прямых должны быть параллельными.

Скрещивающиеся прямые – прямые, не имеющие общей точки (m и n, рис. 8,в). Следовательно, на основании свойства проецирования на чертеже точки пересечения одноименных проекций прямых не должны принадлежать одной линии связи.

3.4. Определение натуральной величины отрезка

Если отрезок прямой занимает общее положение, то определить истинную величину прямой на плоскостях проекций нельзя. Поэтому для определения длины отрезка по его проекциям используют способ

12

прямоугольного треугольника: длина отрезка измеряется гипотенузой прямоугольного треугольника, одним катетом которого является проекция отрезка на плоскость, а другим – разность расстояний концов его до этой плоскости. Рассмотрим прямую общего положения в пространстве.

Рис. 9

Треугольник АВВ1 – прямоугольный. Гипотенуза АВ является натуральной длиной отрезка (рис. 9,а), а проекция А1В1 – катетом. Второй катет ВВ1 определяет превышение одного конца отрезка над другим относительно плоскости проекций П1 и проецируется без искажения на фронтальную плоскость проекций П2. Угол α = ВАВ1 – это угол наклона прямой АВ к горизонтальной плоскости проекций.

Построения см. на рис. 9,б. Из точки В1 проведём перпендикуляр к проекции А1В1, отложим на нём отрезок В1Во = ВхВ2 и соединим прямой точки А1 и Во. Построенный треугольник А1ВоВ1 = АВВ1 (рис. 9,а), так как равны их катеты и угол между ними составляет 90°. Следовательно, отрезок А1Во равен отрезку АВ и угол В1А1Во определяет угол наклона отрезка АВ к горизонтальной

плоскости проекций.

Аналогичное построение можно сделать на фронтальной плоскости проекций, только в качестве второго катета нужно будет взять разность глубин его концов В1Вх (рис. 9,в).

Определение длины отрезка с использованием способа замены плоскостей проекций будем рассматривать в вузе.

Вопросы для самопроверки

1.Какое положение может занимать прямая относительно плоскостей проекций ?

2.Прямая общего положения (начертить комплексный чертёж).

3.В каком случае прямая обращается в точку и как называются