книги / 437

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Башкирский Государственный Аграрный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

σij = 2µεij + 2µv εij +

+δij λεkk +

εkk −3K (αp −αr )η−3ζ(αp −αr )η .

.pdf

Скачиваний:

Добавлен:

07.06.2023

Размер:

2.61 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 147 8 9 10 11 12 13 14 > Следующая >>>

В ходе нагрева и реакции в системе возникают внутренние напряжения (термические и химические), которые оказывают влияние на скорость химической реакции дополнительно к внешней нагрузке, а также при ее отсутствии. Свойства веществ в первом приближении считаются независящими от температуры и степени превращения.

2. Математическая постановка задачи

Математическая постановка задачи включает уравнение теплопроводности

cρρs

= λT T +Q dη

−

3KαTT dεkk

+ σV

dε

(1)

уравнение химической кинетики

dη

± k

= k0ϕ(η)exp

−

(2)

уравнение неразрывности

dρ

+ρ v = 0,

(3)

и уравнение движения

ρρs

= σ,

(4)

где Π = −∑σijεij ,

d...

= ∂...

+ v ...,

ϕ(η)

– кинетическая функция, с – тепло-

i, j

∂t

емкость при постоянных деформациях; ρs – плотность несжимаемой основы; ρ – относительная плотность, или величина, равная 1–π, где π – пористость; Т – температура, t – время, λT – коэффициент теплопроводности, Q – тепловой эффект химической реакции, η – степень превращения, K – изотермический модуль всестороннего сжатия, αT – коэффициент линейного теплового расширения, σij и εij – компоненты тензоров напряжений σ и деформаций ε, k0 – предэкспонент, Ea – энергия активации химической реакции, kσ – коэффициент чувствительности скорости химической реакции к работе напряжений, R – универсальная газовая постоянная, vr и vz – радиальная и осевая компоненты вектора скорости.

Уравнение теплопроводности (1) отличается от уравнения, используемого в классической теории термоупругости [9], наличием в правой части последнего слагаемого, учитывающего работу вязких напряжений [10].

Уравнение химической кинетики записано в виде (2) в соответствии с представлениями Эйринга–Козмана [11] о влиянии механических напряжений на скорость реакционного взаимодействия. Запись этого уравнения подразумевает, что действие напряжений облегчает либо затрудняет переход через энергетический барьер, но не влияет на его высоту.

Поскольку задача является осесимметричной, запишем все необходимые уравнения в цилиндрической системе координат. Будем полагать, что искомые величины зависят только от координат r, z и времени, тогда

εφφ = εrφ = εzφ = σφφ = σrφ = σzφ = 0. В двумерной постановке уравнение теплопроводности, связанное с деформациями, примет вид

∂2T

1 ∂T ∂2T

dη

dε

dεij

cρρs

= λT

∂r

2 +

r ∂r

∂z

−3KαTT

+σij

(5)

где

εkk = εrr +εzz .

Уравнения химической кинетики и неразрывности останутся прежними, а уравнения движения трансформируются следующим образом:

	∂σrr		1		∂σrz
ρρsvr =	∂r	+ r		σrr +		,
					∂z
	∂σrz		1		∂σzz	(6)

ρρsvz =		+		σrz +			.
	∂r		r		∂z

Начальные и граничные условия для уравнений (2), (3), (5) примут вид:

t = 0 : T =T0 , η = 0, ρ = ρ0 ,

r = 0:

∂T

T =Te ,

t ≤ th ,

∂r

r = R1

: λ

cos(γ) ∂T

+sin (γ)

∂T

= α

(T −T

t > t

∂r

∂z

T =Te , t ≤ th ,

∂T

z = 0 :

= σst (T

∂T

= αh (T −T0 ), t > th ,

z = L :

−λT

−T0

∂z

λT

∂z

Здесь R1 – это наружная граница камеры и пресс-формы, B = − R1 − R2 ,

C = R1 + L1 (R1 − R2 ), σst – постоянная Стефана-Больцмана, Te – температура

стенок и пресса; степень черноты тела принята равной единице, αh – коэффициент теплоотдачи.

3.Выбор реологических соотношений

Вработе использованы реологические соотношения трех типов.

Вгипоупругой модели приращения компонент тензора напряжений линейно связаны с приращениями компонент тензора деформаций, приращениями температуры и степени превращения:

e			,	(7)
dσij = 2µ dεij +δij λdεkk −3K (αT dT +(αB −αA )dη)

где λ, µ – коэффициенты Ламэ, K – коэффициент, учитывающий изменение объема вследствие несоответствия между конечной и начальной фазами,

K = λ + 23 µ, αВ – αА.

Соотношения (7) несложно переписать в виде

	dσije			λ	σkk		e	T	Y
dεij =		+δij	−			+αT dT +(αp −αr )dη	= dεij	+ dεij	+ dεij ,
dεij =	2µ	+δij	−	3K	2µ	+αT dT +(αp −αr )dη	= dεij	+ dεij	+ dεij ,
	2µ			3K	2µ

где первое слагаемое в правой части – это приращения обратимых деформации, вызванных упругими напряжениями, второе – приращения термических деформации; третье – приращения необратимых деформации, связанных с химической реакцией или фазовым переходом.

Модель вязкой среды (часто используемая для описания поведения порошковых сред в процессах прессования) [5, 6] основана на известной аналогии между инвариантами тензоров напряжений и деформаций [12]. Действительно, для упругой и вязкой сред имеют место соотношения:

	σije = 2µ εij +δijλεkk ,					(8)
V		ζ −	2		εkk ,	(9)
σij	= 2µV εij +δij	ζ −	3	µV	εkk ,	(9)
			3

где ζ – модуль объемной вязкости, µV – коэффициент динамической вязкости. Очевидно, что

σekk = 3Kεkk , σVkk = 3ζεkk .

(10)

Поскольку для термоупругого тела имеет место соотношение

σe	= 2µ ε	ij	+δ	λε	kk	−3Kα	T (	T −T		,
ij		ij		ij	kk		T (	0 )

то, пользуясь аналогией (10), запишем для вязкого тела соотношения

V		ζ −	2			(11)
σij	= 2µV εij +δij	ζ −	3	µV	εkk −3KαTT .	(11)
			3
						63

Вязкоупругая модель учитывает все названные эффекты. Разделим тензор напряжений на две составляющие: упругую и вязкую, σij = σije +σVij .

Поскольку состав среды в ходе химической реакции изменяется, то для упругих напряжений используем обобщенные соотношения Дюамеля– Неймана:

σije = 2µ εij +δij [λεkk − Kω ],				(12)
где
		n
ω = 3	αT (T −T0 ) + ∑		αk ηk ,
		k=1

n – число компонентов, участвующих в реакциях; ηk – их концентрации, αk – коэффициенты концентрационного расширения. По аналогии с предыдущим для вязких напряжений имеем

V		2			n
σij	= 2µV εij +δij ζ −	3	µV	εkk −3K αTT + ∑		αkηk .
		3			k=1

где ζ – это аналог K, ζ – 2µV/3 – аналог λ.

В результате придем к следующим соотношениям:

	ζ −	2
σij = 2µεij + 2µv εij +δij λεkk +	ζ −	3	µv	εkk − Kω−ζω
		3

или для суммарной реакции

Поведение материала в процессе экструзии с химической реакцией в настоящей работе исследовалось на основе всех выписанных моделей (7), (11) и (13). Заметим, что в работах [6, 13], посвященных анализу режимов синтеза в условиях экструзии, исследование напряженно-деформированного состояния не проводилось.

В цилиндрической системе координат в рассматриваемых условиях имеем дополнительные соотношения:

εzz =

dvz

, εrr =

dvr

, εrz =

dvr

dvz

(14)

Используя (13) и (14), вместо (6) запишем

dvr

∂2vr

∂2vz

ρρs

= ζ +

µv

∂r

∂r∂z

+µv

∂2vr

∂vr

ζ −

∂vz

∂z

2 +

ζ +

µv

∂r

∂z

+(λ+ 2µ)

∂εrr +λ ∂εzz

+ 2µ ∂εrz

− K ∂ω

−ζ

∂ω

∂r

∂z

∂r

+ 1

λ+ 2µ

)

+λε

− Kω−ζω .

(

dvz

∂2vz

µv

∂2vr

µv

∂vr

∂vz

ρρs

ζ +

µv

2 +µv

ζ +

∂r

∂z

∂r

∂r∂z

∂z

+2µ

∂εrz

+ 2µ

εrz

+(λ+ 2µ) ∂εzz

+λ ∂εrr

− K

∂ω −ζ ∂ω.

∂r

∂z

Условиями к «механической» части задачи будут: t = 0 : vr = vz = 0,

r = 0 : ∂vr =	∂vz = 0, r = R : v = v		z	= 0,
∂r	∂r	1 r

z = 0: vr = 0, vz =Vpr , z = L : vr = 0, vz =Vex (R12 −r2 ).

(15)

(16)

4. Замена переменных
Для численного исследования удобно сделать замену			переменных.
В области конуса, z [L1, L1 + L2 ] была сделана замена: x2	=		R1	r. В об-
В области конуса, z [L1, L1 + L2 ] была сделана замена: x2	=	Bz +C		r. В об-
		Bz +C

ласти выходного цилиндра – x3 = R1 r. Такое преобразование координат по-

зволяет работать с прямоугольной областью x [0, R1] для любых z. Это учтено и при записи определяющих соотношений. В пределах цилиндриче-

ской камеры x = r,			в области конуса x =	R1
					r, а в области выходного ци-
				Bz +C	r, а в области выходного ци-
линдра x =	R1	r.
линдра x =	R	r.
	R
	2

В безразмерных переменных

v = vr , v

= vz , r =

z =

, ω =

ω*

θ =

T −T

τ =

εij

σij

−T

где

λT

v* =

x* =

κT t* ,

κT

t* =

cρs RT*

exp

T* =T0 +

cρs

EQk0

RT*

cρs

ω* = ε* = 3αT (T* −T0 ), σ* = 3KαT (T* −T0 ),

задача принимает вид:

dθ

∂2θ

∂θ

∂2θ

−δ(θ+σ

)

+δsv

deij

dτ

∂x 2

∂x

∂z 2

dτ

dη

1−η

θ−1−δA(σT +1)∑ sijeij

exp

i, j

dτ

θ0

β(θ+σT )

∂ρ

ρv = 0.

∂τ

dvr

∂2vr

H1 ∂2vr

∂2vz

ρN

+ 1

−

dτ

∂r

∂z

∂r

∂z

∂vr

∂vz

1−

∂r

+(1− H1)

∂z

+ϕ

∂err

∂ezz

∂erz

−

3 −2h1

∂ω

−h

1−h

∂z

3 −3h

∂r

err +ezz −

3 −2h1 ω −ω*H1 ∂ω

1−h1

3 −3h1

∂r

ρN

dvz

2 ∂2vz

∂2vz

2 − H1 ∂2vr

∂vr

∂vz

∂z

∂r

∂r ∂z

∂z

∂r

∂e

1 ∂e

∂e

3 −2h

∂ω

+ϕ

−

−ω*H1

∂r

∂z

−3h1

∂z

−h1

∂z

ω= θ+ g η.

(17)

(18)

(19)

(20)

(21)

Граничные и начальные условия запишутся так:

τ = 0 : θ = 0,η = 0, vr = 0,vz = 0,

∂θ

θ = θe ,

τ ≤ τh

x = 0:

= 0,

x =

∂θ

∂x

R1 : R1 cos(γ)

+sin (γ)

= Nu

θ,

τ > τh ,

Bz +C

∂x

∂z

θ = θe ,

τ ≤ τh

∂θ

z = 0:

z =

: −

= P (θ+σ

−σ4

∂θ =

Nu θ, τ > τh ,

∂z

= 0 : ∂vr = 0,

∂vz = 0, x =

: v = 0, v

= 0,

∂x

: vr = 0, vz =Vex (

R12 − x 2 ),

z = 0 : vr = 0, vz =Vpr , z =

Vpr

2µ

λt ε

2µ

где

V =

L =

N =

, ϕ =

* ,

µv / ρs

µv

λ + 2µ

ζ +

µv

Nu =

αh x* , δ =

KαT ω* ,

σ =

, θ

, A =

kσQ

β =

RT*

λT

cρ

T* −T0

β(θ+σT )

g =

αp −αr

P =

σst x* (T* −T0 )3

αT (T* −T0 )

λT

Все безразмерные параметры имеют четкий физический смысл.

5. Алгоритм численного исследования задачи

Задача решалась численно. Поскольку уравнения (17), (20), (21) относятся к параболическому типу, для их решения использована схема переменных направлений, которая для уравнения

∂F	=	∂2F	+	∂2F	+ψ(x, z )
∂τ		∂x 2		∂z 2

принимает следующий вид [14]:

F n+1/ 2 − F n

F n+1/ 2

−2F n+1/ 2

+ F n+1/ 2

F n

−2F n

+ F n

i, j

= i+1, j

i, j

i−1, j

+ i, j+1

i, j

i, j−1 +ψn

∆τ/ 2

∆x 2

∆z 2

i, j

F n+1

− F n+1/ 2

F n+1/ 2

−2F n+1/ 2

+ F n+1/ 2

F n+1

−2F n+1 + F n+1

i, j

= i+1, j

i, j

i−1, j

+ i, j+1

i, j

i, j−1 +ψn

∆τ/ 2

∆x 2

∆z 2

i, j

где n – номер временного слоя, все первые производные вошли в функцию ψ. Для решения полученной системы конечно-разностных уравнений используется метод прогонки вдоль осей x и z.

Для решения уравнения (18) использована явно-неявная разностная схема. По переменной η схема неявная, а значения температуры и компонент тензоров напряжений и деформаций вычисляются предварительно в процессе решения уравнений (17), (20), (21) и считаются «замороженными».

ηn+1	−ηn		(1−ηin,+j1 )		θin, j −1−δA(σT +1)(sxxexx + syyeyy )n
i, j	i, j	=		exp			i, j	.
∆τ		=	θ0	exp	n	+σT )		.
∆τ			θ0		β(θi, j	+σT )

Время сгорания смеси tc отслеживалось по выполнению условия

	1	L R
		∫ ∫1 η(x, z)dxdz > 0,999.
	R L
		0 0
	1

Для проверки правильности работы программы проведено сравнение результатов расчетов с данными программного комплекса Elcut для следующего случая: камера (цилиндр и конус) заполнены порошковым реагентом,

насадок отсутствует, при z = L поставлено условие адиабатичности: ∂∂θz = 0,

осуществляется инертный прогрев смеси. В расчетах принято, что T0 = 0 °С, Te [500, 800] °С. Для проведения расчетов использовались данные для сме-

си 86 % Ni+14 % Al	[2, 15]: ρs = 6685 кг/м3, с =	660 Дж/(кг·К), λT =
= 123 Вт/(м·К), k0 = 105	с–1, E = 105 Дж/моль, Q = 8·109	Дж/м3, T = 1723 K,
		*

T0 = 300 K, R1 = 2 см, R2 = 1 см, L1 = 10 см, L2 = 10 см, µv = 6,5·10–3 Па·с,

ζ = 5,2·10–3 Па·с, αh = 400 Вт/м2/К, ρ0 = 0,5. При переходе к безразмерным параметрам это соответствует следующим значениям: β = 0,1, σT = 0,21, φ = 1,8,

H1 = 0,8, N = 31, P = 0,002…0,004, Nu = 6,5·10–4, R1 = 100, L1 = L2 = 500.

Для сравнения результаты расчетов температурного поля к моменту времени t = 9,5 c приведены в таблице.

Сравнение с результатами программного комплекса Elcut. Te = 600 °С

R, z	Температура (∆t = 150 мс), °С		Температура (∆t = 15 мс), °С
R, z	Elcut	Численный счет	Elcut	Численный счет
	Elcut	Численный счет	Elcut	Численный счет
R1/2, L1/2	585,29	585,76	586,48	585,77
R1/2, L1	586,60	587,18	587,97	587,17
R1/2, 3L1/4	583,97	584,58	585,24	584,59

Видно, что результаты отличаются не более чем на 0,1–0,2 %. Исследована сеточная сходимость. Выяснено, что при достижении ша-

гами по пространству значений ∆x = 2, ∆z = 4, шагом по времени – ∆τ = 1

идальнейшем их уменьшении значения расчетных величин отличаются менее чем на 1 %. Поэтому при численном исследовании использовались указанные значения шагов. Таким образом, расчетная область представляет собой прямоугольник 50·875 точек.

6.Пример расчетов

Впроцессе численного счета определялись и анализировались поля температуры, степени превращения, компонент скоростей и тензоров напряжений и деформаций.

Модель позволяет проводить исследования времени нагрева, при кото-

ром произойдет устойчивое воспламенение смеси τh, и его зависимости от параметров задачи. В результате расчетов получаем двумерные поля всех исследуемых величин, анализ которых позволяет делать выводы о динамике процесса. Для практических приложений представляет интерес оптимизация технологических параметров (таких как скорость плунжера, геометрическая форма и размеры камеры и матрицы, время начала экструзии и т.д.). В рамках модели возможно исследование влияния теплофизических параметров

иэффекта связанности на эволюцию напряженно-деформированного состояния смеси.

Большой интерес представляет сравнение реологических моделей. Наиболее отчетливо различие между ними проявляется на примере компо-

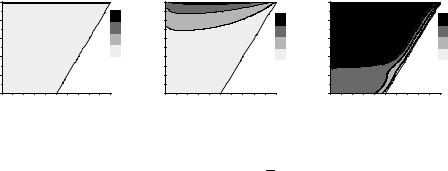
ненты скорости vz. На рис. 2 приведено распределение скорости в момент, когда пресс полностью прошел цилиндрическую камеру.

500	z						Vz	500	z
							Vz
600							0.10	600
							0.10
700							0.06	700
700							0.02	700
							0.02
800								800
900								900
1000	0	20	40	60	80	100	r	1000	0

					V	500 z							Vz
					z
					0,10	600							0,10
					0,10								0,10
					0,06	700							0,06
					0,02								0,02
						800
						900
20	40	60	80	100	r	1000	0	20	40	60	80	100	r

Рис. 2. Поле компоненты скорости: vz, а – вязкая модель, б – гипоупругая модель,

в – вязкоупругая модель; β = 0,1, δ = 0,03, A = 10, ρ0 = 0,5, vpr = 0,16, φ = 1,8, H1 = 0,8, N = 31, P = 0,003, Nu = 6,5·10–4, R1 = 100, τ = 3450

Как видно, вязкая модель (рис. 2, а) хуже всего описывает передачу возмущения от пресса к выдавливаемой среде. В случае гипоупругой модели (рис. 2, б), несмотря на отсутствие возмущений в большей части объема, занимаемого смесью, в выходной части насадка скорости достигает значительных величин. Это объясняется тем, что на каждом временном шаге на верхней подвижной границе задается профиль Пуазейля. По-видимому, требуются дополнительные соображения, чтобы задать корректное условие на верхней границе в гипоупругой модели. Наибольшее изменение осевой компоненты скорости наблюдается в рамках обобщенной вязкоупругой модели

среды (рис. 2, в).
500	z				ρ	500		z				ρ	500 z							ρ
					ρ							ρ								ρ
600					0,8	600						0,8	600							0,8
					0,8							0,8								0,8
700					0,7	700						0,7	700							0,7
700						700							700
					0,6							0,6								0,6
800						800							800
900						900							900
1000	0	30	60	90	r	1000	0	20	40	60	80	100 r	1000	0	20	40	60	80	100	r
			а							б							в

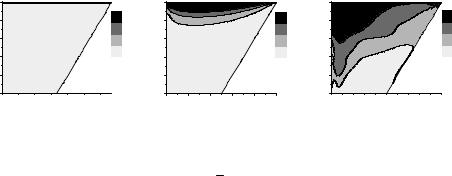
Рис. 3. Поле плотности: а – вязкая модель, б – гипоупругая модель, в – вязкоупругая модель; β = 0,1, δ = 0,03, A = 10, ρ0 = 0,5, vpr = 0,16, φ = 1,8, H1 = 0,8, N = 31, P = 0,003, Nu = 6,5·10–4, R1 = 100, τ = 3450

На рис. 3. представлены результаты расчетов поля плотности. Ситуация аналогична предыдущей: вязкая модель плохо отражает воздействие пресса на экструдируемый материал, в гипоупругой модели область с высокой плотностью насадка никак не соединяется с областью камеры, поскольку профиль Пуазейля задается только при z ≥1000. Вязкоупругая модель позволяет увидеть неоднородное распределение плотности по образцу, что чаще всего и имеет место на практике [16]. Дальнейшие расчеты предполагается проводить в рамках этой модели.

Библиографический список

1.Найбороденко Ю.С., Итин В.И., Савицкий К.В. Экзотермические эффекты при спекании смеси порошков никеля и алюминия // Известия ву-

зов. Сер. Физика. – 1968. – № 10. – С. 27–35.

2.Эволюция зеренной структуры интерметаллического соединения

Ni3Al при экструзии интерметаллида в процессе его высокотемпературного синтеза под давлением / В.Е. Овчаренко, О.В. Лапшин, В.А. Чудинов, Е.Г. Колобова // Физическая мезомеханика. – 2005. – Т. 8. – Спец. вып. –

С. 65–68.

<<< < Предыдущая 1 2 3 4 5 67 / 147 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в папке книги

#
07.06.20232.45 Mб1430.pdf
#
07.06.20232.48 Mб1431.pdf
#
07.06.20232.52 Mб1432.pdf
#
07.06.20232.57 Mб1434.pdf
#
07.06.20232.58 Mб1436.pdf
#
07.06.20232.61 Mб4437.pdf
#
07.06.20232.62 Mб1438.pdf
#
07.06.20232.62 Mб1439.pdf
#
07.06.2023249.05 Кб344-1.pdf
#
07.06.20234.36 Mб1544.pdf
#
07.06.20232.63 Mб13440.pdf