
книги / 437
.pdf
Механическое равновесие упругих материалов, содержащих жидкость
Рассмотрим неоднородно набухший образец эластомера или полимерного геля, который подвергнут внешнему механическому нагружению. Распределение растворителя в его объеме задано. Пусть Г1 – часть границы, на
которой действуют поверхностные силы g, а на другой ее части Г2 – заданы
перемещения. Обозначим Ω – область пространства, которое занимает образец в деформированном состоянии.
Состояние материала с произвольным распределением растворителя в общем случае не является термодинамически равновесным, что вызывает диффузию растворителя. Но диффузия и порождаемая им эволюция напря- женно-деформированного состояния образца – весьма медленные процессы, что позволяет считать текущее состояние сетчатого полимера механически равновесным [4–6].
Общая система уравнений, описывающая механическое равновесие упругого материала с заданным распределением жидкости в приближении несжимаемой смеси, имеет следующий вид [6, 7]:
|
T = 0, det F = J* (qk ), |
R Ω; |
(1) |
|
|
n T = g, (R Г1 ); R = R* (qk ), |
(R Г2 ); |
(2) |
|
|
T = FT (∂f/ ∂F)n ,n − pE, |
(3) |
||
|
1 |
2 |
|
|
где T |
– тензор упругих напряжений Коши, T = J −1FT P; F – тензор гради- |
|||
ента |
деформации; J = det F – третий инвариант градиента |
деформации; |
||
функция J* (qk ) характеризует распределение растворителя в объеме мате-
риала; qk , k =1,3 – система материальных координат, связанная с упругой матрицей; E – единичный тензор; n – внешняя нормаль в текущей конфигурации; p – действующее в смеси гидростатическое давление; f – плотность свободной энергии в деформированном состоянии; n1, n2 – кон-
центрация растворителя и упругой матрицы в текущем состоянии смеси соответственно.
Условие несжимаемости смеси задается соотношением |
|
J = ϕ02 / ϕ2 , |
(4) |
где ϕ2 , ϕ02 – объемная доля упругой матрицы соответственно в текущей и отсчетной конфигурации, J – характеризует локальное относительное из-
51

менение объема материала. Приближение несжимаемой смеси означает, что причиной изменения объемных деформаций материала является поглощение растворителя.
Упругие свойства сетчатых полимеров
Для описания упругих свойств высокоэластичных упругих материалов, содержащих жидкость, воспользуемся теорией полимерных сеток Флори– Ренера. Согласно этой модели плотность свободной энергии и тензор напряжений Коши имеют следующий вид [6]:
|
+χn1ϕ2 |
+ |
1 |
−2 3 |
ˆ |
|
|
ˆ |
= I1 |
|
ˆ |
/ J |
2 / 3 |
, |
ˆ |
2 / 3 |
, (5) |
f = R0T n1 ln ϕ1 |
2 |
n2ϕ2 |
I1 |
, |
I1 |
(B) = I1 |
|
B = B / J |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 1 3 |
ˆ |
− |
1 |
ˆ |
|
− pE, |
|
|
|
|
|
(6) |
|
|
T = R0TV2 ϕ2 |
B |
3 |
I1E |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где T – абсолютная температура; R0 – универсальная газовая постоянная; χ – параметр Флори – Хаггинса, I1 – первый инвариант меры деформации Фингера; V2 – мольный объем цепей полимерной сетки.
Напряженно-деформированное состояние неоднородно набухшего образца сетчатого полимера сферической формы
Рассмотрим неоднородно набухший образец полимерного геля или эластомера сферической формы. Определим его напряженно-деформирован- ное состояние.
Полагаем, что в исходном состоянии распределение растворителя в материале однородно. Это состояние используем в качестве отсчетного. В центр образца поместим сферическую систему координат (r, ϑ, ϕ) и свя-
жем ее с полимерной матрицей. Эти координаты выберем в качестве материальных.
Будем полагать, что растворитель – нелетучий и его общее количество в отсчетной и текущей конфигурациях остается постоянным. Распределение растворителя в объеме материала сферически симметрично и зависит только от радиальной координаты.
Пусть
e1 = er , e2 = eϑ, e3 = eϕ
52

– ортонормированный базис сферической системы координат в отсчетной конфигурации. Тогда радиус-вектор, определяющий отсчетную конфигурацию,
|
r = re1, e1 = e1(ϑ,ϕ). |
|
(7) |
|||
Ортонормированный и координатный базисы связаны соотношениями: |
||||||
r1 = ∂r ∂r = e1, r2 = ∂r ∂ϑ= re2 , |
r3 = ∂r ∂ϕ = e3r sin ϑ. |
(8) |
||||
Из (8) нетрудно найти фундаментальную матрицу в отсчетной конфи- |
||||||
гурации gij = ri rj , ее определитель |
|
|
|
|
|
|
|
g = (r2 sin ϑ)2 . |
|
(9). |
|||
С учетом (8) и (9) получаем взаимный базис: |
|
|
||||
r1 = e , |
r2 = r−1e |
2 |
, r3 = (r sin ϑ)−1e |
, |
|
|
1 |
|
|
3 |
|
|
|
векторы которого удовлетворяют условиям ri rj = δij . Отличные от нуля производные:
∂e1 ∂ϑ= e2 , ∂e2 |
∂ϑ= −e1, ∂e1 ∂ϕ = e3 sin ϑ, |
(10) |
∂e2 ∂ϕ = e2 cosϑ, |
∂e3 ∂ϕ = −(e1 sin ϑ+e2 cosϑ). |
(11) |
Положение частиц в деформированном состоянии (актуальную конфигурацию) представим следующим образом:
R = R(r), Θ = ϑ, Φ = ϕ,
R = R(r)e1.
Отсюда из известных соотношений тензорного анализа [8] находим координатный и взаимный ему базисы, соответствующие текущей конфигурации, а также градиент деформаций и меру деформаций Фингера:
R1 = λ1e1, |
R2 = λ2re2 , |
R3 = e3λ2rsinϑ, |
|
|
|
|||||
R1 = λ1−1e1, |
R2 = (λ2r )−1 e2 , |
R3 = e3 (λ2rsinϑ)−1 , |
(12) |
|||||||
λ = R′(r), |
λ |
2 |
= λ |
3 |
= R r , |
J = G g = λ λ2 |
, |
(13) |
||
1 |
|
|
|
|
1 |
2 |
|
|
||
|
|
|
G = λ λ2r2 sin ϑ, |
|
|
(14) |
||||
|
|
|
|
|
1 |
2 |
|
|
|
|
F = FT = λ1e1e1 +λ2 (e2e2 +e3e3 ),
53

2 |
2 |
(e2e2 |
+e3e3 ), |
ˆ |
ˆ 2 |
ˆ 2 |
(e2e2 |
+e3e3 ), |
B = λ1 e1e1 |
+λ2 |
B = λ1 e1e1 |
+λ2 |
|||||
λˆ k = λk 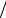 J1
J1 3 .
3 .
Здесь G – определитель фундаментальной матрицы, Gij = Ri R j в текущей
конфигурации; λk – главные относительные удлинения полимерной матрицы. Согласно (6) мера деформации Фингера и тензор упругих напряжений
соосны, поэтому
T = σ1e1e1 +σ2 (e2e2 +e3e3 ),
где σk – главные компоненты тензора напряжений Коши.
Учитывая (10) – (14), вычислим дивергенцию тензора T, используя из-
вестную формулу тензорного анализа [8] A = |
|
1 ∂ |
( GRk A), где A – |
|||||||||
|
|
|
|
|||||||||
|
G ∂q |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
k |
|
тензор второго ранга: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
∂σ1 |
|
2 |
|
|
|
|
|
|
|
T = e1 |
|
− |
|
(σ2 |
−σ1 ) . |
|
||||||
λ1 |
∂r |
rλ |
|
|
||||||||
|
|
|
2 |
|
|
|
|
|
|
|||
Таким образом, система уравнений (1)–(3), описывающая напряженнодеформированное состояние образца сетчатого полимера сферической формы, порождаемое неоднородным распределением растворителя, принимает следующий вид:
1 |
∂σ1 |
− |
2 |
|
(σ2 −σ1 ) = 0, J = λ1λ22 |
, |
(15) |
|
λ ∂r |
rλ |
2 |
||||||
|
|
|
|
|||||
1 |
|
|
|
|
|
|
||
|
|
|
σ1 = 0 при r = r0. |
|
(16) |
|||
Здесь r0 – радиус образца в отсчетой конфигурации, J = J (r) – заданная
функция, характеризующая распределение растворителя в объеме материала. Граничное условие вида (16) соответствует случаю, когда на всей границе образца задаются поверхностные силы. В данном случае поверхностные силы равны нулю, т.е. сетчатый полимер внешнему механическому нагружению не подвергается.
Из соотношений (13) получаем следующее дифференциальное уравнение:
R′(r) R2 = J (r), r2
решение которого
|
r |
|
R3 |
= 3∫ J (s)s2ds. |
(17) |
|
0 |
|
54
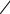
Постоянная интегрирования в (17) была найдена при условии R(0) = 0.
Соотношение (17) позволяет определить текущую конфигурацию частиц упругой матрицы по заданному распределению растворителя в образце.
Принимая во внимание условие несжимаемости (4), из соотношения (6) находим
σ |
|
= G J |
−1 |
λ |
2 |
− |
1 |
I |
|
− p, k = 1, 2, |
(18) |
k |
|
k |
|
|
|||||||
|
0 |
|
|
3 |
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
где G0 = RTV2−1 (ϕ02 )13 – модуль сдвига материала в отсчетном состоянии.
Из соотношения (18) следует, что
σ2 −σ1 = G0 J −1 (λ22 −λ12 ). |
(19) |
Подставив (19) в первое выражение (15) и проинтегрировав полученное выражение, имеем
r |
(1−λ12λ22 )ds. |
|
σ1 = −2G0 ∫0 (R(s))−1 |
(20) |
r
Константа интегрирования в (20) найдена с учетом граничного условия (16). Отсюда и из соотношения (18) получаем гидростатическое давление
p = G J −1 |
|
λ2 |
− |
1 I |
|
−σ . |
(21) |
|
0 |
|
k |
|
3 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
Полученные выражения (17)–(21) описывают напряженно-деформиро- ванное состояние неоднородно набухшего сферического образца при произвольном симметричном распределении растворителя. В качестве примера
рассмотрим случай квадратичного распределения растворителя J = J0 + kr2 ,
где параметр k характеризует степень неоднородности распределениям растворителя в образце.
Тогда аналитическое решение задачи (15)–(16) имеет вид
σ1 = −8 51/ 3 ω−1kr2 (5r0 + 4kr2 )(r −r0 ),
σ2 = −4 5−2 / 3 (Jω)−1kr2 (5r0 + 4kr2 )(kr2 (13r −10r0 ) +5J0 (3r −2r0 )), p =8 3 5−2/ 3 (Jω)−1kr2 (5r0 + 4kr2 )(3kr2 (6r −5r0 ) +5J0 (4r −3r0 )).
Здесь введено обозначение ω = (5J0 +3kr2 )2 (5J0r3 +3kr5 )1/ 3 .
55

На рис. 1–4 приведены результаты численного расчета напряженнодеформированного состояния образца при различных типах распределения растворителя. Кривые 1–3 соответствуют различным видам распределения растворителя, которые представлены на рис. 1, а, б. Зависимость действующего в шаре гидростатического давления от радиальной координаты показана на рис. 3.
|
|
|
|
|
|
а |
б |
Рис. 1. Различные типы распределения растворителя в образце: а – растворитель локализован на поверхности шара;
1− k =1,1(6), |
2 − k = 0,(6), 3 − k = 0,1(6); б – |
растворитель |
сосредоточен |
в центре шара; 1− k = −0,5, |
2 − k = −0,(3), |
|
3 − k = −0,1(6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
б |
Рис. 2. Распределение радиальных напряжений σ1 в сферическом образ-
це, порождаемое неоднородным распределением растворителя: а – соответствует распределению (1, а); б – соответствует распределению (1, б)
56

|
|
|
|
|
|
|
|
а |
б |
Рис. 3. Распределение напряжений σ2 в образце сетчатого полимера сфери-
ческой формы, порождаемое неоднородным распределением растворителя: а – соответствует распределению (1, а); б – соответствует распределению (1, б)
|
|
|
|
|
|
|
|
а |
б |
Рис. 4. Зависимость гидростатического давления в шаре от радиальной координаты: а – соответствует распределению (1, а); б – соответствует распределению (1, б)
Из рис. 4 видно, что в случае, когда растворитель локализован вблизи границы образца, то в его центре гидростатическое давление (в центре) отрицательно. Если же растворитель сосредоточен в центральной части образца, то в центре образца давление положительно. Это объясняется тем, что в первом случае более набухшие периферийные области материала стремятся расшириться, но их удерживает более «сухое» ядро в центре образца, которое оказывается подвергнутым (со стороны периферийных областей) воздействию растягивающих напряжений. Во втором случае, наоборот, более «сухой» периферийный слой оказывается в растянутом состоянии и стремится сократиться. Поэтому центр образца оказывается под воздействием сжимающих напряжений.
57
Заключение
Таким образом, в работе сформулирована нелинейная задача, описывающая напряженно-деформированное состояние неоднородно набухшего образца сетчатого полимера сферической формы с радиально симметричным распределением растворителя при конечных деформациях полимерной матрицы. В рамках теории полимерных сеток Флори–Ренера получено ее точное решение для различных типов распределения растворителя. Установлена зависимость внутренних напряжений, порождаемых неоднородным распределением растворителя, и гидростатического давления от радиальной координаты.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований и администрации Пермского края (коды проек-
тов: РФФИ 08-08-00541 и РФФИ – Урал 10-01-96031).
Библиографический список
1.Полимерные системы для контролируемого выделения биологически активных соединений / Л.И. Валуев, Т.А. Валуева, И.Л. Валуев, Н.А. Платэ // Успехи биологической химии. – 2003. – Т. 43. – С. 307–328.
2.Galaev I.Y., Mattiasson B. «Smart» polymers and what they could do in biotechnology // Trends in Biotechnology (TIBTECH). – 1999. – Vol. 17. – P. 335–340.
3.Моисеев Ю.В., Заиков Г.Е. Химическая стойкость полимеров в агрессивных средах. – М.: Химия, 1979. – 288 с.
4.Денисюк Е.Я., Терешатов В.В. Теория механодиффузионных процессов переноса многокомпонентных жидкостей в сшитых эластомерах // Прикладная механика и техническая физика. – 1997. – Т. 38, № 6. – С. 113–129.
5.Денисюк Е.Я., Терешатов В.В. Нелинейная теория процессов набухания эластомеров в низкомолекулярных жидкостях // Высокомолекулярные соединения А. – 2000. – Т. 42, № 1. – С. 71–83.
6.Денисюк Е.Я. Деформационное поведение полимерных сеток, содержащих растворитель или взаимодействующих с растворителем // Высокомолекулярные соединения А. – 2008. – Т. 50, № 6. – С. 1255–1268.
7.Денисюк Е.Я. Механика и термодинамика высокоэластичных материалов, насыщенных жидкостью // Механика твердого тела. – 2010. – № 1. –
С. 118–138.
8.Лурье А.И. Нелинейная теория упругости. – М.: Наука, 1980. – 512 с.
Получено 12.07.2010
58
УДК 531+536.46
Н.К. Евстигнеев
Томский государственный университет (г. Томск),
А.Г. Князева
Институт физики прочности и материаловедения СО РАН (г. Томск)
ВЫБОР РЕОЛОГИЧЕСКОЙ МОДЕЛИ ДЛЯ ОПИСАНИЯ СИНТЕЗА ИНТЕРМЕТАЛЛИДА, СОВМЕЩЕННОГО С ЭКСТРУЗИЕЙ ЧЕРЕЗ КОНИЧЕСКУЮ ПРЕСС-ФОРМУ
Mathematical model of self-propagating high-temperature synthesis of intermetallic compound combined with extrusion through a tapered die is suggested. Various rheological models of squeezingout media are used: viscoelastic, viscous, hypoelastic. Qualitative difference of the models is shown. All models take into account coupling effect between the fields of temperature, deformations and conversion degree. Model features are described.
Внастоящее время композиционные материалы на основе алюминидов никеля находят широкое применение в различных отраслях машиностроения. Прежде всего они используются в качестве защитных покрытий поверхностей деталей и узлов машин, подверженных разного рода деструктивным
воздействиям. В частности, интерметаллическое соединение Ni3Al применяется в качестве термостойкого и жаропрочного покрытия лопаток турбин авиационных двигателей. Получение этого соединения традиционными методами порошковой металлургии требует много времени и больших энергозатрат. Для решения этих задач применяют самораспространяющийся высокотемпературный синтез (СВС) в режиме теплового взрыва.
Входе реакции в некотором локальном объеме вещества выделяется тепло, которое прогревает соседние слои вещества и вызывает в них быструю химическую реакцию, таким образом обеспечивая перемещение реакционной зоны. Такое распространение зоны химической реакции используется для синтеза тугоплавких соединений, в том числе интерметаллидов, и получило название СВС в режиме горения. Повышение температуры во всем объеме системы вследствие тепловыделения в реакции приводит к картине, качественно подобной тепловому взрыву. Такой ход развития событий (СВС в режиме теплового взрыва) также пригоден для получения интерметаллидов [1].
59
Экспериментально установлено, что при использовании конической пресс-формы возможно получение субмикрокристаллической структуры в синтезированном интерметаллическом сплаве [2]. Проведенные эксперименты выявили необходимость оптимизации технологических процессов. Методы математического моделирования оказываются здесь весьма эффективными [3, 4], поскольку они позволяют не только более глубоко понять сущность процессов, но и существенно сократить число экспериментов.
Как правило, при описании реологии систем, подобных рассматриваемой, используются различные модели поведения среды – линейно вязкая [5, 6], нелинейно вязкая [7], пластическая [7]. Существуют также вероятност- но-статистические модели, описывающие макроструктуру порошка на этапе прессования [8]. Вопрос о применимости моделей в каждом конкретном случае остается открытым. В настоящей работе исследовано влияние реологических соотношений, соответствующих материалам с разными реологическими свойствами, на распределение температуры, степени превращения, компонент тензоров напряжений, деформаций и скоростей при варьировании геометрических размеров камеры, условий нагрева и нагружения.
1. Физическая постановка задачи
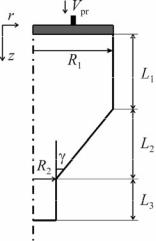
Считается, что процесс синтеза осуществляется в цилиндрической камере (I) с конической выходной частью (II), материал выдавливается в цилиндрический насадок (III). Радиусы отверстий и половина угла конической распушки матрицы γ заданы (рис. 1). В качестве реакционной смеси выбран порошок 3Ni+Al. За счет нагрева стенок камеры в течение заданного времени th. В камере в некоторый момент времени ti инициируется экзотермическая химическая реакция. При благоприятном стечении обстоятельств через время tc реакция полностью завершается.
В момент времени text > ti начинается выдавливание смеси веществ, содержащихся в камере, прессом со скоростью Vpr , много меньшей
Рис. 1. Иллюстрация к постановке задачи
скоростей распространения механических возмущений в системе. После прекращения химической реакции система остывает, что описывается в соответствии с законом теплообмена Ньютона. Химическую реакцию опишем суммарной реакционной схемой
A → B.
60
