книги / 393

метральной плоскости. Эта зависимость является следствием появления сдвиговых деформаций, которые отсутствуют в случае, когда и нагрузка, и само тело обладают одной и той же осью симметрии.

Обратим внимание на то, что в выражениях (16) для параметров ξi и ϕi под знак квадратного корня входят комплексы, состоящие из упру-

гих модулей материала. Поскольку вышеперечисленные параметры должны принимать только действительные значения, можно записать ограничения в форме неравенств на возможные величины упругих модулей материала иусловия существования решения при i >1:

В частном случае Er = Eθ = Ez = E , µrθ = µθz = µzr = µ и Grθ = G = E[2(1+ ν)], который соответствует изотропному тяжелому

горизонтальному цилиндру, новое аналитическое решение совпадает с результатом, полученным автором [2] с точностью до коэффициентов любого частного решения. Учет анизотропии материала позволяет установить связь между коэффициентами, входящими в равенства (12):

Покажем одно из возможных приложений найденного аналитического решения на примере задачи о равновесии тяжелого железобетонного цилиндра, наполовину закопанного в грунт. Предположим, что площадь контактной поверхности и реакция основания известны и неизменны во времени, а сама реакция распределена по боковой поверхности цилиндра по параболическому закону

41

нования в тригонометрический ряд по окружной координате. Эти условия позволяют определить постоянные интегрирования общих ре-

шений (10), (14) и (15).

Обратим внимание на то, что граничные условия (20) позволяют скомпенсировать дополнительные реакции только в радиальном направлении. Несмотря на то что при закреплении внутренней или внешней боковой поверхности возникают усилия в окружном и осевом направлениях, попытка компенсации этих реакций привела бы к получению решения с точностью до константы, отвечающей либо за вращение тяжелого цилиндра как жесткого целого вокруг оси симметрии, либо за перемещение в вертикальном направлении.

На рис. 2 представлено распределение перемещений точек поперечного сечения монолитного железобетонного цилиндра на внутренней, внешней и серединной поверхности по окружной θ и обезразме-

следующие параметры геометрии тела и упругие постоянные железо-

и µzθ = 0,375 .

Распределения перемещений по окружной координате носят немонотонный характер. Окружные перемещения являются нулевыми в точках, принадлежащих вертикальной диаметральной плоскости, в точках на внутренней, серединной и внешней поверхностях верхнего свода положительны, принимают свои максимальные значения при

θ = 90o , θ = 60o и θ = 45o. На нижнем своде в точках θ =125o , θ =115o

и θ =125o происходит смена знака, а θ =125o , θ =115o и θ =125o соответствуют точкам минимума для этих перемещений v на внутренней, серединной и внешней поверхности.

Радиальные перемещения на верхнем своде минимальны, возрастают по величине при увеличении окружной координаты. Эти перемещения на внутренней поверхности цилиндра всюду положительны,

43

на серединной поверхности принимают положительные значения

до θ =168o и имеют максимумы при θ =180o и θ =120o соответственно. На внешней поверхности зависимость u от окружной координаты

такова, что отрицательные значения имеют место при 0o ≤ θ ≤15o и 160o ≤ θ ≤180o, а максимальные значения достигаются при θ =115o .

Рис. 2. Распределение радиальных ( u,10−6 м) и окружных ( v,10−6 м)

перемещений в монолитном железобетонном цилиндре на внутренней, внешней и серединной поверхностях

Характер зависимостей перемещений точек, принадлежащих верхнему своду тяжелого цилиндра в направлении обезразмеренной радиальной координаты существенно изменяется при увеличении угла θ. Перемещения u монотонно убывают при θ = 0, монотонно возрастают при

θ = π2 и имеют точку локального минимума при θ = π4 . Зависимости ν~ ρ% имеют локальные максимумы, положение которых смещается ко внутренней поверхности цилиндра при увеличении окружной координаты.

Обратим внимание на еще одну закономерность распределения радиальных перемещений. Производные u по окружной координате

44

принимают нулевые значения

в точках поперечных сечений тяжелых ортотропных цилиндров, принадлежащих вертикальной диаметральной плоскости. Этот результат не зависит от того, на каком расстоянии от оси вращения находится рассматриваемая точка.

Библиографический список

1.Матвеенко В.П., Шевелев Н.А. Равновесие упругого и вязкоупругого горизонтального тяжелого цилиндра // Прикладные задачи теории упругости и вязкоупругости. – Свердловск: УНЦ АН СССР, 1976. – С. 77–83.

2.Кузнецов Г.Б. Упругость, вязкоупругость и длительная прочность цилиндрических и сферических тел. – М.: Наука, 1979. – 112 с.

3.Термопрочность деталей машин / И.А. Биргер, Б.Ф. Шорр, И.В. Демьянушко [и др.]. – М.: Машиностроение, 1975. – 455 с.

Получено 29.11.2010

45

УДК 593.3

А.В. Зайцев, А.А. Фукалов

Пермский государственный технический университет

ЭФФЕКТИВНЫЕ МОДУЛИ ОБЪЕМНОГО СЖАТИЯ ДИСПЕРСНО-УПРОЧНЕННЫХ КОМПОЗИТОВ СО СПЛОШНЫМИ И ПОЛЫМИ АНИЗОТРОПНЫМИ СФЕРИЧЕСКИМИ ВКЛЮЧЕНИЯМИ

В рамках полидисперсных моделей механики композитов получены аналитические выражения для эффективных модулей объемного сжатия дисперсно-упрочненных материалов, изотропные матрицы которых армированы трансверсально-изотропными полыми или сплошными сферами различного диаметра, а на межфазных поверхностях выполняются условия идеального сопряжения. На основе полученных решений спрогнозированы эффективные характеристики полиэфирной смолы «Диэпокс 450» для различных наполнений этого связующего мраморной мукой, а также полимербетонов со сплошными сферическими анизотропными мраморными, диабазовыми и гранитными минеральными включениями произвольного размера.

Ключевые слова: дисперсно-упрочненные композиты, анизотропные полные и сплошные сферические включения, полидисперсная модель, идеальный контакт на межфазной поверхности, эффективные модули объемного сжатия; полиэфирное связующее «Диэпокс 450», наполненное мраморной мукой; полимербетон.

Рассмотрим двухфазный композит, армированный сплошными или полыми сферическими включениями различного диаметра. Придерживаясь гипотез полидисперсных моделей механики [1], будем считать, что каждая сферическая частица произвольного радиуса RA окру-

жена слоем связующего толщиной RB − RA таким образом, что отношения c = RARB для каждого армирующего элемента и h = R0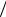RА для

каждого полого включения являются постоянными величинами. Кроме того, будем предполагать, что линейно упругая однородная матрица изотропна, а материал, из которого изготовлены включения, – сферически трансверсально-изотропный (ось симметрии бесконечного порядка совпадает с осью r сферической ортогональной системы координат r, θ и ϕ с началом в центре составной частицы.

Рассмотрим произвольное включение с неизменным типом упругой симметрии составных частей (частицы армирующего наполнителя и слоя матрицы), находящееся в состоянии однородного гидростатиче-

46

Рассмотрим наиболее простой случай, когда на межфазной поверхности выполняются условия идеального контакта

а внутренняя поверхность полых сферических включений свободна от напряжений:

Тогда из решения системы линейных алгебраических уравнений, которая получается при подстановке (4) и (5) в равенства (1) и условия (6), могут быть однозначно вычислены константы интегрирования:

BM = −(H1 − 6KM )HCRA3 ,

HC = p 4GM (H1 − 6KM )c3 + 3KM (H1 +8GM ) −1 ,

если композит армирован сплошными сферическими включениями. В случае, когда включения являются полыми, подстановка (3) и (4) в выражения (1) и условия (6) и (7) позволяет записать систему алгебраических уравнений и решить ее относительно неизвестных постоянных интегрирования:

AI = 2H2HI (4GM + 3KM )RA32−n , BI = 2H1HI (4GM + 3KM )h2nRA32+n ,

H7 =16A12H5 (A12H4 −6GM KM H6),

H8 = 8A11{A12H4H5 +3H6KMGM 2n(h2n +1)− H5 }.

Если предположить, что армирующие элементы однородно распределены внутри композита, то рассматриваемая среда квазиоднородна и сферически трансверсально-изотропна. Поставим в соответст-

48

включений, а также получить оценки снизу для эффективных модулей K*θϕ из равенства радиальных напряжений на внешних границах эквивалентных однородных включений

Несложно показать, что эти оценки совпадут с полученными выражениями (8) и (9). Следовательно, полученные решения являются точными в рамках ограничений, используемых в полидисперсных моделях. Обратим также внимание на то, что при подстановке R0 = 0 в уравне-

ния (9), последние упрощаются и принимают вид (8).

В частном случае E%I = EI = 9GI KI (3KI + GI ) и υ%I = υI = (3KI − 2GI )(6KI + 2GI ) из выражений (8) и (9) следуют эффективные модули объемного сжатия двухфазных дисперсноупрочненных композитов, изотропная матрица которых содержит однородно распределенные изотропные ( n =1,5) сплошные

и полые

K* = 4GI KI (1− h3)(4vIGM + 3K(M )+ G)M KM (1− vI )(4GI + 3h3KI )(11) 3KI h3 + 4GI (1− vI ) 1− h3 + 4GI (4GM + 3vI KM )

сферические включения. Обратим внимание на то, что в формулах (10) и (11) проведена замена c3 = vI (где vI — объемное наполнение),

а равенство (10) в точности совпадает с выражением, впервые записанным З. Хашином [1].

В качестве примера рассмотрим задачу прогнозирования эффективных модулей объемного сжатия полимербетонов – дисперсноупрочненных композитов на основе полиэфирных смол, армированных

50