книги / 41

нормальному распределению. При построении доверительного интервала для медианы сначала нужно упорядочить по величине полученные значения количественного параметра. Если упорядоченные значения обозначить х1, х2 ,..., хn, то доверительные границы

медианы, независимо от характера распределения исследуемого морфометрического параметра задаются формулой:

Для n > 50 значение h можно вычислить по формуле

Доверительные интервалы для относительных частотных показателей при np или n(1− p) > 5 удобно определять с помощью ап-

проксимации биномиального распределения нормальным распределением. Из выражения (4) легко получить формулу для определения минимального объема выборки, необходимого для обеспечения заданного уровня относительной погрешности :

Так как при увеличении числа степеней свободы t-распределение стремится к нормальному, критические значения z для любого уровня значимости можно найти в последней строке (при v = ∞) таблицы с критическими значениями t - критерия. Легко заметить, что np достигает максимума при максимуме р(1− р),то есть при

р = 0,5. Поэтому в случаях, когда перед началом исследования отсутствуют данные о частоте обнаружения исследуемого признака, можно рассчитать необходимый объем выборки, принимая р = 0,5.

Например, при разработке способа идентификации гестационного возраста нами рассматривалась возможность использования в указанных целях данные об изменении доли портальных трактов, содержащих желчные протоки. Требуемая относительная погрешность равнялась 1%. Тогда необходимое количество подлежащих изучению портальных трактов каждой печени с надежностью, рав-

ной 95%, составило np = 1,962 0,5 0,5/ 0,012 = 9604.

Для устранения погрешностей, связанных с количественной оценкой свойств исследуемой генеральной совокупности гистоструктур органа или ткани, целесообразно использование во всех случаях унифицированной тактической схемы, которая включает в себя следующие этапы:

41

-установление перечня морфометрических параметров, подлежащих количественной оценке;

-проведение поискового исследования для определения вида и свойств распределения изучаемого морфометрического параметра;

-определение необходимой степени точности исследования;

-определение минимального объема выборки, обеспечивающего получение количественной оценки исследуемого показателя генеральной совокупности микрообъектов (единиц наблюдения 2 уровня) данного органа или ткани (единицы наблюдения 1 уровня) с выбранной степенью точности;

-морфометрическое изучение определенного количества случайно выбранных микрообъектов в небольшой группе единиц наблюдения 1 уровня и фиксация результатов морфометрии;

-анализ полученных результатов и определение необходимого количества единиц наблюдения 1 уровня, исходя из задач исследования и вида последующих методов статистического анализа.

Для повышения воспроизводимости результатов количественных гистологических исследований следует учитывать также погрешности, обусловленные влиянием усадки тканей, неоднородности толщины срезов и аналитических тест-систем [54].

Таким образом, приведенные математические способы позволяют определять минимальное количество микрообъектов, необходимое для получения достоверной количественной оценки интересующего морфометрического параметра исследуемого органа с любой требуемой погрешностью. Возможности методов охватывают не только морфометрические показатели, подчиняющиеся нормальному закону, но и параметры, характеризующиеся другими видами непрерывных распределений, а также различными дискретными распределениями. Однако использование любых, даже самых сложных, математических приемов не освобождает от необходимости обеспечения рандомизации исследования и контроля погрешностей измерительной аппаратуры.

42

ГЛАВА 2. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ

2.1. ЗАДАЧИ КОРРЕЛЯЦИОННОГО АНАЛИЗА ПРИ СУДЕБНОМЕДИЦИНСКОЙ ИДЕНТИФИКАЦИИ ЛИЧНОСТИ

Одним из приоритетов судебно-медицинской антропологии является разработка и совершенствование способов прогнозирования каких-либо параметров идентифицируемых объектов, выраженных количественными признаками. К числу основных идентифицируемых параметров, обладающих таким свойством, относятся биологический возраст, длина тела, различные соматические размеры человека. Этим судебно-медицинское прогнозирование отличается от судебно-медицинской классификации, под которой понимается отнесение объекта экспертного познания к одному из нескольких взаимоисключающих классов, которые не могут быть описаны количественно (пол, соматотип, массивность скелета, порядковая локализация однотипных костей и др.).

Задачей научных исследований, посвященных созданию способов судебно-медицинского прогнозирования, являются поиск и изучение взаимосвязей между идентифицируемыми параметрами и идентифицирующими признаками и последующее построение математической модели, с определенной точностью позволяющей прогнозировать значение идентифицируемого параметра по значению идентифицирующего признака или группы признаков.

Искомые взаимосвязи между идентифицируемыми и идентифицирующими признаками, проявляющиеся в изменении статистических характеристик распределения одного признака с изменением другого, называются статистическими (стохастическими, случайными). Противоположность стохастической связи представлена функциональной зависимостью, когда факториальный признак полностью определяет прогнозируемый параметр (такие связи называются также детерминированными или жесткими).

В отличие от функциональной зависимости, дисперсия значений идентифицируемого параметра в статистических взаимосвязях не полностью определяется влиянием идентифицирующего признака (признаков). Более того, статистические взаимосвязи, как правило, не отражают истинный характер причинно-следственных связей.

Математической моделью, лежащей в основе создаваемых способов судебно-медицинского прогнозирования идентифицируемых

43

параметров, является корреляционно-регрессионный анализ, который включает в себя измерение тесноты, определение направления

иустановление аналитического выражения связи [79]. Корреляция

ирегрессия тесно связаны между собой: первая оценивает выраженность статистической связи, а вторая отражает ее форму.

Внастоящее время корреляционный анализ (корреляционная модель) определяется как метод статистического анализа взаимозависимости нескольких признаков, применяемый тогда, когда данные наблюдений или эксперимента можно считать случайными и выбранными из генеральной совокупности, распределенной по многомерному нормальному закону [26].

Основным фактором, определяющим видовую структуру методов корреляционного анализа, следует назвать количество идентифицирующих признаков идентифицируемых объектов. В качестве идентифицирующих обычно выступают разнообразные биометрические показатели человека, характеризующиеся каким-либо непрерывным распределением, чаще всего подчиняющимся нормальному закону.

Внаиболее простом варианте прогнозирование идентифицируемого параметра может производиться всего лишь по одному биометрическому признаку. Одним из основных показателей взаимозависимости двух случайных величин является парный коэффициент корреляции, служащий мерой линейной статистической зависимости между этими величинами. Этот показатель соответствует своему прямому назначению, когда статистическая связь между соответствующими признаками генеральной совокупности линейна. Как правило, более точное прогнозирование достигается по нескольким, наиболее информативным признакам, отобранным из множества характеристик, описывающих идентифицируемые объекты. Основным условием адекватности многомерного корреляционного анализа также является требование линейности статистических связей. Указанные требования выполняются, если генеральная совокупность распределена по многомерному нормальному закону.

Таким образом, диагностическая значимость результатов исследований, посвященных разработке способов судебно-медицинского прогнозирования идентифицируемых параметров, зависит от степени соответствия исходных данных тем условиям, наличие которых предполагает использованный метод корреляционного анализа.

44

2.2. ДВУМЕРНАЯ МОДЕЛЬ КОРРЕЛЯЦИОННОГО АНАЛИЗА

Двумерная модель корреляционного анализа лежит в основе статистической взаимосвязи пары признаков, один из которых является идентифицируемым, а второй - идентифицирующим. Как правило, двумерный корреляционный анализ используется на этапе поиска и отбора наиболее информативных признаков для последующего их включения в состав многофакторной регрессионной модели. Вместе с тем двумерный корреляционный анализ при идентификации личности по-прежнему имеет и самостоятельное значение.

Это нашло подтверждение проведенным нами специальным исследованием3. Целью его явилось изучение эпидемиологии и адекватности применения корреляционного анализа в научных работах, посвященных судебно-медицинской антропологической идентификации. Объектами анализа выступили 12 случайно отобранных статей, отображающих результаты оригинальных исследований, посвященных разработке способов прогнозирования идентифицируемых параметров, из числа работ, опубликованных в журналах «Су- дебно-медицинская экспертиза» и «Проблемы экспертизы в медицине» за период 2001-2006 гг. Протокол исследования включал также выявление всех опубликованных в журнале «Судебномедицинская экспертиза» в течение 2001-2005 гг. оригинальных исследований, выводы которых базировались на результатах применения каких-либо методов аналитической статистики и последующий отбор исследований, в которых использовался корреляционный анализ.

Проведенное исследование показало, что определение силы связей с помощью парных коэффициентов корреляции, имевшее место в 29,8% (25) оригинальных исследований, явилось вторым по частоте применения методом статистической обработки данных, незначительно уступив лишь сравнительному анализу с использованием критерия Стьюдента (31,0%). Применительно к судебномедицинским исследованиям, посвященным созданию способов идентификации личности на основе корреляционно-регрессионного анализа, двумерная модель последнего в качестве самостоятельного метода статистического анализа данных, использовалась в 5 (42%) статьях (95% доверительный интервал: 15-72%).

3 На результаты этого исследования опираются все эпидемиологические данные, приводимые в главе 2.

45

Математической моделью однофакторного корреляционного анализа является генеральная совокупность двух признаков, совместное распределение которых задано плотностью двумерного нормального закона.

С помощью выражения (1) можно доказать, что плотность двумерного нормального распределения задается функцией:

Изложенное означает, что плотность двумерного нормального распределения определяется пятью параметрами: математическими ожиданиями µ1 и µ2 случайных величин х1 и х2, их стандартными отклонениями σ1 и σ2 и коэффициентом парной корреляции ρ, который в двумерной модели является единственным параметром тесноты связи.

Коэффициент корреляции ρ представляет собой меру линейной зависимости двух переменных. Для коэффициента корреляции ρ двумерной генеральной совокупности справедливо:

1)−1 ≤ ρ ≤ +1;

2)при ρ = ±1 имеется функциональная зависимость, совокуп-

ность значений пар признаков представляет собой прямую; 3) из равенства ρ = 0 следует стохастическая независимость

признаков двумерной нормально распределенной генеральной совокупности;

4) чем ближе значение ρ к единице, тем сильнее коррелированы две случайные переменные;

5)при ρ < 0 имеет место отрицательная корреляция, когда с увеличением одной переменной вторая в среднем уменьшается;

6)при ρ > 0 имеет место положительная корреляция, когда с увеличением одной переменной вторая в среднем увеличивается.

Двумерное нормальное распределение может быть графически представлено колоколообразной пространственной поверхностью. Сечение указанной поверхности горизонтальной плоскостью при

ρ= 0 и σ1 = σ 2 , образует окружность, а при σ1 ≠ σ 2 - эллипс, су-

жающийся при ρ → 1 (рис. 2).

46

Рис. 2. Графики двумерного стандартного нормального распределения при ρ = 0 (верхний рисунок) и ρ = 1 (нижний рисунок).

47

Точечной оценкой параметра ρ тесноты связи между переменными х1 и х2 является выборочный парный коэффициент корреляции Пирсона r, который вычисляется как среднее произведение нормированных отклонений:

Статистическая значимость выборочного коэффициента корреляции, т.е. гипотеза о том, может ли выборочный коэффициент корреляции иметь случайные отклонения от нуля при генеральной совокупности с параметром ρ = 0, проверяется по Р.А. Фишеру на основании t-распределения с v = n − 2 степенями свободы

Существенность выборочного коэффициента корреляции также может быть проверена на основании F-распределения с помощью статистики

F = r2 (n − 2) при v1 = 1 и v2 = n − 2 [130].

Для значимых параметров связи имеет смысл найти интервальные оценки. Для этого служит статистика, введенная Р.А. Фишером:

1 r +1

zr = 2 ln1− , (6) r

которая при n > 10 распределена приблизительно нормально со

Тогда доверительный интервал для ρ с надежностью 1-α задается выражением

Для перехода от zr к ρ используется специальная таблица [30]. Указанная таблица позволяет получить интервальные оценки ρ ви-

ρ

да rmin ≤ ρ ≤ rmax , пренебрегая поправочным членом 2(n −1) у ρ.

48

Использование двумерной и других моделей корреляционного анализа можно показать на примере исследования гестационной динамики различных гистоструктур печени и селезенки человека на протяжении 21-40 недель антенатального развития, проведенного нами с целью создания способов судебно-медицинской идентификации гестационного возраста плодов и новорожденных [11,53].

Объектами данного исследования явились трупы 140 плодов и новорожденных. Морфометрическому исследованию были подвергнуты следующие показатели печени: кроветворная активность паренхимы, толщина соединительнотканной капсулы, относительные объемы стромы и долек. В селезенке оценивались толщина капсулы на диафрагмальной поверхности, диаметр и плотность расположения лимфоидных узелков, толщина стенок центральных артерий, относительные объемы белой пульпы, трабекулярного компонента и красной пульпы.

Входе количественного исследования использовалась стандартная методика изготовления гистологических срезов с поддержанием величин коэффициентов усадки на неизменном уровне. Толщина капсулы печени и все относительные объемные показатели оценивались в 31 наблюдении, гистометрические показатели селезенки исследовались в 99, а степень кроветворной активности печени - в 140 наблюдениях. На всех этапах морфолого-статистического анализа использовались истинные количественные характеристики абсолютных морфометрических показателей.

Вцелях отбора морфометрических показателей, пригодных для использования в качестве факторных признаков для идентификации гестационного возраста, на первоначальном этапе исследования проводился корреляционный анализ для определения характера

истепени тесноты связей между гестационным возрастом и исследовавшимися морфометрическими параметрами.

Одним из результатов исследования явилось основанное на изучении 99 наблюдений обнаружение умеренной положительной за-

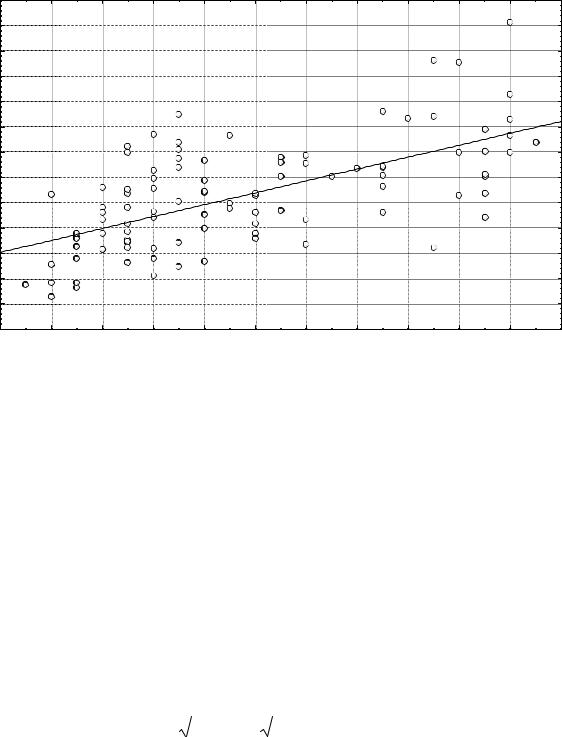
висимости (r = 0,633; r 2 = 0,400) диаметра лимфоидных узелков от гестационного возраста (рис. 3).

Проверим значимость оцененного коэффициента корреляции с помощью t-распределения с v = n − 2 степенями свободы:

49

Рис. 3. Зависимость диаметра лимфоидных узелков фетальной селезенки от гестационного возраста. По оси абсцисс – гестационный возраст, недель; по оси ординат – диаметр лимфоидных узелков, мкм.

Аналогичный результат получаем с использованием F-критерия:

Для определения интервальных оценок рассчитаем статистику

Тогда 95% доверительный интервал для ρ задается пределами 0,546 < zr < 0,946.

Отсюда получаем интервальные оценки ρ и ρ 2 : 0,496 < ρ < 0,736; 0,246 < ρ 2 < 0,542,

указывающие, что доля общей дисперсии показателя диаметра лимфоидных узелков селезенки, объясняемая гестационной динамикой, с 95% вероятностью находится в пределах 24,6—52,2%.

50