книги / 41

сии, доверительную область для прогнозных оценок регрессионных уравнений приближенно можно вычислить как

) ± .

уi уi zα sε

Погрешность в определении интервальных оценок у в данном случае может быть вызвана только неточностью выборочной оценки sε , которую можно ликвидировать, используя вместо sε ее одностороннюю верхнюю доверительную границу для любого требуемого уровня значимости, вычисляемую с помощью χ 2 - критерия.

Неадекватности интервальных оценок у при неоднородности

дисперсии остатков можно избежать, если при их вычислении в каждой точке регрессионной линии использовать не общую для всех значений независимой переменной величину sε , а рассчитан-

ную для каждого возможного значения х величину скользящего остаточного стандартного отклонения sε Х и его односторонней

верхней доверительной границы. При таком подходе доверительные границы для прогнозных оценок регрессионных уравнений являлись бы «плавающими», расширяясь на отрезках регрессионной линии с большим sε и сужаясь на отрезках, где sε невелико.

В соответствии с алгоритмом метода остатки упорядочиваются по возрастанию соответствующих значений независимой переменной с формированием ряда ε1;ε 2 ;K;ε n-1;ε n . Затем, последователь-

но «скользя» вдоль ряда, определяется sε X по k значениям остатков

со сдвигом на одно значение. При этом для каждого значения независимой переменной вычисляется скользящее остаточное стандартное отклонение с формированием ряда

ряется в начале и в конце упорядоченного ряда хi ). Далее для каж-

151

после чего формируются n − k +1 пар наблюдений х и соответствующих им значений sε ХВi .

В целях определения для любого возможного значения хi величины sε ХВi необходимо найти функцию зависимости sε ХВ от х. Для

этого нужно добиться наиболее адекватного сглаживания значений sε ХВ любым из существующих методов. В случае успешной ап-

проксимации доверительную область для прогнозных оценок рег-

тую наиболее адекватным методом подгонки полученных значений sε ХВi является LOWESS – сглаживание, обеспечивающее располо-

жение всех наблюдений sε ХВi на аппроксимирующей кривой

[95,96]. Недостатком LOWESS – сглаживания является необходимость графической визуализации зависимости sε ХВ от х вследствие

невозможности ее представления в формульном виде. Немаловажным моментом для выполнения указанной процедуры является выбор величины k , который определяется правилом: чем меньше k , тем лучше sε ХВi соответствует истинному значению sε в данной

точке линии регрессии; чем больше k , тем меньше величина sε ХВi и,

соответственно, уже доверительный интервал для прогнозных оценок регрессионной модели. По мнению авторов метода при анализе выборок объемом более 100 наблюдений наиболее адекватным является значение k , соответствующее 21.

Изложенный метод расчета доверительных границ может быть использован и при наличии в составе регрессионной модели нескольких факторных переменных. В данном случае упорядочивание остатков производится по возрастанию прогнозных оценок зависимой переменной, после чего определяются ряды значений скользящего остаточного стандартного отклонения sεY) и его одно-

сторонней верхней доверительной границы sεY)B . После успешной аппроксимации значений sεY)B доверительная область для прогноз-

ных оценок многофакторной регрессионной модели определяется по формуле:

152

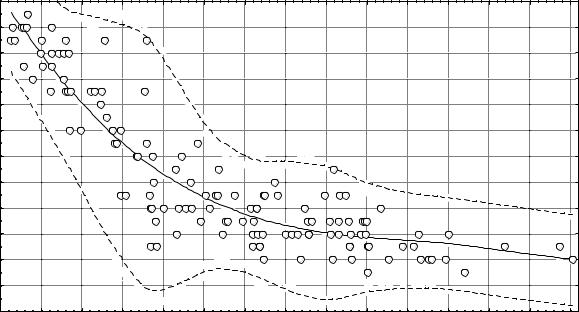
Метод скользящего остаточного стандартного отклонения был многократно использован нами при определении доверительных интервалов для прогнозных оценок разнообразных регрессионных моделей идентификации гестационного возраста плодов и новорожденных. Результатом явилось создание комплекса номограмм, позволяющих определять 50,60,70,80,90,95 и 99% интервальные оценки гестационного возраста [11,53]. Фрагмент одной из таких номограмм приведен на рисунке 28.

Таким образом, изложенный метод скользящего остаточного стандартного отклонения позволяет при наличии гетероскедастичности определять доверительные интервалы для прогнозных оценок любых (в том числе нелинейных и многофакторных) регрессионных уравнений. Данный метод более эффективен по сравнению с рекомендуемым при неоднородности дисперсии остатков методом взвешенных наименьших квадратов.

Рис. 28. Номограмма определения точечных и 95% интервальных оценок гестационного возраста плодов и новорожденных по степени кроветворной активности паренхимы печени. По оси абсцисс – кроветворная активность с учетом усадки, число профилей ядер миелоидных клеток; по оси ординат – гестационный возраст, недель. Сплошной линией показано множество точечных оценок, пунктирными линиями – множества 95% интервальных оценок гестационного возраста. На диаграмме маркирована выборочная совокупность наблюдений.

153

3.9. АВТОКОРРЕЛЯЦИЯ

Кроме гомоскедастичности второй предпосылкой адекватности метода наименьших квадратов относительно природы исследуемых данных и результатов регрессионной модели является отсутствие автокорреляции. Автокорреляцию (серийную корреляцию) можно определить как корреляционную зависимость между рядом y1, y2 ,K, yn и этим же рядом, сдвинутым относительно первона-

чального положения на h моментов времени y1+h , y2+h ,K, yh+n . С

автокорреляцией обычно сталкиваются, когда данные, по которым строится регрессия, являются значениями временных рядов. Такой тип данных представлен в таблице 18.

Различают два вида автокорреляции:

1)автокорреляция в наблюдениях за переменными;

2)автокорреляция ошибок.

Автокорреляцию в наблюдениях за одной или более переменными измеряют при помощи нециклического коэффициента автокорреляции, который может рассчитываться между уровнями, сдвинутыми на любое число единиц времени. Это сдвиг, именуемый временным лагом, определяет и порядок коэффициентов автокорреляции: первого порядка (при L = 1), второго порядка (при L = 2) и т.д. Считается, что наиболее сильные искажения результатов анализа возникают при корреляции между исходными уровнями и теми же уровнями, сдвинутыми на одну единицу времени [72]. В этом случае коэффициент автокорреляции можно определить как корреляцию между рядами y1, y2 ,K, yn−1 и y2 , y3 ,K, yn . Достоверность ко-

эффициента автокорреляции проверяют с помощью тех же методов, что и для обычного коэффициента парной корреляции.

Таблица 18 Данные временных рядов для множественной регрессии [78]

154

Однако несоответствие условиям применимости методов классического регрессионного анализа возникает при другом виде автокорреляции - серийной корреляции остатков. В этом случае нарушается одно из основных допущений о свойствах остатков εi регрессионной модели – свойство их статистической независимости между собой. При наличии серийной корреляции остатков искажаются стандартные ошибки коэффициентов регрессии, и все критерии существенности для уравнений регрессии не применимы даже для приблизительных расчетов.

Поскольку теоретические значения ошибок εi являются неизвестными, на практике исследуются их аналоги – остатки еi. Коэффициент автокорреляции первого порядка, имеющий наибольшее практическое значение, рассчитывается по формуле:

Для обнаружения автокорреляции остатков используется критерий Дарбина-Уотсона (DW):

i=1

Втеории доказано, что статистику Дарбина-Уотсона можно вы-

разить через коэффициент автокорреляции: DW ≈ 2(1− re ) .

При полной независимости остатков re = 0, а DW = 2. При положительной серийной корреляции re → +1, а 0 ← DW . При отрицательной серийной корреляции re → −1, а DW возрастает до 4.

Дарбин и Уотсон доказали, что существуют две границы, обозначаемые dU и dL, которые зависят лишь от объема выборки n, числа k независимых переменных и уровня значимости α [106,107]. Значения этих границ табулированы, поэтому результаты теста ДарбинаУотсона можно представить в виде следующей таблицы (табл. 19).

Обычно считается, что автокорреляция имеет место практически только при изучении временных рядов и характерна преимущественно для анализа экономических процессов [72,74,78]. Примени-

155

тельно к судебно-медицинским антропологическим исследованиям автокорреляцию можно ожидать в случаях, когда изучаемые биометрические показатели регистрируются на объектах различной давности, когда стохастическое изменение исследуемых показателей обусловлено процессами акселерации, произошедшими со времени формирования объектов научного поиска. Указанное замечание может быть существенным, поскольку материалом многих современных способов идентификации служили разнородные костные коллекции: например, коллекция кафедры антропологии МГУ давностью 50 лет, дополненная скелетами из захоронений XVII – XVIII веков [42], биометрические данные R. Povilaitis, дополненные серией скелетов кафедры антропологии МГУ [38].

Изложенное делает целесообразными включение в исследование объектов схожей давности, контроль времени формирования объектов и итоговое тестирование наличия серийной корреляции остатков. Например, сбор исходных данных для разработки способов идентификации гестационного возраста был произведен на коротком отрезке времени длиной менее двух лет. Результатом явилось отсутствие серийной корреляции остатков. Так, для регрессионной модели идентификации гестационного возраста по кроветворной активности печени re = 0,090; DW = 1,703; р > 0,05. Резю-

мируя, следует отметить, что наличие автокорреляции в судебноантропологических исследованиях можно вообще не контролировать, если объекты исследования характеризуются схожей давностью. Примером таких данных является сводка соматометрических характеристик шведов, умерших в 1971 г. [156].

156

3.10. СРАВНИТЕЛЬНЫЙ АНАЛИЗ РЕГРЕССИЙ

Необходимость сравнения двух или более линий регрессии в су- дебно-медицинских антропологических исследованиях встречается редко. Вместе с тем указанный аспект регрессионного анализа может быть источником важной информации о характере изучаемых зависимостей. Основным показанием к использованию сравнительного анализа регрессий в судебно-медицинской антропологии чаще всего является задача обнаружения кластеринга в исследуемых данных. Иногда указанная группа статистических методов может быть использована для решения обратной задачи – доказательства отсутствия выраженного кластеринга в исследуемой совокупности данных и возможности проведения регрессионного анализа для объединенной выборки. Например, при разработке регрессионных моделей идентификации гестационного возраста плодов и новорожденных помимо уже упомянутых причин кластеринга нами исследовалась также возможность влияния на степень кроветворной активности фетальной печени таких патологических процессов, как хроническая плацентарная недостаточность и внутриутробное инфицирование [55]. Проведенное исследование подтвердило большую выраженность экстрамедуллярного гемопоэза у плодов с названной патологией. Однако отсутствие выраженных различий между линиями регрессии в группах плодов и новорожденных от физиологически протекающей беременности и беременности с указанной патологией сделало возможным проведение регрессионного анализа для объединенной совокупности наблюдений [55].

Методы сравнения регрессий различаются в зависимости от количества сравниваемых линий, формы регрессионных зависимостей и количества переменных, входящих в состав регрессионных уравнений.

Рассмотрим наиболее простой случай – сравнение двух однофакторных линейных регрессий. Данную задачу можно выполнить тремя методами: сравнением коэффициентов сдвига b0, сравнением коэффициентов наклона b1 и сравнением линий регрессии в целом [16].

Сравнение коэффициентов двух однофакторных линейных регрессий производится однотипно по формуле:

tα ;v=n1+n2 −4 = bs1b1−−bb22 ,

157

где стандартная ошибка разности вычисляется как

sb1−b2 = sb21 + sb22 ,

если обе регрессии оценены по одинаковому числу наблюдений. В противном случае необходимо предварительно определить объединенную оценку остаточной дисперсии:

sε2 = (n1 − 2)sε21 + (n24− 2)sε22 . n1 + n2 −

Тогда стандартная ошибка разности для коэффициента наклона

Аналогичная формула для стандартной ошибки коэффициента

Изложенные методы пригодны лишь для сравнений двух однофакторных линейных регрессий. Если вместо статистик х и sx ис-

пользовать соответствующие линеаризирующие преобразования, то методы сравнений регрессионных коэффициентов могут быть легко преобразованы для сравнений однофакторных нелинейных регрессий.

Сравнение линий регрессии в целом позволяет осуществлять сравнительный анализ многофакторных и нелинейных регрессий с различным количеством независимых переменных в их составе. Пусть сравнению подлежат m регрессий, каждая из которых содержит ki независимых переменных. Тогда алгоритм метода включает выполнение следующих этапов.

1.Производится подгонка регрессии для каждой k-мерной выборки из общего их числа m.

2.По остаточным дисперсиям sε2i каждой из регрессий вычисляется объединенная оценка остаточной дисперсии

i=1

158

3. Осуществляются объединение выборок, подгонка регрессии, включающей К независимых переменных, для единой выборки и

вычисление ее остаточной дисперсии sΣ2 .

4. Вычисляется эффект использования раздельных регрессий, мерой которого служит величина:

5. Вычисляется статистика

F = s2ε . sε2

6. Полученная статистика сравнивается с критическим значением F-критерия при требуемом уровне значимости α и числе степе-

m

ней свободы v1 = m и v2 = ∑(ni − ki −1). Если полученное значение

i=1

F-критерия больше критического, то гипотеза о совпадении линий регрессии должна быть отклонена.

Для примера продолжим сравнительный анализ возрастной динамики объема головного мозга у мужчин и у женщин (см. раздел 2.7). Напомним, что в рамках данного исследования было произведено измерение объема головного мозга от трупов 61 мужчины и 32 женщин, умерших в возрасте 18-92 лет. Сравнительный анализ корреляций значимых межполовых различий в скорости развития церебральной атрофии не обнаружил. Попытаемся выявить указанные различия методами сравнения регрессий.

Визуальное изучение диаграмм рассеяния и сравнение остаточных дисперсий альтернативных регрессионных моделей возрастной динамики объема головного мозга показало, что исследуемые зависимости по форме являются линейными и могут быть представлены следующими аналитическими выражениями:

где VM – объем ГМ у мужчин, мл; VW – объем ГМ у женщин, мл; х – возраст, лет; t – значение двустороннего варианта критерия Стью-

159

дента при требуемом уровне значимости α и указанном количестве степеней свободы.

Сравним коэффициенты наклона указанных регрессий. Результаты промежуточных вычислений и некоторые параметры регрессий приведены в таблице 20.

Таблица 20 Параметры регрессий и выборочных совокупностей

Вычислим объединенную оценку остаточной дисперсии:

sε2 = (n1 − 2)sε21 + (n2 − 2)sε22 = 15442,611. n1 + n2 − 4

Отсюда стандартные ошибки разности равны

Таким образом, сравнительный анализ не выявил различий между угловыми коэффициентами регрессий. Вместе с тем, при одностороннем варианте t-критерия обнаружены различия по коэффициентам сдвига регрессий ( р = 0,046). Полученные данные свиде-

тельствуют об отсутствии межполовых различий в скорости церебральной инволюции, что подтверждается результатами сравнительного анализа коэффициентов корреляции (см. раздел 2.7), и наличии межполовых различий между средними значениями объема головного мозга. Геометрическая интерпретация полученных выводов приведена на рисунке 29.

160