
ИДЗ3
.pdf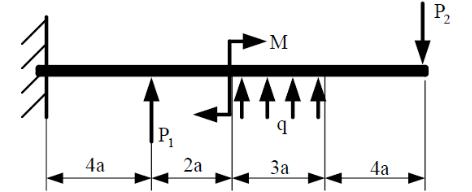
/ = / + / + / + / + / = 0.015 − 0.017 − 0.008 − −0.002 − 0.003 = −0.015
ЗАДАЧА 3. ИЗГИБ
Металлическая балка находится под действием сосредоточенных внешних сил, распределенной нагрузки, сосредоточенного изгибающего момента. Величины нагрузок приведены в табл. 5. Длину а, во всех вариантах принять равной 2м. Физико-механические характеристики материала стержня: Е=2·105
МПа; [Δl]=3·10-4 мм; [σ]=160 МПа.
Для заданной схемы балки, требуется:
1.Составить аналитические выражения и определить реакции в опоре.
2.Построить эпюры поперечных сил и изгибающих моментов.
3.Подобрать размеры поперечного сечения: двутавровое; круглое –
диаметром d.
В масштабе изобразить поперечные сечения балки.
Исходные данные:
Расстояние а=2 м;
Изгибающий момент М=14 кНм;
Сосредоточенная сила P1=40 кН;
Сосредоточенная сила P2=60 кН;
Распределенная нагрузка q=15 кН/м;
Рис. 7 Схема
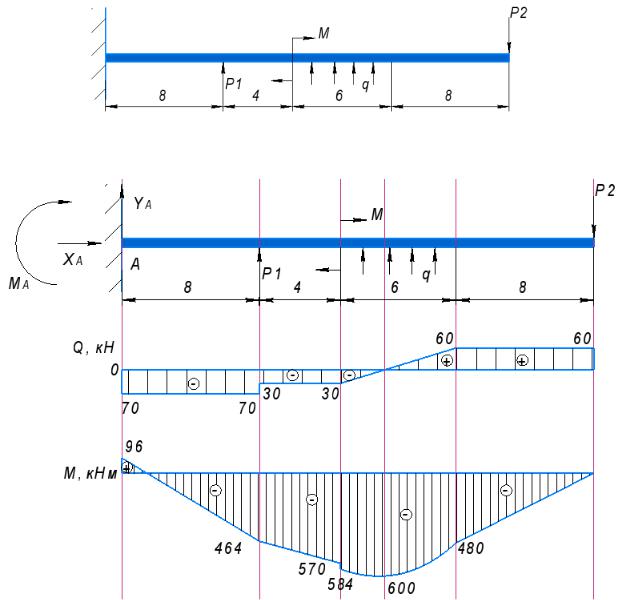
Рис. 8 Схема в KOMPAS
Рис. 9 Эпюры сил и моментов Определим реакции в опоре А:
Xa=0
∑ = + 1 − 2 + ∙ 6 = 0= − 1 + 2 − ∙ 6 = −40 + 60 − 6 ∙ 15 = −70 кН
∑= − + 8 ∙ 1 − 26 ∙ 2 + 15 ∙ ∙ 6 − = 0= 8 ∙ 1 − 26 ∙ 2 + 15 ∙ ∙ 6 − = 96 кНм Сечение 1:
∑= 0 ; ∑ М = 0
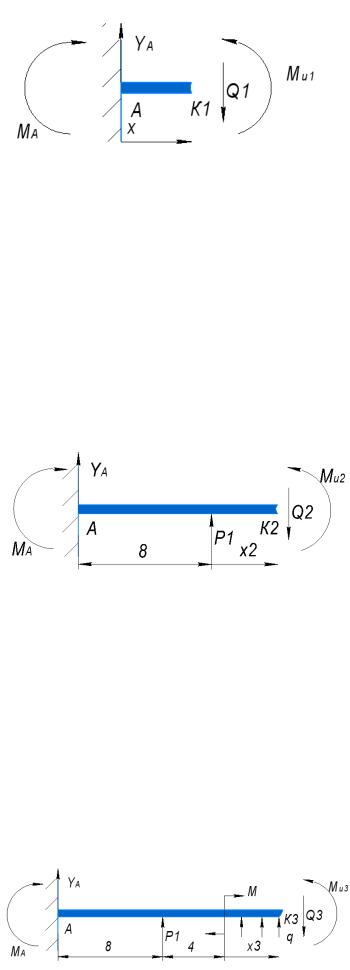
∑= − 1 = 0= 1 = −70 кН
∑М = − + и1 − ∙ = 0 ; 0 ≤ 1 ≤ 8 ;и1(0) = = 96 кНми1(8) = + ∙ 8 = 96 − 70 ∙ 8 = −464 кНм Сечение 2:
∑= 0 ; ∑ М = 0
∑= − 2 + 1 = 0
2 = + 1 = −70 + 40 = −30 кН
∑М = − + и2 − 2 ∙ 1 − ∙ (8 + 2) = 0 ; 0 ≤ 2 ≤ 4 ;и2(0) = + 8 ∙ = 96 − 70 ∙ 8 = −464 кНм
и2(4) = + 4 ∙ 1 + ∙ (8 + 4) = 96 + 40 ∙ 4 − 70 ∙ 12 = −584 кНм Сечение 3:
∑= 0 ; ∑ М = 0
∑ = − 3 + 1 + ∙ 3 = 03 = + 1 + ∙ 3 = −70 + 40 + 15 ∙ 3; 0 ≤ 3 ≤ 6 ;
3(0) = + 1 = −70 + 40 = −30 кН3(6) = + 1 + ∙ 6 = −70 + 40 + 15 ∙ 6 = 60 кН
∑ М = − + и3 − − (4 + 3) ∙ 1 − ∙ 3 ∙ 23 − ∙ (12 + 3) = 0 ;
и3(0) = + + 4 ∙ 1 + ∙ 12 = 96 + 14 + 160 − 840 = −570 кНми3(6) = + + (4 + 6) ∙ 1 + ∙ 6 ∙ 62 + ∙ (12 + 6) = −480 кНм
Графиком изгибающего момента является парабола. Рассчитаем вершину параболы:
|
|
(− − ) |
|
(70−40) |
|||||||
В = − |
|
= |
|
1 |
= |
|
|
|
= 2 |
||
|
|
|
|
15 |
|||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
2 2 |
|
|
||||
|
|
|
|
|
|
|
|
||||
и3(2) = + + (4 + 2) ∙ 1 + ∙ 2 ∙ 22 + ∙ (12 + 2) = 96 + 14 + 6 ∙ 40 + 15 ∙ 2 − 70 ∙ 14 = −600
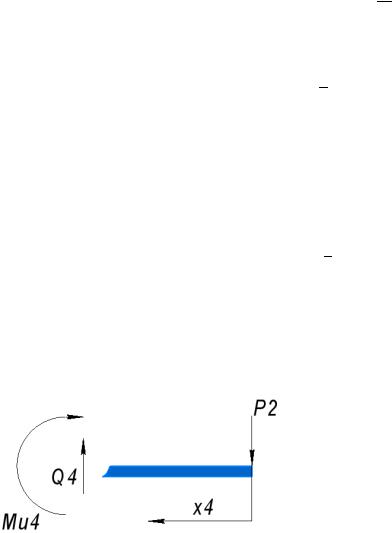
Сечение 4:
∑ = 0 ; ∑ М = 0
∑= 4 − 2 = 04 = 2 = 60 кН
∑М = и4 + 4 ∙ 2 = 0 ;и4(0) = 0 кНм
и4(8) = −8 ∙ 2 = −480 кНм
Подобрать размеры поперечного сечения балки из условия прочности
≥ (Ми).расч = 600∙103 ≥ 0.00375(м3)
[ ] 160∙106
Для круглого сечения балки диаметр d равен:
|
|
|
|
|
= |
∙ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
32∙ |
3 |
32∙0.00375 |
|
|
|
= √ |
|
= √ |
|
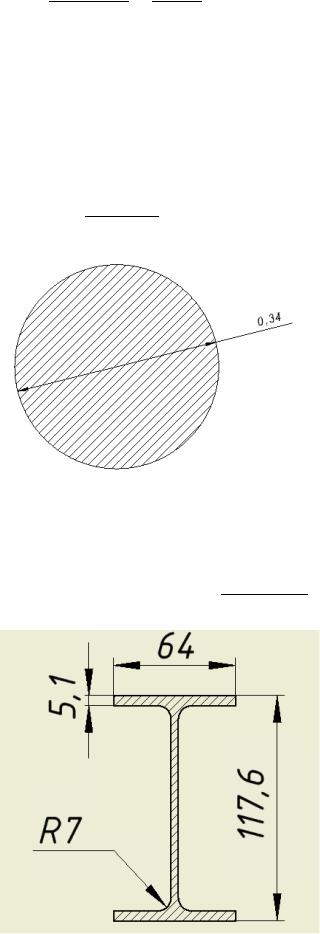
= 0.34 |
(м) |
|
|
3.14 |
|
||||
|
|
|
|
|
[ ] = 600∙103∙32 = 155.6 МПа
3.14∙(0.34)3
Согласно ГОСТ 26020-83 выберем двутавр номер профиля 12Б1, для которого h=117.6 мм, b=64 мм, s=3.8 мм, t=5.1 мм, r=7 мм, А=11,03 см2, Wx=43.8 см3.
600 ∙ 103= 43,8 ∙ 10−4 = 136,9 МПа ≤ [ ]
