

1
КЛАСТЕРНЫЙ АНАЛИЗ
2
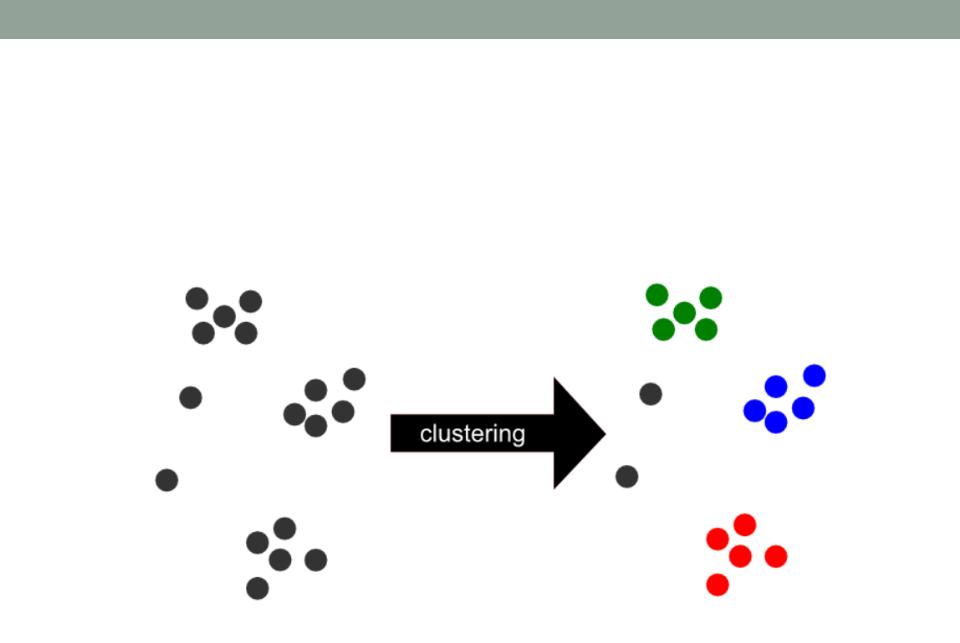
Кластерный анализ
Многомерная статистическая процедура:
•Сбор данных
•Упорядочивание
• Статистическая обработка
• Обучения без учителя

3
Обучение без учителя
Испытуемая система спонтанно обучается выполнять поставленную задачу без вмешательства со стороны экспериментатора.
•Известны описания множества объектов (обучающей выборки)
•Требуется обнаружить внутренние взаимосвязи, зависимости, закономерности, существующие между объектами.

4
История
Термин «кластерный анализ» (англ. cluster — гроздь, сгусток, пучок) предложен математиком Р. Трионом.

5
Особенности
Использование:
•Археология
•Медицина
•Психология
•Химия
•Биология
•Государственное управление
•Филология
•Антропологии
•Маркетинге
•Социология
•Геология и др.
Достоинство
•Разбиение объектов по ряду признаков
•Не накладывает ограничения на вид объектов
•Позволяет исследовать множество исходных данных произвольной природы.

6
Идея и задача
Кластеры – это группы однородности Задача кластерного анализа:
•Разбить множество на m кластеров
•Каждый объект принадлежит только одному кластеру
•Объекты одного кластера однородные (сходными)
•Объекты разных кластеров – разнородные

7
Метрики
• |
Евклидово расстояние |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
, |
= |
|
( |
|
− |
|
)2 , |
|
|
, |
|
= |
|
|
1 |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
, |
|
, |
|
|
|
|
1+ |
|
( |
− |
)2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
, |
|
|
|
•Квадрат евклидова расстояния
•Манхэттенское расстояние городских кварталов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
Косинусная мера |
|
= |
|
, |
|
, |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
, |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
∩ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
• |
Коэффициент Жаккара |
|
, |
= |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
∙ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
• |
Частные коэффициенты корреляции |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
, |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− |
2 |
1− |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
• |
Процент несогласия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
Коэффициент корреляции Пирсона |
|
|
|
|
= |
|
(, − )(, − ) |
, |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
− |
)2 |
|
|
|
( |
|
− )2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
, |
|
|
|
|||||

8
Методы
Вероятностный подход. Предполагается, что каждый рассматриваемый объект относится к одному из k кластеров.
•K-средних
•К-медиан
•EM-алгоритм
•Алгоритмы семейства FOREL
•Дискриминантный анализ

9
Методы
Подходы на основе систем искусственного интеллекта:
•Метод нечеткой кластеризации C-средних (C-means)
•Нейронная сеть Кохонена
•Генетический алгоритм

10
Методы
•Логический подход. Построение дендрограммы осуществляется с помощью дерева решений.
•Графовые алгоритмы кластеризации
•Иерархический подход. Предполагается наличие вложенных групп (кластеров различного порядка).
•Другие методы.
