2. Анализ цепи операторным методом при апериодическом воздействии

1. Определение функции передачи HU(s) = Uн(s) / U0(s)

Функция передачи определяется для цепи, представленной на рис. 2.1, методом пропорциональных величин:

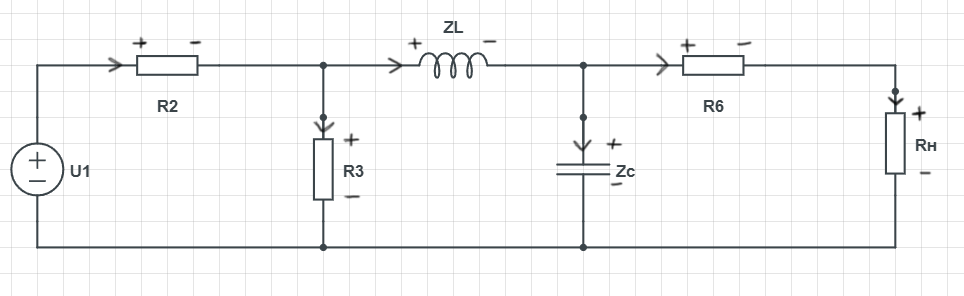
Рис. 2.1

Исходные данные:

Z_C = 1 / CS = 20 / S; Z_L = LS = 0,03S; R_н = 1; R₂ = R₆ = 0,5; R₃ = 4;

Пусть:

I’n = 1 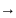U’n = 1; I’6 = I’n = 1 U’₆ = 0,5;

U’_C = U’₆ + U’_n = 1,5 I’_C = 1,5 / (20 / S) = 3S / 40;

I’_L = I’₆ + I’_C = 1 + (3S / 40); U’_L = (1 + 3S / 40) * 0,03S = (120S + 9S²) / 4000;

U’₃ = U’_L + U’_C = (120S + 9S²) / 4000 + 1,5 = (120S + 9S² + 6000) / 4000;

I’₃ = (9S² + 120S + 6000) / 16000;

I’₂­ = I’_L + I’₃ = 1 + (3S / 40) + (9S² + 120S + 6000) / 16000 =

= (9S² + 1320S + 22000) / 16000; U’₂ = (9S² + 1320S + 22000) / 32000;

U’₁ = U’₂ + U’₃ = (81S² + 2280S + 70000) / 32000;

Следовательно:

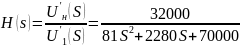
2. Определение нулей и полюсов функции передачи

H(s) = 0 при s = 0 – нуль функции передачи. Для определения полюсов функции передачи приравняем знаменатель к нулю:

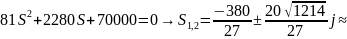
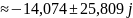
На рис. 2.2 представлено расположение на комплексной плоскости полюсов и нулей передаточной функции:

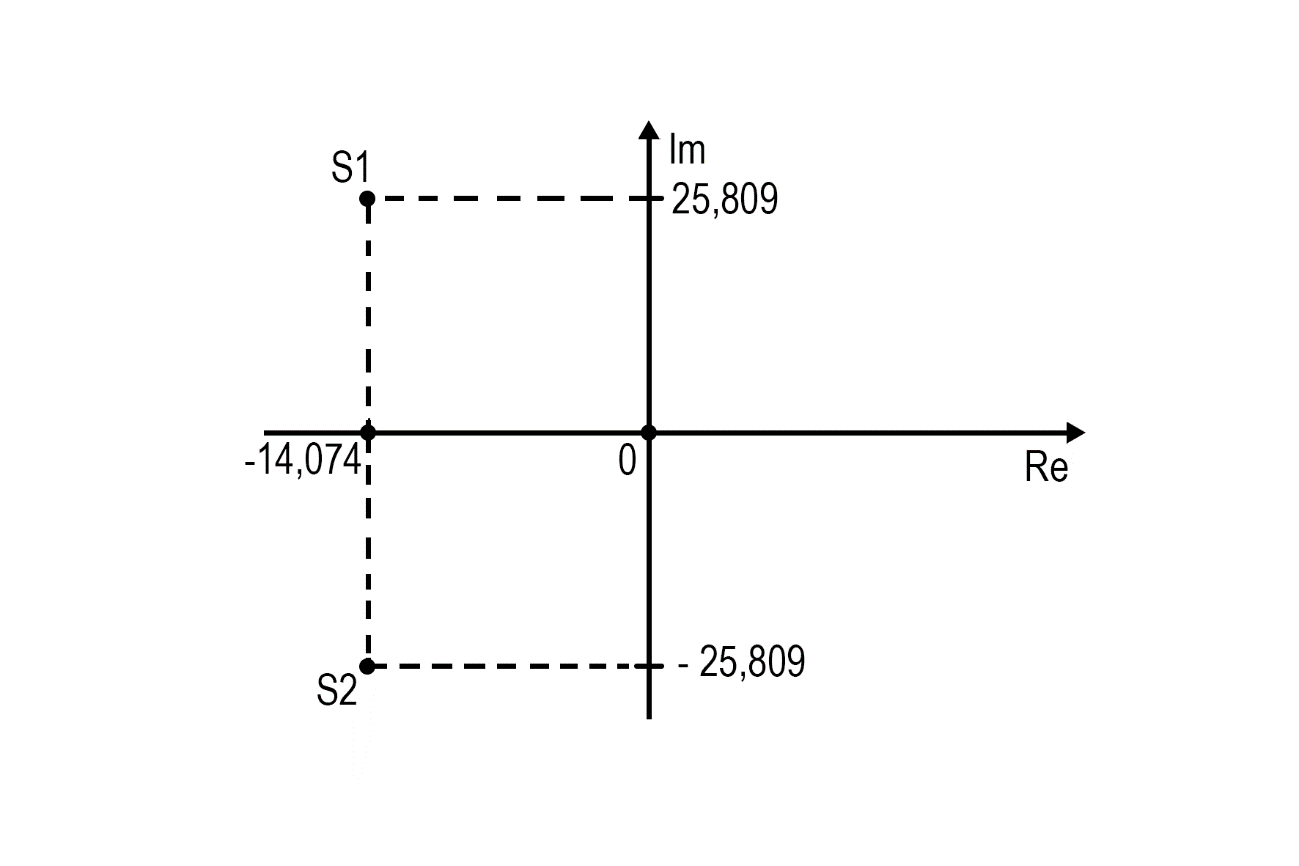
Рис. 2.2

3. Определение переходной h1(t) и импульсной h(t) характеристик для выходного сигнала

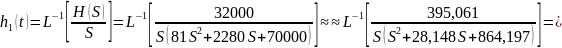
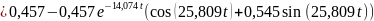
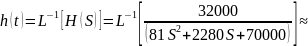
4. Определение изображения по Лапласу входного одиночного импульса

Для импульса, изображённого на рис. 2.3, оригинал входного напряжения:

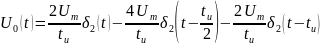
Рис. 2.3

Первая и вторая производные от данного импульса представлены на рисунках 2.4, 2.5.

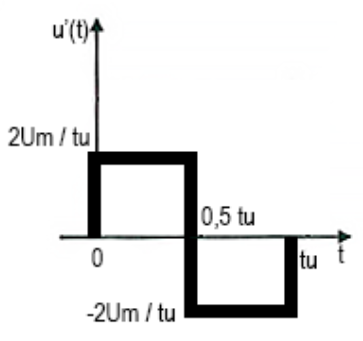
Рис. 2.4

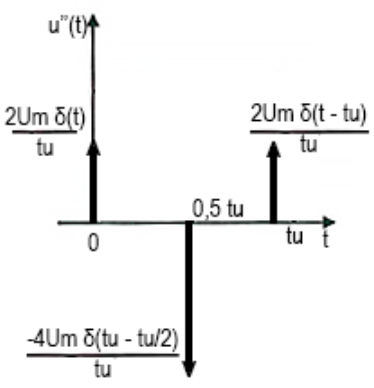
Рис. 2.5

Тогда изображение по Лапласу:

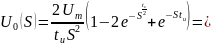
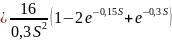
5. Определение напряжения Uн (t) на выходе цепи, используя функцию передачи H(s)

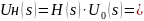
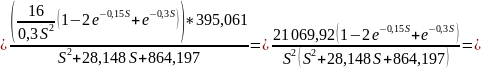
6. Построение графиков переходной и импульсной характеристик цепи, а также входного и выходного сигналов

На рис. 2.6 и 2.7 показаны графики переходной, импульсной характеристик и входного, выходного сигналов соответственно:

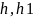
Рис. 2.6

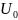
Рис. 2.7

3. КАЧЕСТВЕННЫЙ АНАЛИЗ ЦЕПИ ЧАСТОТНЫМ МЕТОДОМ ПРИ АПЕРИОДИЧЕСКОМ ВОЗДЕЙСТВИИ.

1. Нахождение и построение АФХ, АЧХ и ФЧХ функции передачи цепи

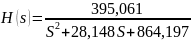
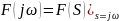
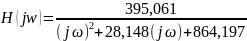
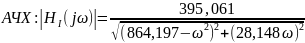
График АЧХ представлен на рис. 3.1

Рис. 3.1

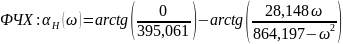
График ФЧХ представлен на рис. 3.2

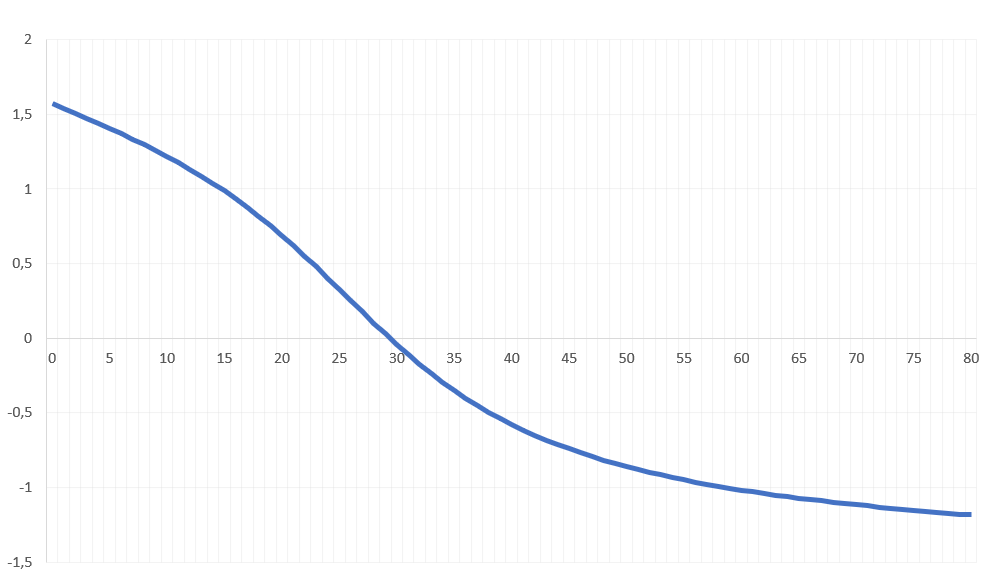
Рис. 3.2

Im

График АФХ представлен на рис. 3.3:

Re

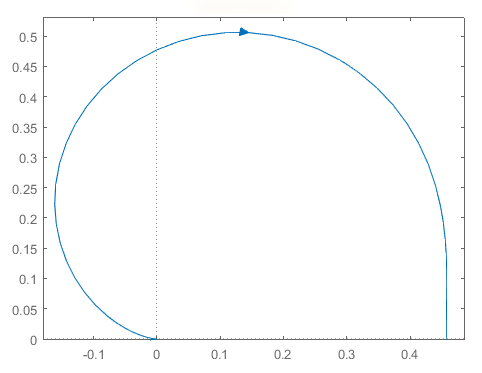
Рис. 3.3

2. Определение полосы пропускания цепи по уровню 0,707|H(jω)|_max

Из графика АЧХ, представленного на рис. 3.1:

|H(jω)| → |H(jω)|_max ≈ 0,55

при ω → ∞, 0,707|H(jω)|_max ≈ 0,707 ‧ 0,55 ≈ 0,388

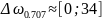
3. Нахождение и построение амплитудного и фазового спектров апериодического входного сигнала и определение ширины спектра по уровню 0,1|F(jω)|_max

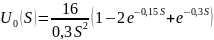
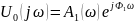
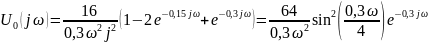
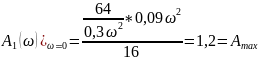
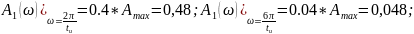
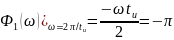
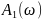
Графики спектров A₁(ω) и Ф₁(ω) представлены на рис. 3.4 и 3.5 соответственно:

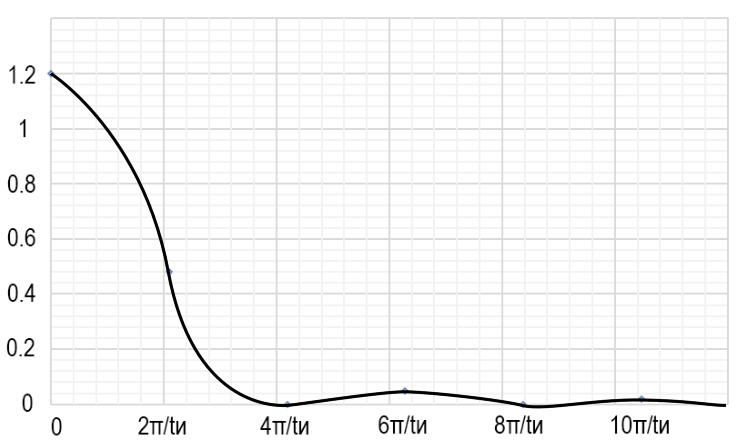
Рис. 3.4

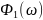
(неправильно. От 2pi/tu до конца повторяется то, что от 0 до 2pi/tu)

Рис. 3.5

Из графика на рис. 3.4 ширина спектра, определённая по 10%-ому критерию, ∆ω_пп ≈ [0; 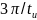] ≈ [0; 31,4].

4. Заключение об ожидаемых искажениях сигнала на выходе цепи.

Сопоставляя спектры входного сигнала (рис. 3.4 и рис. 3.5) с частотными характеристиками цепи (рис. 3.1, рис. 3.2, рис 3.3), можно установить, что приблизительно одна десятая часть амплитудного спектра входного сигнала укладывается в полосу пропускания. Таким образом, при прохождении через цепь входной сигнал будет в значительной степени искажен. На выходе цепи можно ожидать сигнал, значительно более слабый, чем поданный на вход, и более выраженный по своей продолжительности. Этот качественный вывод подтверждается точным расчетом в п.2 (см. рис. 2.7).